2020八年级数学上册第十三章轴对称13

2020八年级数学上册第十三章轴对称13

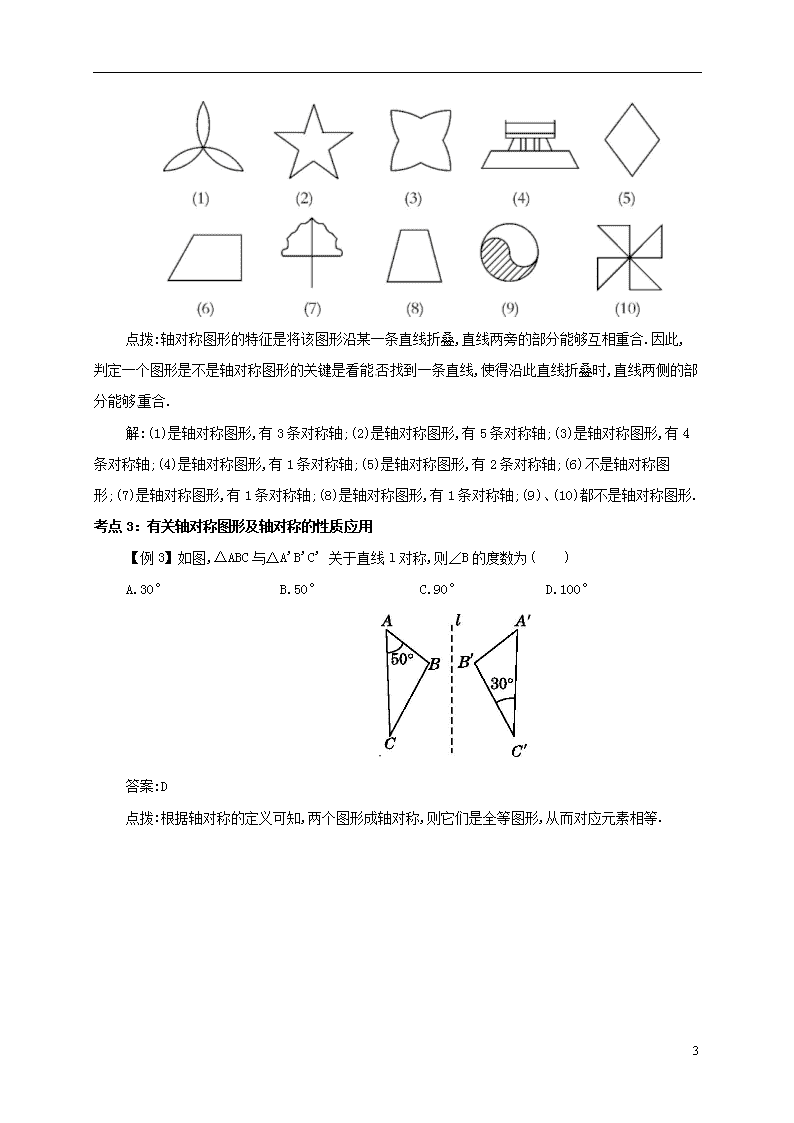
第十三章 ‎13.1.1‎轴对称 知识点1：轴对称图形的概念 ‎ 如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的一条对称轴.‎ 注意：(1)轴对称图形的对称轴不一定有一条,对称轴可以有2条,3条,4条……甚至无数条.如圆是轴对称图形,对称轴有无数条; (2)轴对称图形的对称轴是一条直线,而不是线段; (3)轴对称图形是一个图形本身的特殊性质,沿对称轴折叠后,两个部分互相重合.‎ 知识点2：轴对称的概念 ‎ 把一个图形沿某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.‎ 归纳整理:轴对称图形和轴对称的区别与联系.‎ 区别:(1)轴对称涉及两个图形,而轴对称图形是对一个图形而言的;(2)轴对称是描述的两个图形的位置关系,而轴对称图形则是一个具有特殊形状的图形.‎ 联系:(1)两个定义中都有沿某条直线折叠后重合这一条件;(2)一个轴对称图形被对称轴分成轴对称的两个图形;反之,把成轴对称的两个图形看做一个整体时,则该图形就是轴对称图形.‎ 知识点3：轴对称及轴对称图形的性质 ‎ ‎(1)如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.‎ ‎(2)轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.‎ 注意：(1)成轴对称的两个图形的对应线段相等,对应角相等. (2)成轴对称的两个图形是全等形;轴对称图形被对称轴分成的两部分也全等,但全等的两个图形不一定是轴对称图形. 如图所示:△ABC与△‎ 3‎ A'B'C'关于直线MN对称,此时A与A',B与B',C与C'是对称点.沿直线MN折叠后A与A',B与B',C与C'互相重合,则有对应边相等,对应角相等.                        ‎ 考点1：对轴对称图形的认识 ‎【例1】如图,在由小正方形组成的L形图中,请你用三种方法分别在图中添画一个小正方形,使它成为轴对称图形.‎ 解:根据图中三个图形的特征,利用轴对称的知识可以得到如图13.1-14所示的补充后的轴对称图形.‎ 点拨:本题不同于直接作出一个图形的轴对称图形,而是需要先找准对称轴,然后才能把轴对称图形补充完整.‎ 考点2：轴对称图形的对称轴 【例1】找出图中的轴对称图形,并说出有几条对称轴.‎ 3‎ 点拨:轴对称图形的特征是将该图形沿某一条直线折叠,直线两旁的部分能够互相重合.因此,判定一个图形是不是轴对称图形的关键是看能否找到一条直线,使得沿此直线折叠时,直线两侧的部分能够重合.‎ 解:(1)是轴对称图形,有3条对称轴;(2)是轴对称图形,有5条对称轴;(3)是轴对称图形,有4条对称轴;(4)是轴对称图形,有1条对称轴;(5)是轴对称图形,有2条对称轴;(6)不是轴对称图形;(7)是轴对称图形,有1条对称轴;(8)是轴对称图形,有1条对称轴;(9)、(10)都不是轴对称图形.‎ 考点3：有关轴对称图形及轴对称的性质应用 ‎【例3】如图,△ABC与△A'B'C' 关于直线l对称,则∠B的度数为(　　)‎ A.30°         B.50°        C.90°       D.100°‎ ‎                  ‎ 答案:D 点拨:根据轴对称的定义可知,两个图形成轴对称,则它们是全等图形,从而对应元素相等.‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 3‎