- 2021-04-12 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
《同步课时卷》北师版八年级数学(下册)6
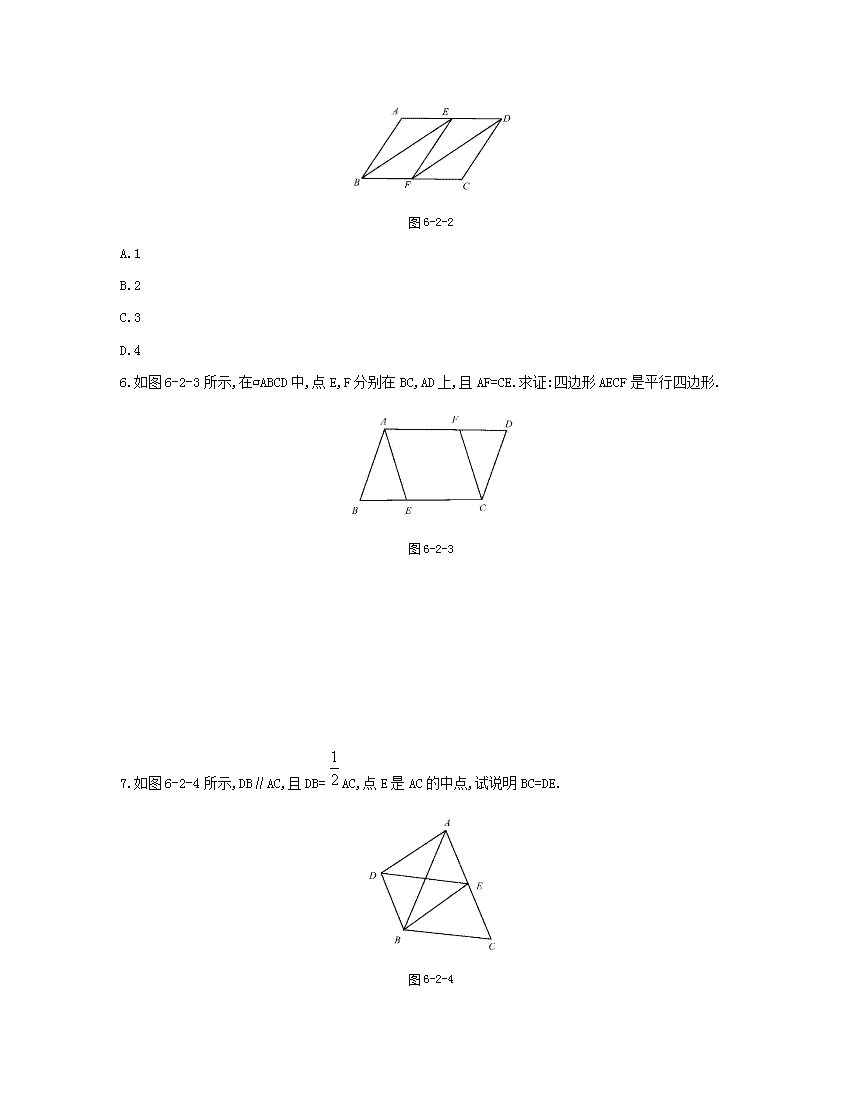
《同步课时卷》北师版八年级数学(下册) 6.2平行四边形的判定(第一课时) 1.A,B,C,D四点在同一平面内,从①AB∥CD;②AB=CD;③BC=AD;④BC∥AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有( ) A.3种 B.4种 C.5种 D.6种 2.如图6-2-1所示,在四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则应添加的条件是 (添加一个条件即可). 图6-2-1 3.在四边形ABCD中,AD∥BC,且AD=BC,若AB=4cm,则DC的长等于( ) A.2cm B.3cm C.4cm D.5cm 4.在四边形ABCD中,AD∥BC,要判定四边形ABCD是平行四边形,那么还需要满足( ) A.∠A+∠C=180° B.∠B+∠D=180° C.∠A+∠B=180° D.∠A+∠D=180° 5.如图6-2-2所示,在平行四边形ABCD中,点E,F分别为边AD,BC的中点,则图中平行四边形的个数是(不包括平行四边形ABCD)( ) 图6-2-2 A.1 B.2 C.3 D.4 6.如图6-2-3所示,在▱ABCD中,点E,F分别在BC,AD上,且AF=CE.求证:四边形AECF是平行四边形. 图6-2-3 7.如图6-2-4所示,DB∥AC,且DB=AC,点E是AC的中点,试说明BC=DE. 图6-2-4 8.下列条件能判定四边形ABCD为平行四边形的是( ) ①AB∥CD,AB=CD; ②AB=CD,AD=BC; ③AB=CD,AD∥BC; ④AB∥CD,AD∥BC. A.①②③ B.②③④ C.①②④ D.①③④ 9.在四边形ABCD中,AB=CD,BC=AD,若∠A=80°,则∠C= . 10.如图6-2-5,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC. 求证:四边形BFCE是平行四边形. 图6-2-5 11.如图6-2-6所示,点E,F是四边形ABCD的对角线AC上两点,已知DF∥BE,且AF=CE,DF=BE,试说明: (1)△AFD≌△CEB; (2)四边形ABCD是平行四边形. 图6-2-6 12.如图6-2-7所示,AC是平行四边形ABCD的一条对角线,BM⊥AC,DN⊥AC,垂足分别为点M,N,四边形BMDN是平行四边形吗?并说明你的理由. 图6-2-7 参考答案 1.B 2.AB=CD(答案不唯一) 3.C 4.D 5.C 6.证明:∵四边形ABCD是平行四边形, ∴AD∥BC,即AF∥CE. 又∵AF=CE, ∴四边形AECF是平行四边形. 7.证明:∵点E是AC的中点, ∴EC=AC. 又∵DB=AC, ∴EC=DB. ∵DB∥AC,即DB∥EC, ∴四边形DBCE是平行四边形. ∴BC=DE. 8.C 9.80° 10.证明:∵AB=DC, ∴AB+BC=BC+CD, ∴AC=DB. 在△AEC和△DFB中, ∴△AEC≌△DFB(SAS), ∴EC=BF,∠ACE=∠DBF, ∴EC∥BF, ∴四边形BFCE是平行四边形. 11.证明:(1)∵DF∥BE, ∴∠DFA=∠BEC. 又∵AF=CE,DF=BE, ∴△AFD≌△CEB. (2)由(1)知△AFD≌△CEB, ∴∠DAC=∠BCA,AD=BC, ∴AD∥BC. ∴四边形ABCD是平行四边形. 12.解:四边形BMDN是平行四边形.理由如下: ∵四边形ABCD是平行四边形, ∴AD=BC,AD∥BC, ∴∠DAN=∠BCM. 又∵BM⊥AC,DN⊥AC, ∴∠DNA=∠BMC=90°, ∴△AND≌△CMB,∴DN=BM. 又∵BM⊥AC,DN⊥AC, ∴DN∥BM. ∴四边形BMDN是平行四边形.查看更多