中考数学复习题折叠问题

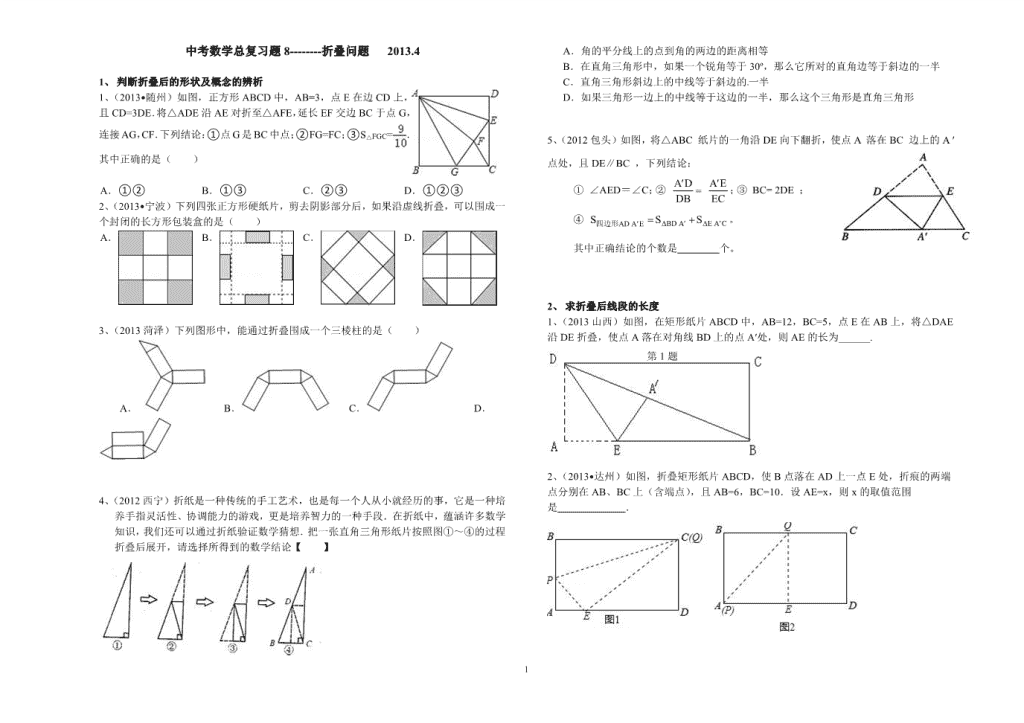
中考数学复习题折叠问题

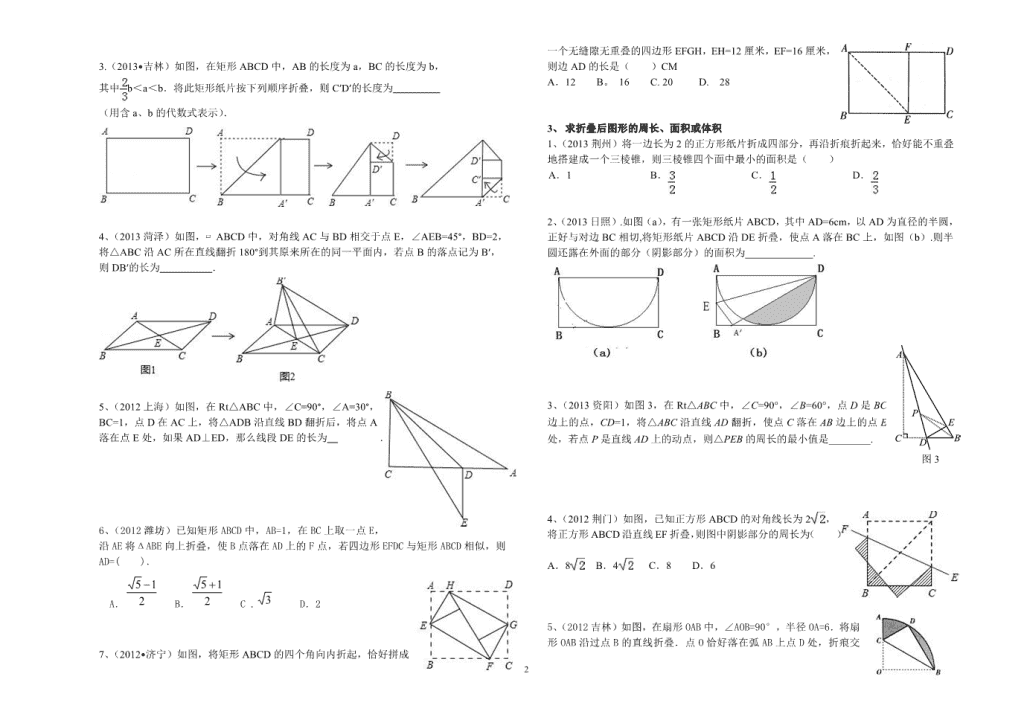
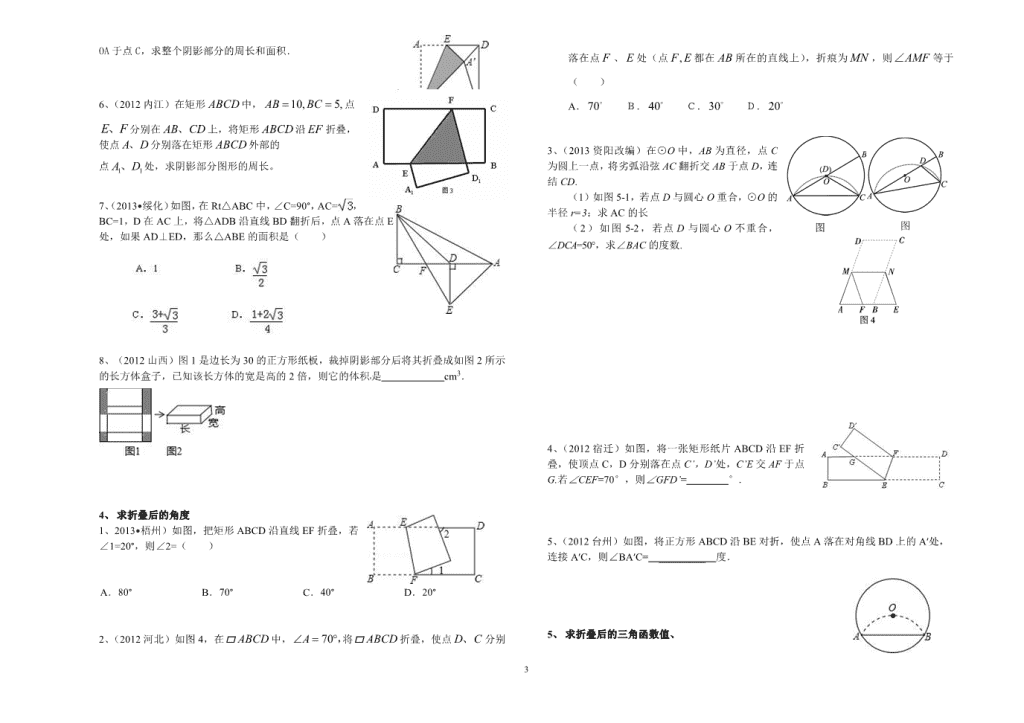
1 中考数学总复习题 8--------折叠问题 2013.4 1、 判断折叠后的形状及概念的辨析 1、（2013•随州）如图，正方形 ABCD 中，AB=3，点 E 在边 CD 上， 且 CD=3DE．将△ADE 沿 AE 对折至△AFE，延长 EF 交边 BC 于点 G， 连接 AG，CF．下列结论：①点 G 是 BC 中点；②FG=FC；③S△FGC= ． 其中正确的是（ ） A．①② B．①③ C．②③ D．①②③ 2、（2013•宁波）下列四张正方形硬纸片，剪去阴影部分后，如果沿虚线折叠，可以围成一 个封闭的长方形包装盒的是（ ） A． B． C． D． 3、（2013 菏泽）下列图形中，能通过折叠围成一个三棱柱的是（ ） A． B． C． D． 4、（2012 西宁）折纸是一种传统的手工艺术，也是每一个人从小就经历的事，它是一种培 养手指灵活性、协调能力的游戏，更是培养智力的一种手段．在折纸中，蕴涵许多数学 知识，我们还可以通过折纸验证数学猜想．把一张直角三角形纸片按照图①～④的过程 折叠后展开，请选择所得到的数学结论【 】 A．角的平分线上的点到角的两边的距离相等 B．在直角三角形中，如果一个锐角等于 30º，那么它所对的直角边等于斜边的一半 C．直角三角形斜边上的中线等于斜边的一半 D．如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形 5、（2012 包头）如图，将△ABC 纸片的一角沿 DE 向下翻折，使点 A 落在 BC 边上的 A ′ 点处，且 DE∥BC ，下列结论： ① ∠AED＝∠C；② A D A E DB EC   ；③ BC= 2DE ； ④ BD A E A CAD A ES S S     四 形边 。 其中正确结论的个数是 个。 2、 求折叠后线段的长度 1、（2013 山西）如图，在矩形纸片 ABCD 中，AB=12，BC=5，点 E 在 AB 上，将△DAE 沿 DE 折叠，使点 A 落在对角线 BD 上的点 A′处，则 AE 的长为______. 2、（2013•达州）如图，折叠矩形纸片 ABCD，使 B 点落在 AD 上一点 E 处，折痕的两端 点分别在 AB、BC 上（含端点），且 AB=6，BC=10．设 AE=x，则 x 的取值范围 是 ． 第 1 题 2 3.（2013•吉林）如图，在矩形 ABCD 中，AB 的长度为 a，BC 的长度为 b， 其中 b＜a＜b．将此矩形纸片按下列顺序折叠，则 C′D′的长度为 （用含 a、b 的代数式表示）． 4、（2013 菏泽）如图，▱ ABCD 中，对角线 AC 与 BD 相交于点 E，∠AEB=45°，BD=2， 将△ABC 沿 AC 所在直线翻折 180°到其原来所在的同一平面内，若点 B 的落点记为 B′， 则 DB′的长为 ． 5、（2012 上海）如图，在 Rt△ABC 中，∠C=90°，∠A=30°， BC=1，点 D 在 AC 上，将△ADB 沿直线 BD 翻折后，将点 A 落在点 E 处，如果 AD⊥ED，那么线段 DE 的长为 ． 6、（2012 潍坊）已知矩形 ABCD 中，AB=1，在 BC 上取一点 E， 沿 AE 将ΔABE 向上折叠，使 B 点落在 AD 上的 F 点，若四边形 EFDC 与矩形 ABCD 相似，则 AD=( )． A． 2 15  B． 2 15  C . 3 D．2 7、（2012•济宁）如图，将矩形 ABCD 的四个角向内折起，恰好拼成 一个无缝隙无重叠的四边形 EFGH，EH=12 厘米，EF=16 厘米， 则边 AD 的长是（ ）CM A．12 B。 16 C. 20 D. 28 3、 求折叠后图形的周长、面积或体积 1、（2013 荆州）将一边长为 2 的正方形纸片折成四部分，再沿折痕折起来，恰好能不重叠 地搭建成一个三棱锥，则三棱锥四个面中最小的面积是（ ） A．1 B． C． D． 2、（2013 日照）.如图（a），有一张矩形纸片 ABCD，其中 AD=6cm，以 AD 为直径的半圆， 正好与对边 BC 相切,将矩形纸片 ABCD 沿 DE 折叠，使点 A 落在 BC 上，如图（b）.则半 圆还露在外面的部分（阴影部分）的面积为_____________. 3、（2013 资阳）如图 3，在 Rt△ABC 中，∠C=90°，∠B=60°，点 D 是 BC 边上的点，CD=1，将△ABC 沿直线 AD 翻折，使点 C 落在 AB 边上的点 E 处，若点 P 是直线 AD 上的动点，则△PEB 的周长的最小值是________. 4、（2012 荆门）如图，已知正方形 ABCD 的对角线长为 2 ， 将正方形 ABCD 沿直线 EF 折叠，则图中阴影部分的周长为（ ） A．8 B．4 C．8 D．6 5、（2012 吉林）如图，在扇形 OAB 中，∠AOB=90°，半径 OA=6．将扇 形 OAB 沿过点 B 的直线折叠．点 O 恰好落在弧 AB 上点 D 处，折痕交 图 3 3 OA 于点 C，求整个阴影部分的周长和面积． 6、（2012 内江）在矩形 ABCD 中， 10, 5,AB BC  点 E F、 分别在 AB CD、 上，将矩形 ABCD 沿 EF 折叠， 使点 A D、 分别落在矩形 ABCD 外部的 点 1 1A D、 处，求阴影部分图形的周长。 7、（2013•绥化）如图，在 Rt△ABC 中，∠C=90°，AC= ， BC=1，D 在 AC 上，将△ADB 沿直线 BD 翻折后，点 A 落在点 E 处，如果 AD⊥ED，那么△ABE 的面积是（ ） 8、（2012 山西）图 1 是边长为 30 的正方形纸板，裁掉阴影部分后将其折叠成如图 2 所示 的长方体盒子，已知该长方体的宽是高的 2 倍，则它的体积是 cm3． 4、 求折叠后的角度 1、2013•梧州）如图，把矩形 ABCD 沿直线 EF 折叠，若 ∠1=20°，则∠2=（ ） A．80° B．70° C．40° D．20° 2、（2012 河北）如图 4，在 ABCD 中， 70A  ，将 ABCD 折叠，使点 D C、 分别 落在点 F 、 E 处（点 ,F E 都在 AB 所在的直线上），折痕为 MN ，则 AMF∠ 等于 （ ） A． 70 Ｂ． 40 Ｃ．30 Ｄ． 20 3、（2013 资阳改编）在⊙O 中，AB 为直径，点 C 为圆上一点，将劣弧沿弦 AC 翻折交 AB 于点 D，连 结 CD. （1）如图 5-1，若点 D 与圆心 O 重合，⊙O 的 半径 r=3；求 AC 的长 （ 2 ） 如图 5-2 ，若点 D 与圆心 O 不重合， ∠DCA=50°，求∠BAC 的度数. 4、（2012 宿迁）如图，将一张矩形纸片 ABCD 沿 EF 折 叠，使顶点 C，D 分别落在点 C’，D’处，C’E 交 AF 于点 G.若∠CEF=70°，则∠GFD’= °. 5、（2012 台州）如图，将正方形 ABCD 沿 BE 对折，使点 A 落在对角线 BD 上的 A′处， 连接 A′C，则∠BA′C= _________ 度． 5、 求折叠后的三角函数值、 图 图 4 1、如图，将半径为 2cm 的圆形纸片折叠后，圆弧恰好经过圆心 O，则 tan∠OAB 的值为 cm． 2、小明在学习“锐角三角函数”中发现，将如图所示的矩形纸片 ABCD 沿过点 B 的直线 折叠，使点 A 落在 BC 上的点 E 处，还原后，再沿过点 E 的直线折叠，使点 A 落在 BC 上的点 F 处，这样就可以求出 67.5°角的正切值是________. 3、（2012 扬州）如图，将矩形 ABCD 沿 CE 折叠，点 B 恰好落在边 AD 的 F 处．若 AB BC ＝ 2 3 ，则 tan∠DCF 的值是 ． 6、 求折叠后的线段的比值 1、（2012•南京）如图，在菱形纸片 ABCD 中，∠A=60°， 将纸片折叠，点 A、D 分别落在点 A′、D′处，且 A′D′ 经过点 B，EF 为折叠，当 D′F⊥CD 时， 的值为（ ） A． B C. D 2、（2012 广西河池）如图，在矩形 ABCD 中， AD AB> ，将矩形 ABCD 折叠，使点C 与点 A 重合，折痕为 MN ， 连结CN ．若△CDN 的面积与△CMN 的面积 比为 1︰4，则 MN BM 的值为（ ） A．2 B．4 C． 2 5 D． 2 6 3、（2012 绍兴）如图，在矩形 ABCD 中，点 E，F 分别在 BC， CD 上，将△ABE 沿 AE 折叠，使点 B 落在 AC 上的点 B′处， 又将△CEF 沿 EF 折叠，使点 C 落在 EB′与 AD 的交点 C′处．则 BC：AB 的值为 。 7、 与折叠相关的解答题 1、（2013 晋江）将矩形OABC 置于平面直角坐标系中，点 A 的 坐 标为 )4,0( ， 点 C 的 坐 标为 )0,(m )0( m ， 点 D )1,(m 在 BC 上，将矩形 OABC 沿 AD 折叠压平，使 点 B 落在坐标平面内，设点 B 的对应点为点 E . （1）当 3m 时，点 B 的坐标为 ，点 E 的坐标 为 ； （2）随着 m 的变化，试探索：点 E 能否恰好落在 x 轴上？ 若能，请求出 m 的值；若不能，请说明理由. 2、（2013•连云港）在矩形 ABCD 中，将点 A 翻折到对角线 BD 上的点 M 处，折痕 BE 交 AD 于点 E．将点 C 翻折到对角线 BD 上的点 N 处，折痕 DF 交 BC 于点 F． （1）求证：四边形 BFDE 为平行四边形； （2）若四边形 BFDE 为为菱形，且 AB=2，求 BC 的长． y E C D B O A x (图 9) 第 2 题图 5 3、（2013•绵阳）如图，已知矩形 OABC 中，OA=2，AB=4，双曲线 （k＞0）与矩形 两边 AB、BC 分别交于 E、F． （1）若 E 是 AB 的中点，求 F 点的坐标； （2）若将△BEF 沿直线 EF 对折，B 点落在 x 轴上的 D 点，作 EG⊥OC，垂足为 G，证明 △EGD∽△DCF，并求 k 的值． 4、（2012 天津）已知一个矩形纸片 OACB，将该纸片放置在平面直角坐标洗中，点 A（11， 0），点 B（0，6），点 P 为 BC 边上的动点（点 P 不与点 B、C 重合），经过点 O、P 折叠该 纸片，得点 B′和折痕 OP．设 BP=t． （Ⅰ）如图①，当∠BOP=30°时，求点 P 的坐标； （Ⅱ）如图②，经过点 P 再次折叠纸片，使点 C 落在直线 PB′上，得点 C′和折痕 PQ， 若 AQ=m，试用含有 t 的式子表示 m； （Ⅲ）在（Ⅱ）的条件下，当点 C′恰好落在边 OA 上时，求点 P 的坐标（直接写出结果 即可）． 5、（2013•成都）如图，A，B，C 为⊙O 上相邻的三个 n 等分点， = ， 点 E 在 上，EF 为⊙O 的直径，将⊙O 沿 EF 折叠，使点 A 与 A′重合， 点 B 与 B′重合，连接 EB′，EC，EA′．设 EB′=b，EC=c，EA′=p．现探 究 b，c，p 三者的数量关系：发现当 n=3 时，p=b+c．请继续探究 b，c， p 三者的数量关系：当 n=4 或 12 时，求 p 的值； （参考数据： ， ） 6、（2013 鄂州）（本题满分 12 分）在平面直角坐标系中，已知 M1（3，2），N1（5，－1）， 线段 M1N1 平移至线段 MN 处（注：M1 与 M，N1 与 N 分别为对应点）. （1）若 M（－2，5），请直接写出 N 点坐标. （2）在（1）问的条件下，点 N 在抛物线 21 2 3 6 3y x x k   上，求该抛物线对应的函 数解析式. （3）在（2）问条件下，若抛物线顶点为 B，与 y 轴交于点 A，点 E 为线段 AB 中点，点 C（0，m）是 y 轴负半轴上一动点，线段 EC 与线段 BO 相交于 F， 且 OC︰OF=2︰ 3 ，求 m 的值. （4）在（3）问条件下，动点 P 从 B 点出发，沿 x 轴正方向匀速运动，点 P 运动到什么 6 位置时（即 BP 长为多少），将△ABP 沿边 PE 折叠，△APE 与△PBE 重叠部分的面积 恰好为此时的△ABP 面积的 1 4 ，求此时 BP 的长度. （第 6 题图） 7、（2012 南昌）已知，纸片⊙O 的半径为 2，如图 1，沿弦 AB 折叠操作． （1）①折叠后的 所在圆的圆心为 O′时，求 O′A 的长度； ②如图 2，当折叠后的 经过圆心为 O 时，求 的长度； ③如图 3，当弦 AB=2 时，求圆心 O 到弦 AB 的距离； （2）在图 1 中，再将纸片⊙O 沿弦 CD 折叠操作． ①如图 4，当 AB∥CD，折叠后的 与 所在圆外切于点 P 时，设点 O 到弦 AB．CD 的 距离之和为 d，求 d 的值； ②如图 5，当 AB 与 CD 不平行，折叠后的 与 所在圆外切于点 P 时，设点 M 为 AB 的 中点，点 N 为 CD 的中点，试探究四边形 OMPN 的形状，并证明你的结论．