- 2021-04-12 发布 |
- 37.5 KB |
- 7页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
小学数学精讲教案4_1_1几何图形的认识 学生版
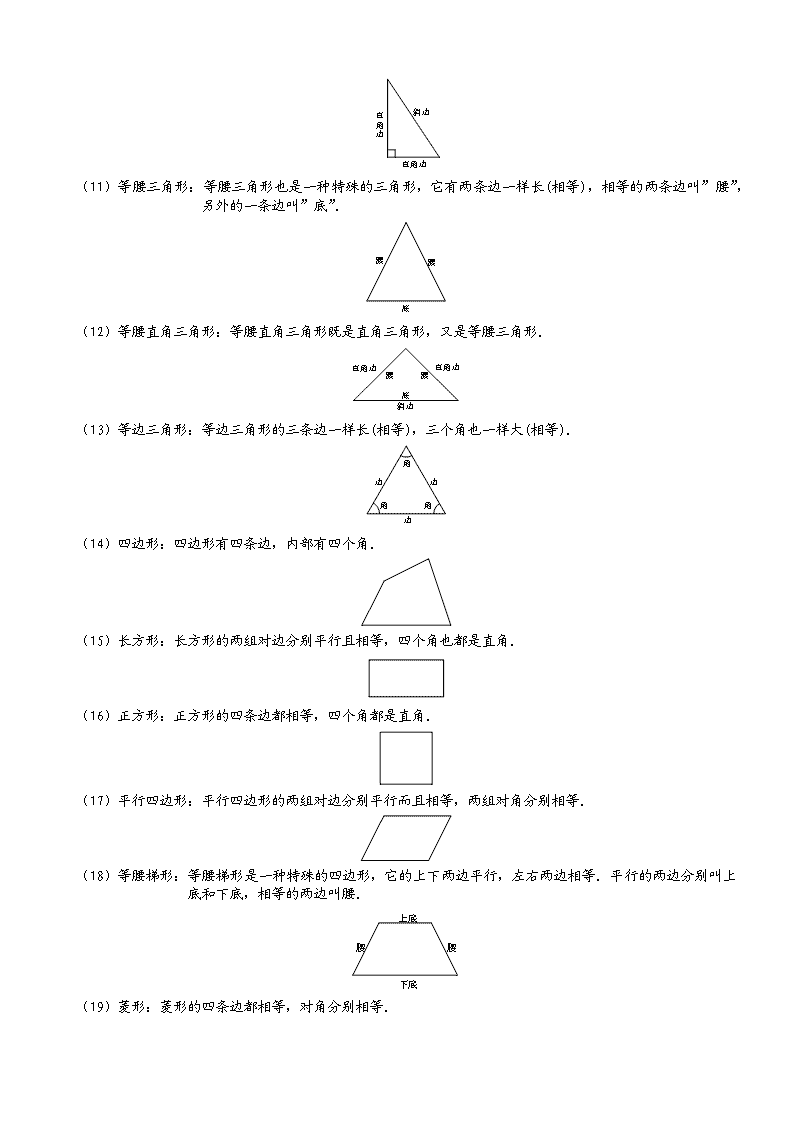
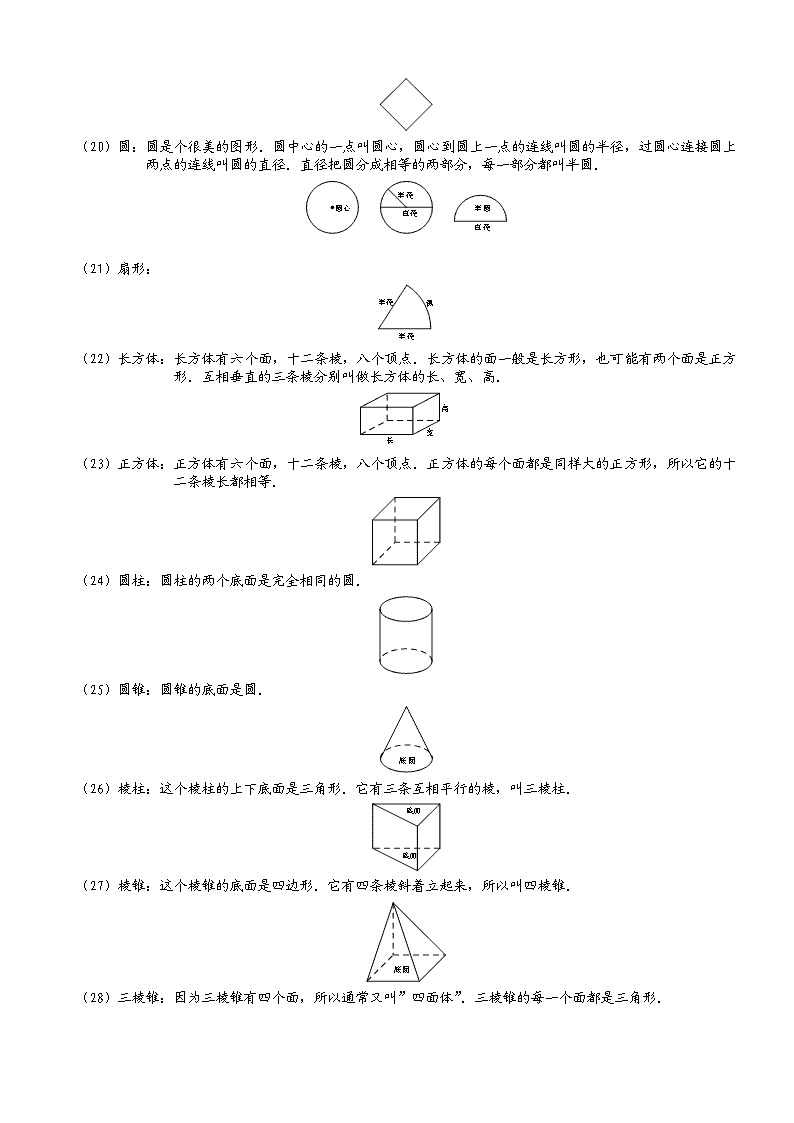
4-1-1.几何图形认知及简单计算 知识点拨 本讲知识点属于几何模块的第一讲,属于起步内容,难度并不大.要求学生认识各种基本平面图形和立体图形;了解简单的几何图形简拼和立体图形展开;看懂立体图形的示意图,锻炼一定的空间想象能力. 几何图形的定义: 1、几何图形主要分为点、线、面、体等,他们是构成中最基本的要素. (1)点:用笔在纸上画一个点,可以画大些,也可以画小些.点在纸上占一个位置. (2)线段:沿着直尺把两点用笔连起来,就能画出一条线段.线段有两个端点. (3)射线:从一点出发,沿着直尺画出去,就能画出一条射线.射线有一个端点,另一端延伸的很远很远,没有尽头. (4)直线:沿着直尺用笔可以画出直线.直线没有端点,可以向两边无限延伸 (5)两条直线相交: 两条直线相交,只有一个交点. (6)两条直线平行:两条直线平行,没有交点,无论延伸多远都不相交. (7)角:角是由从一点引出的两条射线构成的.这点叫角的顶点,射线叫点的边. (8)角分为锐角、直角和钝角三种:直角的两边互相垂直,三角板有一个角就是这样的直角. 教室里天花板上的角都是直角. 锐角比直角小,钝角比直角大. (9)三角形:三角形有三条边,三个角,三个顶点. (10)直角三角形:直角三角形是一种特殊的三角形,它有一个角是直角.它的三条边中有两条叫直角边,一条叫斜边. (11)等腰三角形:等腰三角形也是一种特殊的三角形,它有两条边一样长(相等),相等的两条边叫”腰”,另外的一条边叫”底”. (12)等腰直角三角形:等腰直角三角形既是直角三角形,又是等腰三角形. (13)等边三角形:等边三角形的三条边一样长(相等),三个角也一样大(相等). (14)四边形:四边形有四条边,内部有四个角. (15)长方形:长方形的两组对边分别平行且相等,四个角也都是直角. (16)正方形:正方形的四条边都相等,四个角都是直角. (17)平行四边形:平行四边形的两组对边分别平行而且相等,两组对角分别相等. (18)等腰梯形:等腰梯形是一种特殊的四边形,它的上下两边平行,左右两边相等.平行的两边分别叫上底和下底,相等的两边叫腰. (19)菱形:菱形的四条边都相等,对角分别相等. (20)圆:圆是个很美的图形.圆中心的一点叫圆心,圆心到圆上一点的连线叫圆的半径,过圆心连接圆上两点的连线叫圆的直径.直径把圆分成相等的两部分,每一部分都叫半圆. (21)扇形: (22)长方体:长方体有六个面,十二条棱,八个顶点.长方体的面一般是长方形,也可能有两个面是正方形.互相垂直的三条棱分别叫做长方体的长、宽、高. (23)正方体:正方体有六个面,十二条棱,八个顶点.正方体的每个面都是同样大的正方形,所以它的十二条棱长都相等. (24)圆柱:圆柱的两个底面是完全相同的圆. (25)圆锥:圆锥的底面是圆. (26)棱柱:这个棱柱的上下底面是三角形.它有三条互相平行的棱,叫三棱柱. (27)棱锥:这个棱锥的底面是四边形.它有四条棱斜着立起来,所以叫四棱锥. (28)三棱锥:因为三棱锥有四个面,所以通常又叫”四面体”.三棱锥的每一个面都是三角形. (29)球体,简称球:球有球心,球心到球面上一点的连线叫球的半径. 例题精讲 模块一、几何图形的认识 【例 1】 请看下图,共有 个圆圈。 【例 2】 下图中哪些是三角形?哪些是长方形?哪些是平行四边形?哪些是菱形? 【例 3】 数一数,图中共有多少个角? 【例 4】 长方形有四个角,剪掉一个角,还剩几个角? 【例 5】 如下图,将正方形纸片由下往上对折,再由左向右对折,称为完成一次操作.按上述规则完成五次操作以后,剪去所得小正方形的左下角.问:当展开这张正方形纸片后,共有多少个小洞孔? 模块二、几何图形的简单组合 【例 1】 一个等腰三角形的两条边的长度分别是3和4,那么这个三角形的周长可能是多少?另外一个等腰三角形的两条边的长度分别是4和9,这个三角形的周长可能是多少? 【巩固】 周长是12,各边长都是整数的等腰三角形有几种?长方形有几种? 【巩固】 用7根长度都是1寸的火柴棍拼成了一个三角形.请问:这个三角形的三条边长分别是多少? 【例 2】 有两个相同的直角三角形纸片,三条边分别为3厘米、4厘米、5厘米.不许折叠,用这两个直角三角形可以拼成几种平行四边形? 【巩固】 用两个完全相同的、各边长分别为5、12、13的直角三角形纸片,可以拼成多少种不同的平行四边形? 【例 3】 用12个边长为1的小正方形拼一个大长方形,这个长方形的周长最短是多少? 【例 4】 把一个正方形分割为三种面积不同的小正方形,并且小正方形的个数是8.如何分? 【例 5】 一个正方体的8个顶角被截去后,得到一个新的几何体.这个新的几何体有几个面?几个顶点?几条棱? 模块三、基本图形的周长及面积计算 【例 1】 一个正方形的面积和它的周长的数值相等,那么这个正方形的边长是__________ 【例 2】 正方形的一条对角线长13厘米,这个正方形的面积是 平方厘米。 【例 3】 用20厘米长的铜丝弯成边长是整数的长方形,这样的长方形不只一种。其中,面积最小的,长______ 厘米,宽______ 厘米;面积最大的长______ 厘米,宽______ 厘米。 【例 4】 在长方形ABCD中,,,那么△AEF的面积是________. 【例 5】 右图中平行四边形的面积是,则平行四边形的周长为__________. 【例 6】 如图,平行四边形ABCD被分成三角形ADF和梯形ABCF两部分,它们的面积相差14平方厘米,已知AE=7厘米,那么FC=___________厘米。 【例 7】 有三条线段、、,米,米,米,以它们作为上底、下底和高,可以作出三个不同的梯形.问:第几个梯形的面积最大(如下图)? 【例 1】 如图2,三个图形的周长相等,则a:b:c=___________________。 【巩固】 如图,三个图形的周长相等,则a:b:c= 。 查看更多