人教版九年级上册数学同步练习课件-第24章 圆-24 圆周角

人教版九年级上册数学同步练习课件-第24章 圆-24 圆周角

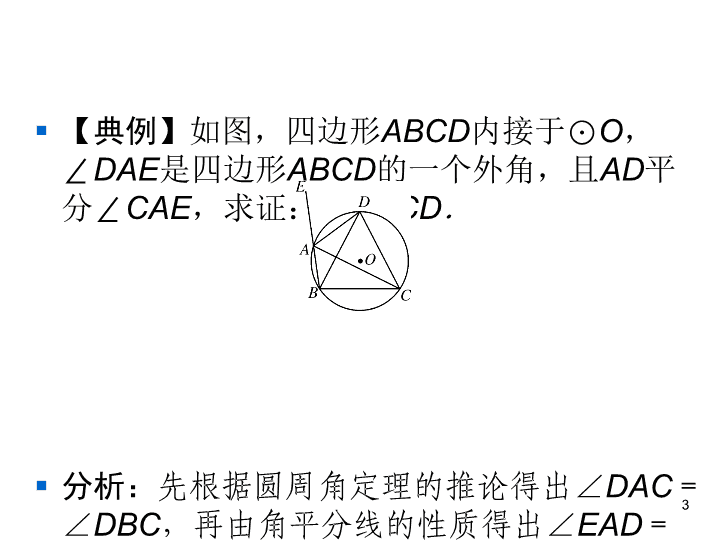
第二十四章　圆 24.1　圆的有关性质 24.1.4　圆周角 第五课时　圆内接四边形的性质 § 知识点1　圆内接多边形 § 如果一个多边形的所有顶点都在同一个圆上， 这个多边形叫做圆内接多边形，这个圆叫做 多边形的外接圆． § 知识点2　圆内接四边形的性质 § 圆内接四边形的对角互补． § 提示：由圆内接四边形的性质，可以很容易 得到一个推论：圆内接四边形的一个外角等 于它的内对角．这个推论在解题中的应用非 常广泛，虽然它不能作为定理直接应用，但 它能帮助我们迅速理清解题思路． 2 § 【典例】如图，四边形ABCD内接于⊙ O， ∠DAE是四边形ABCD的一个外角，且AD平 分∠CAE，求证：BD＝CD． § 分析：先根据圆周角定理的推论得出∠DAC ＝∠DBC，再由角平分线的性质得出∠EAD ＝∠DAC，最后根据圆内接四边形的性质得 出∠EAD＝∠BCD，由此可得出结论． 3 § 证明：∵∠DAC与∠DBC是同弧所对的圆周 角， § ∴∠DAC＝∠DBC． § ∵AD平分∠CAE， § ∴∠EAD＝∠DAC， § ∴∠EAD＝∠DBC． § ∵四边形ABCD内接于⊙O， § ∴∠DAB＋∠BCD＝180°. § 又∵∠EAD＋∠DAB＝180°， § ∴∠EAD＝∠BCD， § ∴∠DBC＝∠DCB， § ∴BD＝CD． 4 § 点评：在理解“圆内接四边形对角互补”的 性质时，应首先理解“互补”的概念，实际 上，“互补”是指两个角之间的一种特殊的 数量关系，而不是位置关系，只要两个角的 度数之和等于180°，则这两个角就一定互 补． 5 § 1．圆内接四边形ABCD中，已知∠A＝70°， 则∠C＝ (　　) § A．20°　 B．30°　 § C．70°　 D．110° 6 D　 § 2．【2018·湖南邵阳中考】如图所示，四边 形ABCD为⊙ O的内接四边形，∠BCD＝ 120°，则∠BOD的大小是 (　　) § A．80°　 B．120°　 § C．100°　 D．90° 7 B　 § 3．【辽宁锦州中考】如图，四边形ABCD是 ⊙ O的内接四边形，AD与BC的延长线交于点 E，BA与CD的延长线交于点F，∠DCE＝ 80°，∠F＝25°，则∠E的度数为 (　　) § A．55°　 B．50°　 § C．45°　 D．40° 8 C　 § 4．如图，AB为⊙ O的直径，点C、D在⊙ O 上．若∠AOD＝30°，则∠BCD的度数是 (　　) § A．150°　 B．120°　 § C．105°　 D．75° 9 C　 § 5．【2018·云南曲靖中考】如图，四边形 ABCD内接于⊙ O，E为BC延长线上一点， 若∠A＝n°，则∠DCE＝______°. 10 n　 § 6．如图，在⊙ O中，∠AOC＝140°， ∠ACB＝50°，则∠BAC＝________. 11 20°　 § 7．如图，四边形ABCD内接于⊙ O，AB、 DC的延长线相交于点E，AD、BC的延长线 相交于点F，若∠A＝45°，∠E＝40°，则 ∠F的度数为________. 12 50°　 § 8．如图，四边形ABCD内接于⊙ O， 点E在对角线AC上，EC＝BC＝ DC． § (1)若∠CBD＝39°，求∠BAD的度 数； § (2)求证：∠1＝∠2. 13 (1)解：∵BC＝DC，∴∠CDB＝∠CBD＝39°.∵∠BAC＝∠CDB＝39°， ∠CAD＝∠CBD＝39°，∴∠BAD＝∠BAC＋∠CAD＝39°＋39°＝78°.　(2)证 明：∵EC＝BC，∴∠CEB＝∠CBE.又∠CEB＝∠2＋∠BAE，∠CBE＝∠1＋ ∠CBD，∴∠2＋∠BAE＝∠1＋∠CBD．由(1)得∠BAE＝∠CBD，∴∠1＝∠2.