2020版六年级数学下册六正比例和反比例6

2020版六年级数学下册六正比例和反比例6

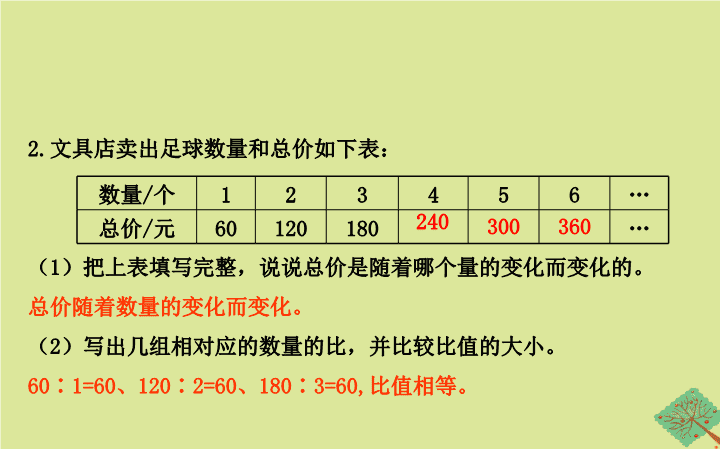
六 正比例和反比例 1. 认识成正比例的量 【 对点训练 】 1. 填一填。 （ 1 ）成正比例的两种量的（ ）是一定的。 （ 2 ） =c （一定）， a 和 b 成（ ）关系。 比值 正比例 2. 文具店卖出足球数量和总价如下表： （ 1 ）把上表填写完整，说说总价是随着哪个量的变化而变化的。 总价随着数量的变化而变化。 （ 2 ）写出几组相对应的数量的比，并比较比值的大小。 60∶1=60 、 120∶2=60 、 180∶3=60, 比值相等。 数量 / 个 1 2 3 4 5 6 … 总价 / 元 60 120 180 … 240 300 360 （ 3 ）这个比值表示的意义是什么？你能用式子表示它与总价和数量之间的关系吗？ 这个比值表示的意义是单价， = 单价（一定） （ 4 ）足球的总价和数量成正比例吗？为什么？ 成正比例，总价和数量是相关联的两个量，且比值一定，所以成正比例关系。 3. 订购一份报纸的份数和应付钱数如下表。 （ 1 ）图中份数和应付钱数是成正比例的量，试着把表格填写完整。 份数 5 10 20 30 40 50 应付钱数 / 元 2.5 5 10 15 20 25 （ 2 ）在图中描出份数和应付钱数所对应的点，再按顺序连接起来。 （ 3 ）根据图像判断，买 25 份报纸需要多少元钱？ 付出 17.5 元可以买多少份报纸？ 根据图像判断，买 25 份报纸需要付 12.5 元， 付 17.5 元可以买 35 份报纸。 教材练习十 P59 T2 先分别按 2:1 、 3:1 和 4:1 的比画出正方形放大后的图形，再填写下表。分析观察，正方形的周长与边长成正比例吗？为什么？面积与边长呢？ 【 示范解答 】 正方形的周长与边长的比值分别是 4 、 4 、 4 、 4 ，所以正方形的周长与边长成正比例关系； 正方形的面积与边长的比值分别是 1 、 2 、 3 、 4 ，所以正方形的面积与边长不成正比例关系。 运用公式法巧解正比例问题 判断下面各题中的两种量是否成正比例。 （ 1 ）长方形的面积一定，长方形的长和宽。（ ） （ 2 ）人的年龄和身高。（ ） （ 3 ）正方体的体积和底面积。（ ） （ 4 ）三角形的底一定，三角形的面积和高。（ ） 【 示范解答 】 （ 1 ）不成比例。由长方形的面积公式： S=ab ，可知长方形的长和宽是相乘的关系，不能写成比的形式，所以不成正比例关系。 （ 2 ）不成比例。人的年龄和身高没有一定的公式关系。 （ 3 ）不成比例。由正方体的体积公式 V=Sh, 可知 =S ，而正方体的高也就是棱长不是定值，所以不成比例。 （ 4 ）成正比例。由三角形的面积公式 S= ah ，可知 （一定），三角形的面积和高可以写成相比的形式，比值一定，所以成正比例。 【 对点训练 】 4. 判断下面各题中的两种量是否成正比例，并说出原因。 （ 1 ）工作总量一定，工作效率和工作时间。 不成正比例，工作效率 × 工作时间 = 工作总量（一定）。 （ 2 ）比例尺一定，图上距离和实际距离。 成正比例， = 比例尺（一定）。 （ 3 ）分数值的大小一定，它的分子和分母。 成正比例， = 分数值（一定）。 （ 4 ）正方体的棱长和体积成正比例。 不成正比例， = 棱长 × 棱长（不一定）。 【 起跑线 】 1. 填一填。 （ 1 ）两种（ ）的量，一种量变化，另一种量也随着变化，当 这两种量的（ ）一定时，这两个量就成（ ）关系，这 两个量是（ ）。如果用 x 和 y 表示两种相关联的量，用 k 表示它们的比值，正比例关系可以用式子（ ）来表示。 相关联 比值 正比例 成正比例的量 （ 2 ）下面是张老师打字的时间和字数统计表，根据要求填空。 ①表中（ ）和（ ）是相关联的量，（ ）随着 （ ）的变化而变化。 ②表中第 1 组这两种量相对应两个数的比值是（ ），第 4 组两种量 相对应两个数的比值是（ ）。 时间 / 分 1 2 3 4 5 总字数 / 个 80 160 240 320 400 时间 总字数 总字数 时间 80 80 ③ 用式子表示这两个量之间的关系是（ ）。 ④这两个量（ ）正比例关系。（填“成”或“不成”） 成 2. 判断下面的量是不是成正比例关系，并说明理由。 （ 1 ）除数一定，被除数和商。 = 除数（一定），成正比例。 （ 2 ）长方形的周长一定，长方形的长和宽。 长方形的长 + 宽 = 长方形的周长 ÷2 （一定），不是相比的关系，不成正比例。 （ 3 ）一个因数一定，积和另一个因数。 = 另一个因数（一定），成正比例。 【 跳跳板 】 3. 某车间加工的零件个数与所用的时间如下表 时间 / 时 1 3 5 … 总个数 / 个 90 270 450 … （ 1 ）根据表中的数据，在下图中描出时间和加工零件总个数的对应点，再把这些点按顺序连起来。 （ 2 ）表中的两个量成（ ）比例关系。 （ 3 ）根据图像判断，这个车间 2 小时能加工多少个零件？加工 360 个零件需要多少小时？ 根据图像判断，这个车间 2 小时能加工 180 个零件，加工 360 个零件需要 4 小时。 正 【 小升初 】 4. 下图是甲、乙两车的行程情况，看图回答问题。 （ 1 ）甲 10 分钟行（ ）千米。乙 10 分钟行（ ）千米。 （ 2 ）甲车所行路程与时间成（ ）比例关系，乙车所行路程与时间成（ ）比例关系。 （ 3 ）从图上看，甲车和乙车相比，（ ）车跑得快。 12 8 正 正 甲