高考数学专题复习练习第二章 函数、 导数及其应用 质量检测
第二章 函数、导数及其应用
(时间120分钟,满分150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一 项是符合题目要求的)
1.化简[(-2)6] -(-1)0的结果为 ( )
A.-9 B.7 C.-10 D.9
解析:[(-2)6] -(-1)0=(26) -1=8-1=7.
答案:B
2.设 ( )
A. B. C.- D.
解析:f(f())=f(-)=.
答案:B
3.下列函数中,同时具有性质:(1)图象过点(0,1);(2)在区间(0,+∞)上是减函数;(3)是偶函数.这样的函数是 ( )
A.y=x3+1 B.y=log2(|x|+2) C.y=()|x| D.y=2|x|
解析:显然四个函数都满足性质(1),而满足性质(2)的只有C.
答案:C
4.下列是关于函数y=f(x),x∈[a,b]的几个命题:
①若x0∈[a,b]且满足f(x0)=0,则(x0,0)是f(x)的一个零点;
②若x0是f(x)在[a,b]上的零点,则可用二分法求x0的近似值;
③函数f(x)的零点是方程f(x)=0的根,但f(x)=0的根不一定是函数f(x)的零点;
④用二分法求方程的根时,得到的都是近似值.
那么以上叙述中,正确的个数为 ( )
A.0 B.1 C.3 D.4
解析:因为①中x0∈[a,b]且满足f(x0)=0,则x0是f(x)的一个零点,而不是(x0,0),所以①错误;
②因为函数f(x)不一定连续,所以②错误;
③方程f(x)=0的根一定是函数f(x)的零点,所以③错误;
④用二分法求方程的根时,得到的根也可能是精确值,所以④也错误.
答案:A
5.若函数f(x)=x3+f′(1)x2-f′(2)x+3,则f(x)在点(0,f(0))处切线的倾斜角为 ( )
A. B. C. D.
解析:由题意得:f′(x)=x2+f′(1)x-f′(2),
令x=0,得f′(0)=-f′(2),
令x=1,得f′(1)=1+f′(1)-f′(2),
∴f′(2)=1,∴f′(0)=-1,
即f(x)在点(0,f(0))处切线的斜率为-1,
∴倾斜角为π.
答案:D
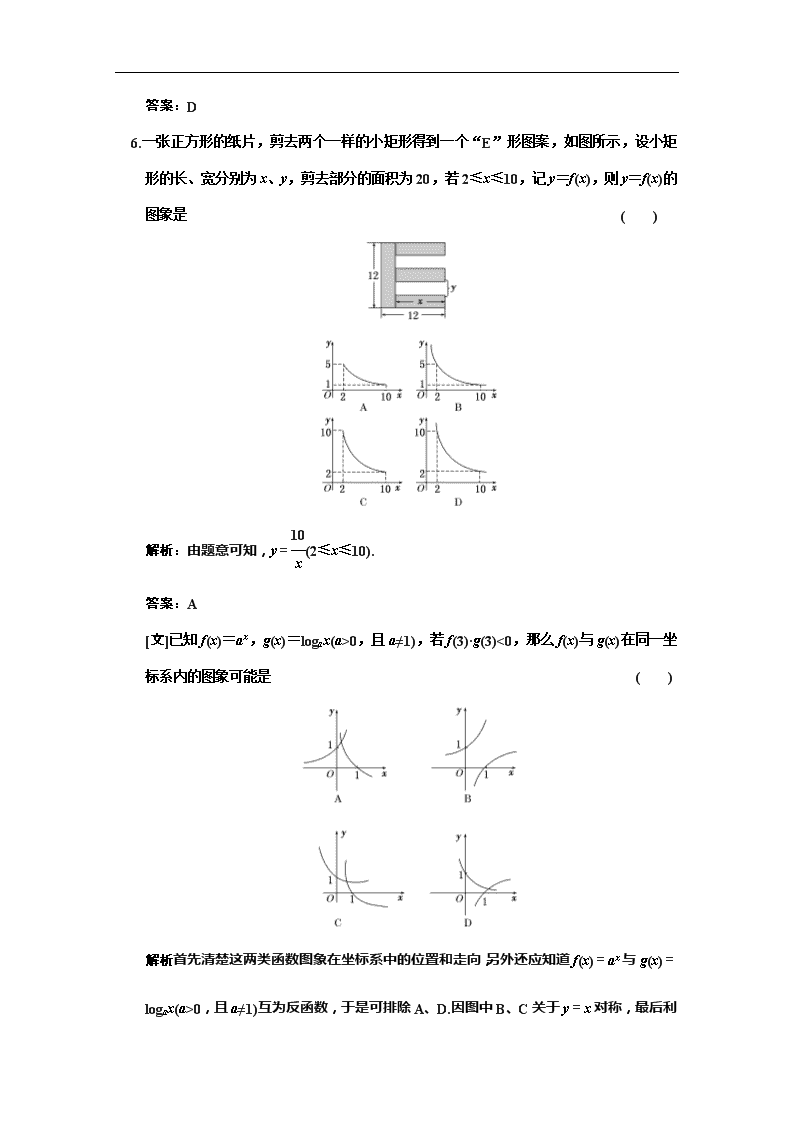
6.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”形图案,如图所示,设小矩形的长、宽分别为x、y,剪去部分的面积为20,若2≤x≤10,记y=f(x),则y=f(x)的图象是 ( )
解析:由题意可知,y=(2≤x≤10).
答案:A
[文]已知f(x)=ax,g(x)=logax(a>0,且a≠1),若f(3)·g(3)<0,那么f(x)与g(x)在同一坐标系内的图象可能是 ( )
解析:首先清楚这两类函数图象在坐标系中的位置和走向,另外还应知道f(x)=ax与g(x)=logax(a>0,且a≠1)互为反函数,于是可排除A、D.因图中B、C关于y=x对称,最后利用函数值关系式f(3)·g(3)<0,排除B,故选C .
答案:C
10.(2010·福州模拟)关于x的方程(m+3)x2-4mx+2m-1=0的两根异号,且负数根的绝对值比正数根大,那么实数m的取值范围是 ( )
A.-3
0 D.m<0或m>3
解析:∵x1x2<0,x1+x2<0,
解得-30⇒-30时,恒有f(x+Δx)>f(x),则实数a的取值范围是 .
解析:依题意,对于任意x≥2,当Δx>0时,恒有f(x+Δx)>f(x),说明函数f(x
)在[2,+∞)上是单调递增函数,所以应有,解得-4x2;②x;③|x1|>x2.
其中能使f(x1)>f(x2)恒成立的条件序号是 .
解析:函数f(x)为偶函数,f′(x)=2x+sinx,
当0<x≤时,00,函数f(x)在上为单调增函数,
由偶函数性质知函数在上为减函数.
当x>x时,得|x1|>|x2|≥0,
∴f(|x1|)>f(|x2|),由函数f(x)在上为偶函数得f(x1)>f(x2),故②成立.
∵>-,而f =f ,
∴①不成立,同理可知③不成立.故答案是②.
答案:②
15.定义在R上的函数f(x),如果存在函数g(x)=kx+b(k,b为常数),使得f(x)≥g(x)对一切实数x都成立,则称g(x)为函数f(x)的一个承托函数.现有如下命题:
①对给定的函数f(x),其承托函数可能不存在,也可能有无数个;
②g(x)=2x为函数f(x)=2x的一个承托函数;
③定义域和值域都是R的函数f(x)不存在承托函数.
下列选项正确的是 .
解析:对于①,若f(x)=sinx,则g(x)=B(B<-1),就是它的一个承托函数,且有无数个,再如y=tanx,y=lgx就没有承托函数,∴命题①正确;
对于②,∵当x=时,g()=3,f()==2=,∴f(x)0,且4-b≠0,
即(-4)2-4(4-b)>0且b≠4,
解得b>0且b≠4,
所以所求b的取值范围是(0,4)∪(4,+∞).
18.(本小题满分12分)已知函数f(x)=ax+(x≠0,常数a∈R).
(1)讨论函数f(x)的奇偶性,并说明理由;
(2)若函数f(x)在x∈[3,+∞)上为增函数,求a的取值范围.
解:(1)定义域(-∞,0)∪(0,+∞),关于原点对称.
当a=0时,f(x)=,满足对定义域上任意x,f(-x)=f(x),∴a=0时,f(x)是偶函数;
当a≠0时,f(1)=a+1,f(-1)=1-a,
若f(x)为偶函数,则a+1=1-a,a=0矛盾;
若f(x)为奇函数,
则1-a=-(a+1),1=-1矛盾,∴当a≠0时,f(x)是非奇非偶函数.
(2)任取x1>x2≥3,f(x1)-f(x2)=ax1+-ax2-
=a(x1-x2)+=(x1-x2)(a-).
∵x1-x2>0,f(x)在[3,+∞)上为增函数,
∴a>,即a>+在[3,+∞)上恒成立.
∵+<,
∴a≥.
19.(本小题满分12分)某公司生产一种产品的固定成本为0.5万元,但每生产100件需再增加 成本0.25万元,市场对此产品的年需求量为500件,年销售收入(单位:万元)为R(t)=5t-(0≤t≤5),其中t为产品售出的数量(单位:百件).
(1)把年利润表示为年产量x(百件)(x≥0)的函数f(x);
(2)当年产量为多少件时,公司可获得最大年利润?
解:(1)当0≤x≤5时,f(x)=R(x)-0.5-0.25x
=-x2+4.75x-0.5;当x>5时,
f(x)=R(5)-0.5-0.25x=12-0.25x,
故所求函数解析式为
(2)0≤x≤5时,f(x)=-(x-4.75)2+10.78125,
∴在x=4.75时,
f(x)有最大值10.78125,当x>5时,
f(x)=12-0.25x<12-0.25×5
=10.75<10.78125,
综上所述,当x=4.75时,f(x)有最大值,即当年产量为475件时,公司可获得最大年利润.
20.(本小题满分12分)定义在R上的函数f(x)满足f(x)=f(x+4),当2≤x≤6时,f(x)=
()|x-m|+n,f(4)=31.
(1)求m,n的值;
(2)比较f(log3m)与f(log3n)的大小.
解:(1)因为函数f(x)在R上满足f(x)=f(x+4),
所以4是函数f(x)的一个周期.
可得f(2)=f(6),即()+n=()+n, ①
又f(4)=31,()+n=31, ②
联立①②组成方程组解得m=4,n=30.
(2)由(1)知,函数f(x)=()+30,x∈[2,6].
因为1-2),设f(-2)=m,f(t)=n.
(1)试确定t的取值范围,使得函数f(x)在[-2,t]上为单调函数;
(2)求证:n>m;
(3)[理]若t为自然数,则当t取哪些值时,方程f(x)-m=0(m∈R)在[-2,t]上有三个不相等的实数根,并求出相应的实数m的取值范围.
解:(1)因为f′(x)=(x2-3x+3)·ex+(2x-3)·ex=x(x-1)·ex,
由f′(x)>0⇒x>1或x<0;由f′(x)<0⇒0-2时,f(-2)3=f(0),
因而f(-2)
查看更多