同安区 初中毕业班中考模拟试卷

同安区 初中毕业班中考模拟试卷

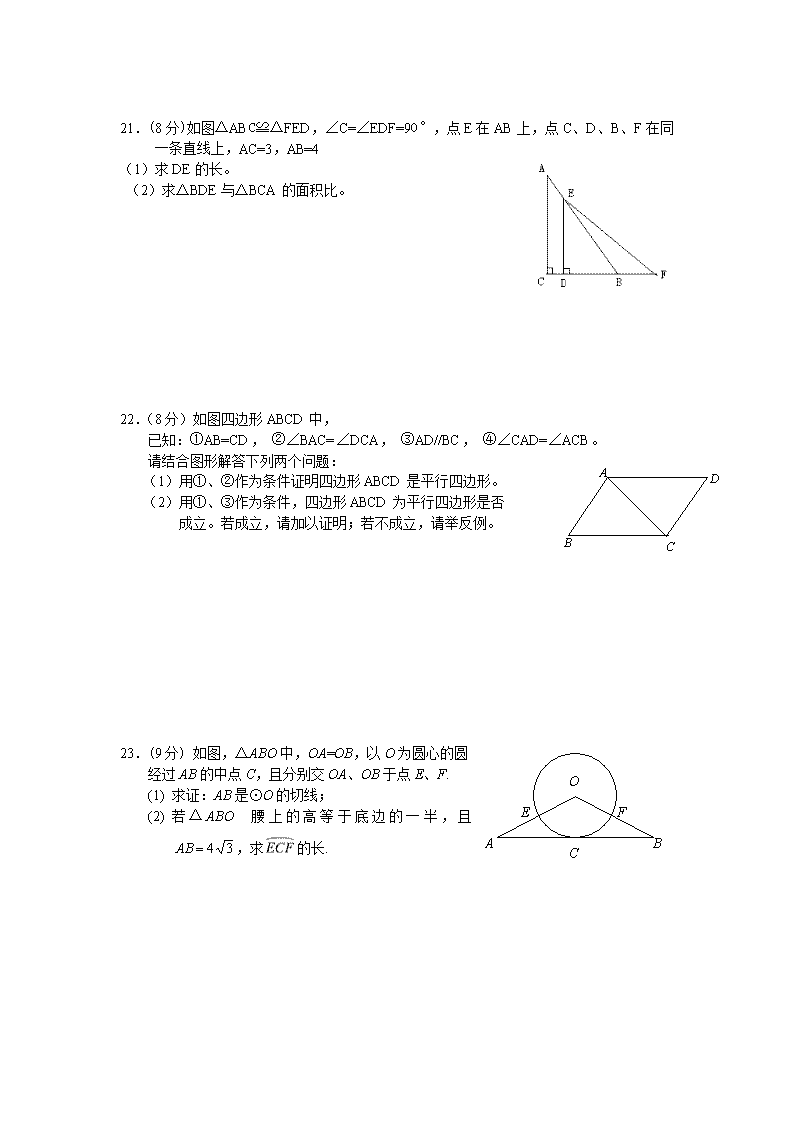
同安区09-10学年初中毕业班中考模拟试卷 1‎ ‎ 数学试题卷 班级___ 姓名___________‎ 一、选择题（本大题共7小题，每小题3分，共21分） ‎ ‎1．1．下列计算正确的是 ‎ A．－3×2＝－6 B. －1－1＝0 C. (－3)2＝6 D. 2-1＝2‎ ‎2．右图是某几何体的三种视图，则该几何体是（ 　）‎ 主视图 俯视图 左视图 A．正方体 B．圆锥体 C．圆柱体 D．球体 ‎3．下列各式计算结果正确的是（ ） ‎ A、 B、 C、 D、‎ ‎3. 如图1，在直角△ABC中，∠C＝90°,若AB＝5，AC＝4，‎ ‎ 则sin∠B＝‎ ‎ A. B. C. D. ‎4．不等式的解集是（ ）‎ A． B． C． D．‎ ‎5．下列事件，是必然事件的是 A. 掷一枚均匀的正方体骰子，骰子停止后朝上的点数是3‎ B. 掷一枚均匀的正方体骰子，骰子停止后朝上的点数不是奇数便是偶数 C. 随机从0，1，2，3…,9这十个数中选取两个数，和为20‎ D．打开电视，正在播广告 ‎ ‎6．在平行四边形中，，那么下列各式中，不能成立的是（ ）‎ A． B． C． D．‎ ‎7． 已知：a＋b＝m，ab＝－4, 化简（a－2）（b－2）的结果是 ‎ A. 6 B. 2 m－8 C. 2 m D. －2 m 二、填空题（本大题共10小题，每小题4分，共40分）‎ ‎8．的倒数是 ；‎ ‎9．已知∠A＝70º，则∠A的余角是 度．‎ ‎10．国务院总理温家宝作2009年政府工作报告时表示，今后三年各级政府拟投入医疗卫生领域资金达八千五百亿元人民币。用科学记数法表示“8500亿”的结果是： 亿。‎ ‎11．方程组的解是 ． ‎ ‎12．计算： ．‎ ‎13．一名警察在高速公路上随机观察了6辆车的车速，如下表所示：‎ 车序号 ‎ 1‎ ‎ 2‎ ‎ 3‎ ‎ 4‎ ‎ 5‎ ‎ 6‎ 车速（千米/时）‎ ‎ 85‎ ‎ 100‎ ‎ 90‎ ‎ 82‎ ‎ 70‎ ‎ 82‎ 则这6辆车车速的众数是 千米/时.‎ ‎14． 如图，内接于⊙O ，是⊙O的直径，‎ ‎，则 °．‎ ‎15．抛物线y= x2－2x+4的顶点坐标是 .‎ ‎16．已知梯形ABCD的面积是20平方厘米，高是5厘米，则此梯形 中位线的长是 厘米. ‎ ‎17．如图，把一个矩形纸片OABC放入平面直角坐标系中，使OA、‎ OC分别落在轴、轴上，连结OB，将纸片OABC沿OB折叠，‎ 使点A落在的位置上．若OB=，，求点的 坐标为_______________．‎ 三、解答题（本大题共9小题，共89分）‎ ‎18．(本题满分18分)‎ ‎（1）计算（6分）： ； ‎ ‎（2）计算（6分）： ；‎ ‎ (3) 解方程（6分）： ； ‎ ‎ ‎ ‎19．(8分)甲乙两同学参加创建全国文明城市知识竞赛，其中有4道不同的题目，题号为1，2的是选择题，题号为3，4的是判断题，甲、乙先后各随即抽取一题（抽后均不放回）‎ ‎（1）用画树状图的方法列举所有可能的抽题情况；‎ ‎（2）求甲抽到选择题的概率；‎ ‎20．(8分) “五一”假日期间，小兵和爸爸、妈妈一家三口自驾小车去某旅游景点游玩。出发时，小兵的爸爸检查了小车油箱里的存油量为30升，若该小车每行驶1千米耗油0.1升。请你解答下列问题：‎ ‎（1）写出小车油箱中的剩油量（升）与行驶路程（千米）之间的函数关系式，并求自便量的取值范围；‎ ‎ （2）为了维护车辆，小车的余油量不少于2升时，小车需重新加油，则车辆行驶多少千米时必须加油？‎ ‎21．(8分)如图△ABC≌△FED，∠C=∠EDF=90°，点E在AB上，点C、D、B、F在同一条直线上，AC=3，AB=4‎ ‎（1）求DE的长。‎ ‎ （2）求△BDE与△BCA的面积比。‎ ‎22．（8分）如图四边形ABCD中，‎ 已知：①AB=CD， ②∠BAC=∠DCA， ③AD//BC， ④∠CAD=∠ACB。‎ 请结合图形解答下列两个问题：‎ ‎（1）用①、②作为条件证明四边形ABCD是平行四边形。‎ ‎（2）用①、③作为条件，四边形ABCD为平行四边形是否 成立。若成立，请加以证明；若不成立，请举反例。‎ ‎23．(9分) 如图，△ABO中，OA=OB，以O为圆心的圆 经过AB的中点C，且分别交OA、OB于点E、F.‎ (1) 求证：AB是⊙O的切线；‎ (2) 若△ABO腰上的高等于底边的一半，且，求的长.‎ ‎24. (9分)如图，已知点在反比例函数的图象上，其中是一元二次方程的两根 ‎（1）写出与的数量关系 ；并求出的值； ‎ ‎（2）设直线AB与轴交于点，⊥轴于D点，E 点与C点关于直线AD对称，连接EB交AD于P点，求 AP的长度。‎ ‎25．(9分)已知四边形ABCD是正方形，M、N分别是边BC、CD上的动点，正方形ABCD的边长为4cm。‎ ‎（1）如图①， O是正方形ABCD对角线的交点，若OM⊥ON，求四边形MONC的面积；‎ ‎（2）如图②，若∠MAN=45°，求△MCN的周长；‎ ‎26. (11分)已知：抛物线（）与轴交于点C，点C关于抛物线对称轴的对称点为点C1．‎ ‎（1）求抛物线的对称轴及点C、C1的坐标（可用含m的代数式表示）；‎ ‎（2）如果点Q在抛物线的对称轴上，点P在抛物线上，以点C、C1、P、Q为顶点的四边形是平行四边形，求所有平行四边形的周长．‎