数学冀教版七年级上册课件1-8 有理数的乘法 第1课时

数学冀教版七年级上册课件1-8 有理数的乘法 第1课时

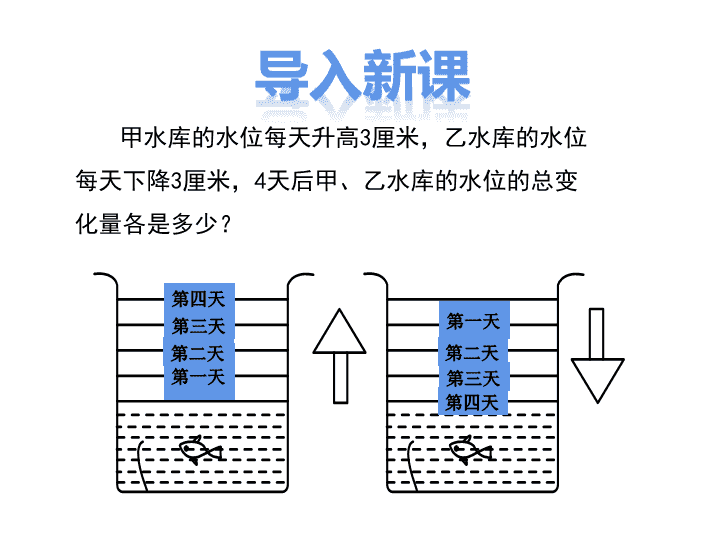
1.8 有理数的乘法 导入新课 讲授新课 当堂练习 课堂小结 第1课时 有理数的乘法法则 1.理解有理数的乘法法则，能利用有理数的乘法法则进 行简单的有理数乘法运算；(重点、难点） 2.掌握倒数的概念,会求一个数的倒数；（重点） 3.会用有理数的乘法解决实际问题.（重点） 甲水库的水位每天升高3厘米，乙水库的水位 每天下降3厘米，4天后甲、乙水库的水位的总变 化量各是多少？ 第一天 第二天 第三天 第四天 第一天 第二天 第三天 第四天 如图,一只蜗牛沿直线 l爬行，它现在的位置在 l上的点Ｏ． l Ｏ 1.如果一只蜗牛向右爬行2cm记为+2cm，那么向左爬行 2cm应该记为 . 2.如果3分钟以后记为+3分钟，那么3分钟以前应该 记为 . -2cm -3分钟 有理数的乘法运算 （１）如果蜗牛一直以每分２cm的速度向右爬行，３分 后它在什么位置？ （２）如果蜗牛一直以每分２cm的速度向左爬行，３分 后它在什么位置？ （３）如果蜗牛一直以每分２cm的速度向右爬行，３分 前它在什么位置？ （４）如果蜗牛一直以每分２cm的速度向左爬行，３分 前它在什么位置？ （5）原地不动或运动了零次，结果是什么？ 规定：向左为负，向右为正． 　　 向前为负，向后为正． 为了区分方向与时间： 思考 探究1 2 0 2 64 l 结果：3分钟后在l上点Ｏ 边 cm处 表示： . 右 6 （+2）×（+3）= 6 （1） （1）如果蜗牛一直以每分钟２ cm的速度向右爬行，３分 钟后它在什么位置？ （２）如果蜗牛一直以每分钟２ cm的速度向左爬行，３分 钟后它在什么位置？ 探究2 -6 -4 0-2 2 l 结果：3分钟后在l上点Ｏ 边 cm处左 6 表示： . （-2）×（+3）＝ （2）－６ （３）如果蜗牛一直以每分钟２ cm的速度向右爬行，３分 钟前它在什么位置？ 探究3 2 -6 -4 0-2 2 l 结果：3分钟前在l上点Ｏ 边 cm处 表示： . （+2）×（-3）＝ －６ 左 6 （３） （４）如果蜗牛一直以每分钟２ cm的速度向左爬行，３分 钟前它在什么位置？ 探究4 2 0 2 64-2 l 结果：3钟分前在l上点Ｏ 边 cm处右 6 表示： . （-2）×（-3）＝　　　　　　　　（4）＋６ 答：结果都是仍在原处，即结果都是 ， 若用式子表达： 　 探究5 （5）原地不动或运动了零次，结果是什么？ 0×3=0；0×(－3)=0； 2×0=0；(－2)×0=0． 零 Ｏ （＋２）×（＋３）＝＋６　 （－２）×（－３）＝＋６ （－２）×（＋３）＝－６　 （＋２）×（－３）＝－６ 同号得正 异号得负 绝对值相乘 0×3=0；0×(－3)=0； 2×0=0；(－2)×0=0． 任何数同0相乘，仍得0. 有理数乘法法 则 两数相乘，同号得正，异号得负，并把绝对值相乘. 任何数同0相乘，仍得0. 讨论: (1)若a＜0,b＞0,则ab_____0 ; (2)若a＜0,b＜0,则ab_____0 ; (3)若ab＞0,则a、b应满足什么条件？ (4)若ab＜0,则a、b应满足什么条件？ ＜ ＞ a、b同号 a、b异号 例1 计算： 1 ( 3) 7 （） ； 0.1 ( 100) （2） ； 16 6  （3）（- ）（ ）； 1 1( ). 2 3  （4）（- ） 解： 1 ( 3) 7 （） (3 7) 21.      0.1 ( 100) （2） 0.1 100)=-( =-10. 16 6  （3）（-）（ ） 1 1( ) 2 3  （4）（- ） 16 6 =+( ） =1. 1 1) 2 3 1. 6   =+( 有理数乘法的求 解步骤: 再求绝对值的积. 计算： （1）（-5）×（-6）； （2） 3 1( ) ; 2 6   （3） 3 5( ) ( ); 5 3    （4）8×（-1.25）. 解：（1）（-5）×（-6）=+(5×6)=30. （2） 3 1 3 1 1( ) ( ) . 2 6 2 6 4        （3） 3 5 3 5( ) ( ) ( ) 1 . 5 3 5 3        （4） 8×（-1.25)=-(8×1.25)=-10. 计算： （1） ×2；　　　（2）(- )×(-2) 观察上面两题有何特点? 结论: 如果两个数的乘积是1，那么我们称这两个有理数 互为倒数，其中一个数称为另一个数的倒数. （2）（- ）×（-2）= 1 1 2 解：（1） ×2 = 1 1 2 1 2 1 2 倒数 说出下列各数的倒数： １，－１， ，－ ，５，－５，0.75，－1 3 1 3 1，－１， 3， —3， 1 , 5 1- , 5 3 12 4 , 3 3- 7 （1）求一个数的倒数，不能改变它的性质符号，即一 个正数的倒数是正数，一个负数的倒数是负数； （2）求小数或带分数时的倒数时，先将小数或带分数 化为分数或者假分数，再颠倒其分子和分母的位置. 例2 通常情况下，海拔高度每增加1km，气温就降低大约 6℃（气温降低为负）.某校七年级科技兴趣小组在海拔高 度为1000m的山腰上，测得气温是12℃.请你推算此山海拔g 高度为3500m处的气温大约是多少. 解：1000m=1km,3500m=3.5km. 12+(-6)×(3.5-1) =12+(-15) =-3(℃). 答：气温大约是零下3℃. 有理数的乘法的应用 被乘数 乘数 积的符号 积的绝对值 结果 －5 7 15 6 －30 －6 4 －25 1.填空题 － 35 －35 + 90 90 + 180 180 － 100 －100 2.（1）若 互为相反数，且 ，则 ________， ________； ,a b a b a b  2 2b a  －1 0 （2）-1的倒数是______, _______的倒数是 .3 11－1 3 4  解： 11 2  （） 2 （-4）=-(2.5 4)=-10 ; 7 5 7 5 1) ; 10 21 10 21 6   （2）（- （- ）= 5 54 5 2; 27 5 27   （3）(-10.8)（- ）= 13 ) 0 0. 2  （4） （- 3.计算 11 2 （） 2 （-4）； 7 5) 10 21 （2） （- （- ）； 5 27 （3） (-10.8)（- ）； 13 ) 0. 2 （4）（- 4.气象观测统计资料表明，在一般情况下，高度每上 升1km,气温下降6℃.已知甲地现在地面气温为21℃， 求甲地上空9km处的气温大约是多少？ 解：（-6）×9=-54（℃）； 21+（-54）=-33（℃）. 答：甲地上空9km处的气温大约为-33℃. 1.有理数乘法法则: 两数相乘，同号得正，异号得负，并把绝对值相乘. 2.有理数乘法的求解步骤： 有理数相乘，先确定积的符号，再求绝对值的积. 任何数同0相乘，仍得0. 3.倒数: 如果两个有理数的乘积是1，那么我们称这两个有理 数互为倒数，其中一个数是另一个数的倒数.