人教版七年级上数学教学课件：角（3）

人教版七年级上数学教学课件：角（3）

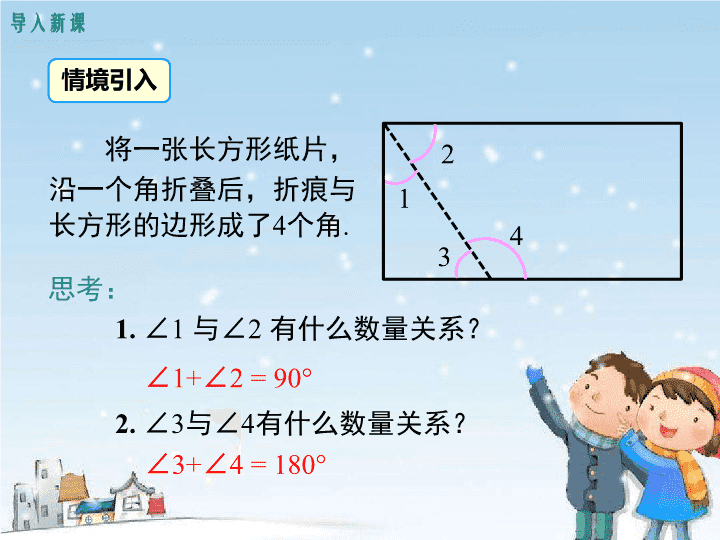
4.3.3 余角和补角 第四章 图形初步认识 导入新课 讲授新课 当堂练习 课堂小结 4.3 角 学习目标 1. 了解余角、补角 的概念，掌握余角和补角的性质， 并能利用余角、补角的知识解决相关问题 . ( 重点、 难点 ) 2. 了解方位角的概念，并能用方位角知识解决一些 简单的实际问题 . ( 难点 ) 导入新课 情境引入 将一张长方形纸片，沿一个角折叠后，折痕与长方形的边形成了 4 个角 . 1 2 3 4 思考： 1. ∠1 与 ∠2 有什么数量关系？ ∠1+∠2 = 90 ° 2. ∠3 与 ∠4 有什么数量关系？ ∠3+∠4 = 180 ° 讲授新课 余角和补角的概念 一 1 如果两个角的和等于 90 ° ( 直角 ) ，就说这两个角互为 余角 ( 简称为两个角互余 ). 如图，可以说 ∠1 是 ∠2 的余角，或 ∠2 是 ∠1 的余角，或 ∠1 和 ∠2 互余 . 2 图中给出的各角，哪些互为余角？ 15 o 24 o 66 o 75 o 46.2 o 43.8 o 如果两个角的和等于 180 ° ( 平角 ) ，就说这两个角互为 补角 ( 简称为两个角互补 ). 如图，可以说 ∠3 是 ∠4 的补角，或 ∠4 是 ∠3 的补角，或 ∠3 和 ∠4 互补 . 4 3 图中给出的各角，哪些互为补角？ 10 o 30 o 60 o 80 o 100 o 120 o 150 o 170 o 例 1 若一个角的补角等于它的余角的 4 倍，求这个角的度数 . 解：设这个角为 x ° ，则它的补角是 ( 180 － x ) °， 余角是 ( 90 － x ) ° . 根据题意，得 180 － x = 4 ( 90 － x ) . 解得 x = 60. 答：这个角的度数是 60 °. 典例精析 练一练 已知 ∠ A 与 ∠ B 互余，且 ∠ A 的度数比 ∠ B 度数的 3 倍还多 30° ，求 ∠ B 的度数 . 解：设 ∠B 的度数为 x °，则 ∠ A 的度数为 (3 x +30) ° . 根据题意得： x + ( 3 x +30 ) = 90. 解得 x =15. 故 ∠ B 的度数为 15 ° . 例 2 如图，已知O为AD上一点，∠AOC与∠AOB互补，OM，ON分别为∠AOC，∠AOB的平分线，若∠MON=40°，试求∠AOC与∠AOB的度数． O D A B C N M 解：设∠AOB= x ， 因为∠AOC与∠AOB互补， 则∠AOC=180° - x ． 因为OM，ON分别为∠AOC， ∠AOB的平分线， 所以∠AO M= ，∠AO M= . O D A B C N M 所以 解得 x =50 °，则 180 ° - x =130 ° . 即∠AOB =50 °， ∠AOC =130 ° . ∠α ∠α 的余角 ∠α 的补角 5 ° 32 ° 45 ° 77 ° 62 ° 23 ′ x ° (0 ＜ x ＜ 90) 27°37′ 117°37′ 85° 175° 58° 148° 45° 135° 103° 13° 观察与思考 (90 － x )° (180 － x )° 观察可得结论： 锐角的补角比它的余角大 _____. 90° ∠ 1 与∠ 2 ，∠ 3 都互为补角， ∠ 2 与∠ 3 的大小有什么关系？ 余角和补角的性质 二 思考： 1 2 同角 ( 等角 ) 的补角相等 . 结论： 3 ∠ 2=180 °－∠ 1 ∠ 3=180 °－∠ 1 同角 ( 等角 ) 的余角相等 . 类似地，可以得到： = 例 3 如图，点 A ， O ， B 在同一直线上，射线 OD 和射线 OE 分别平分∠ AOC 和∠ BOC ，图中哪些角互为余角？ 解：因为点 A ， O ， B 在同一直线 上，所以 ∠ AOC 和 ∠ BOC 互为补角 . O A B C D E 又因为射线 OD 和射线 OE 分别平分∠ AOC 和∠ BOC ，所以∠ COD + ∠ COE = ∠ AOC + ∠ BOC = ( ∠ AOC + ∠ BOC ) = 90 ° . O A B C D E 所以∠ COD 和∠ COE 互为余角， 同理∠ AOD 和∠ BOE ，∠ AOD 和∠ COE ，∠ COD 和∠ BOE 也互为余角 . 如图，O为直线AB上一点，OD平分∠AOC，∠DOE=90°． （1）∠AOD的余角是 _______________ ，∠COD的余角是 _________________; （2 ）OE是∠BOC的平分线吗？请说明理由． 变式训练 ∠COE、∠BOE O A B C D E ∠COE、∠BOE 解：OE平分∠BOC，理由如下：∵∠DOE=90°，∴∠AOD+∠BOE=90°， ∴∠COD+∠DOE=90°， ∴∠AOD+∠BOE=∠COD+∠DOE， ∵OD平分∠AOC∴∠AOD=∠COD， ∴∠COE=∠BOE，∴OE平分∠BOC． 如图 , 已知 ∠ AOB =90° ， ∠ AOC = ∠ BOD ，则与 ∠ AOC 互余的角有 _________ _____ ____. ∠ BOC 和 ∠ AOD 练一练 O A B C D 方位角 三 互动探究 观看下列视频，议一议其中蕴含的数学知识 . 东 西 北 南 O 正东： 正南： 正西： 正北： 西北方向： 西南方向： 东北方向： 东南方向： 射线 OA A B C D 45° E G F H 45° 八大方位 45° 45° 射线 O B 射线 O C 射线 O D 射线 O E 射线 O F 射线 O H 射线 O G 45 ° 如图，说出下列方位 ( 1 ) 射线 OA 表示的方向 为 . ( 2 ) 射线 OB 表示的方向 为 ___ _ . ( 3 ) 射线 OC 表示的方向 为 . ( 4 ) 射线 OD 表示的方向 为 . 北 东 西 南 C A B D 北偏东 40 ° 北偏西 65 ° 南偏西 45 ° ( 西南 ) 南偏东 20 ° 40 ° 65 ° 70 ° O 20 ° 例 4 如图，货轮 O 在航行过程中，发现灯塔 A 在它南偏东 60° 的方向上 . 同时，在它北偏东 40° ，南偏西 10° ，西北 ( 即北偏西 45°) 方向上又分别发现了客 轮 B ，货轮 C 和海岛 D . 仿照表示灯塔方位的 方法画出表示客轮 B ， 货轮 C 和海岛 D 方向的 射线 . 东 南 西 北 60° ● B 40° 10° 45° C ● ● A ● D O ● 费俊龙、聂海胜乘坐 “ 神舟”六号遨游太空时，我国当时派出远望一号 ~ 四号船队，跟踪检测 . 其中远望一、二号停在太平洋洋面上，某一时刻，分别测得神舟六号在北偏东 60° 和北偏东 30° 的方向，你能在下图中画出当时神舟六号所处的位置吗？ ● ● 远望一号 远望二号 练一练 ● ● 远望一号 远望二号 60° 30° ● 当堂练习 1. 一个角的余角是它的2倍，这个角的度数是（　） A．30° B．45° C．60° D．75° A 2. 下列说法正确的是（　　） A．一个角的补角一定大于它本身 B．一个角的余角一定小于它本身 C．一个钝角减去一个锐角的差一定是一个锐角 D．一个角的余角一定小于其补角 D 3. 已知∠A与∠B互余，∠B与∠C互补，若∠A=60°，则∠C的度数是 _______. 150 ° 4. ∠1 与 ∠2 互余， ∠1 = (6 x + 8) °， ∠2 = (4 x － 8) °， 则 ∠1= ， ∠2= . 62 ° 28 ° 5. 如图，已知 ∠ ACB= ∠CDB=90 ° . ( 1 ) 图中有哪几对互余的角？ ( 2 ) 图中哪几对角是相等的角 ( 直角除外 ) ？为什么？ 答案： ∠ A +∠ B =90° ∠ A +∠2=90° ∠1+∠ B =90° ∠1+∠2=90° 答案： ∠ B =∠2 ∠ A =∠1 ( 同角的余角相等 ) ( 同角的余角相等 ) A C D 1 2 B 60 ° 30 ° 6. 垃圾打捞船 A 和 B 都停驻在湖边观测湖面，从 A 船发现它的北偏东 60 °方向有白色漂浮物， 同时，从 B 船也发现该白色漂浮物在它的北偏 西 30 °方向 . ( 1 ) 试在图中确定白色漂浮物 C 的位置； A B 北 北 C 60 ° 北 A. 南偏东 30° B. 南偏西 30° C. 南偏东 60° D. 南偏西 60° ( 2 ) 点 C 在点 A 的北偏东 60 °的方向上，那么点 A 在点 C 的 ______ 方向上 . 60 ° 30 ° A B 北 北 C D 同角或等角的 补角相等 课堂小结 同角或等角的 余角相等 互余 互补 两角间的数量关系 对应图形 性质 方位角 物体运动的方向与正北、正南方向之间的夹角称为方位角，一般以正北、正南为基准，用向东或向西旋转的角度表示方向 定义 书写 通常要先写北或南，再写偏东或偏西