北师大版数学九年级上册同步练习课件-第1章 特殊平行四边形-第1章 3 第2课时正方形的判定

北师大版数学九年级上册同步练习课件-第1章 特殊平行四边形-第1章 3 第2课时正方形的判定

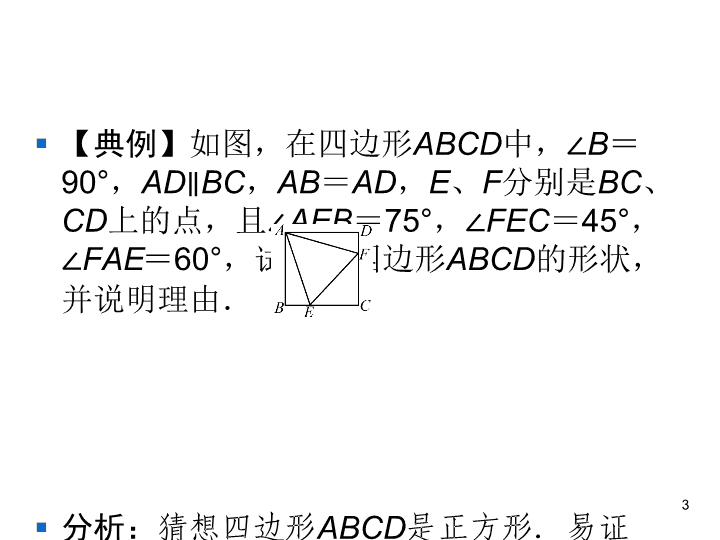
第一章　特殊平行四边形 3　正方形的性质与判定 第二课时　正方形的判定 § 知识点　正方形的判定定理 § (1)有一组邻边相等的矩形是正方形． § (2)对角线互相垂直的矩形是正方形． § (3)有一个角是直角的菱形是正方形． § (4)对角线相等的菱形是正方形． § 注意：判定一个正方形的一般顺序：先证明 它是平行四边形→再证明它是菱形(或矩 形)→最后证明它是正方形． 2 § 【典例】如图，在四边形ABCD中，∠B＝ 90°，AD∥BC，AB＝AD，E、F分别是BC、 CD上的点，且∠AEB＝75°，∠FEC＝ 45°，∠FAE＝60°，试判断四边形ABCD 的形状，并说明理由． § 分析：猜想四边形ABCD是正方形．易证 △AEF是等边三角形，进而证得 △ABE≌△ADF，得到∠D＝∠B＝90°，进 一步证得四边形ABCD是平行四边形，在此 基础上即可证得结论． 3 § 解答：四边形ABCD是正方形．理由： § ∵∠AEB＝75°，∠FEC＝45°， § ∴∠AEF＝60°. § 又∵∠FAE＝60°， § ∴△AEF是等边三角形， § ∴AE＝AF. § ∵AD∥BC，∠B＝90°， § ∴∠DAB＝90°. § ∵∠BAE＝180°－∠B－∠AEB＝15°， § ∴∠DAF＝∠DAB－∠BAE－∠FAE＝15°， § ∴∠BAE＝∠DAF. 4 5 § 1．下列说法中正确的是(　　) § A．对角线相等且有一个角是直角的平行四边形是正方形 § B．对角线互相垂直且一组邻边相等的平行四边形是正方形 § C．四个角都相等的菱形是正方形 § D．对角线互相垂直平分且有一组邻边相等的四边形是正方形 § 2．在四边形ABCD中，∠A＝∠B＝∠C＝90°，如果再添加一个条件， 即可推出该四边形是正方形，这个条件可以是(　　) § A．BC＝CD B．AB＝CD § C．∠D＝90° D．AD＝BC 6 C　 A 　 § 3．在四边形ABCD中，对角线AC、BD相交于点O，若AO＝CO＝BO＝ DO，AC⊥BD，则四边形ABCD的形状为(　　) § A．平行四边形 B．菱形 § C．矩形 D．正方形 § 4．【甘肃兰州中考】在平行四边形ABCD中，对角线AC与BD相交于点 O，要使四边形ABCD是正方形，还需添加一组条件．下面给出了四组 条件：①AB⊥AD，且AB＝AD；②AB＝BD，且AB⊥BD；③OB＝OC， 且OB⊥OC；④AB＝AD，且AC＝BD.其中正确的序号是___________. 7 D 　 ①③④　 § 5．如图，BD是△ABC的角平分线，DE∥BC，交AB于点E，DF∥AB， 交BC于点F，当△ABC满足条件____________________________时， 四边形BEDF是正方形． 8 ∠ABC＝90°(答案不唯一)　 § 6．如图，在矩形ABCD中，M、N分别是边AD、BC的中点，E、F分别 是边BM、CM的中点，当AB∶ AD＝___________时，四边形MENF是 正方形． 9 1∶ 2　 § 7．如图，在Rt△ABC中，∠C＝90°，∠BAC、∠ABC的平 分线相交于点D，DE⊥BC，DF⊥AC，垂足分别为E、F.求 证：四边形CEDF是正方形． § 证明：如题图，过点D作DN⊥AB于点N.∵∠C＝90°， DE⊥BC，DF⊥AC，∴四边形CEDF是矩形．∵∠BAC、 ∠ABC的平分线相交于点D，DE⊥BC，DF⊥AC，DN⊥AB， ∴DF＝DN，DE＝DN，∴FD＝ED，∴四边形CEDF是正方 形． 10