- 2021-02-26 发布 |
- 37.5 KB |
- 30页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
六年级下册数学课件 第6课时 圆锥的体积 苏教版(共30张PPT)
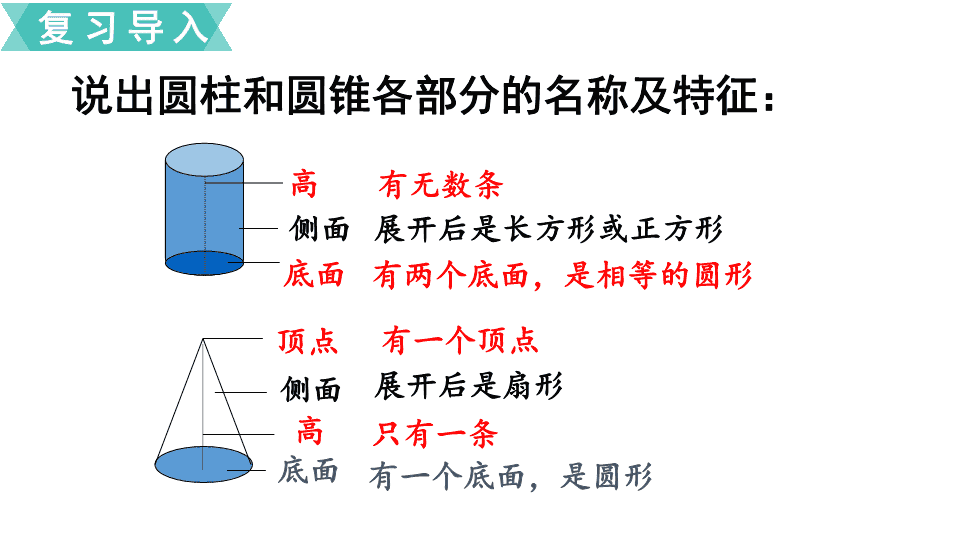
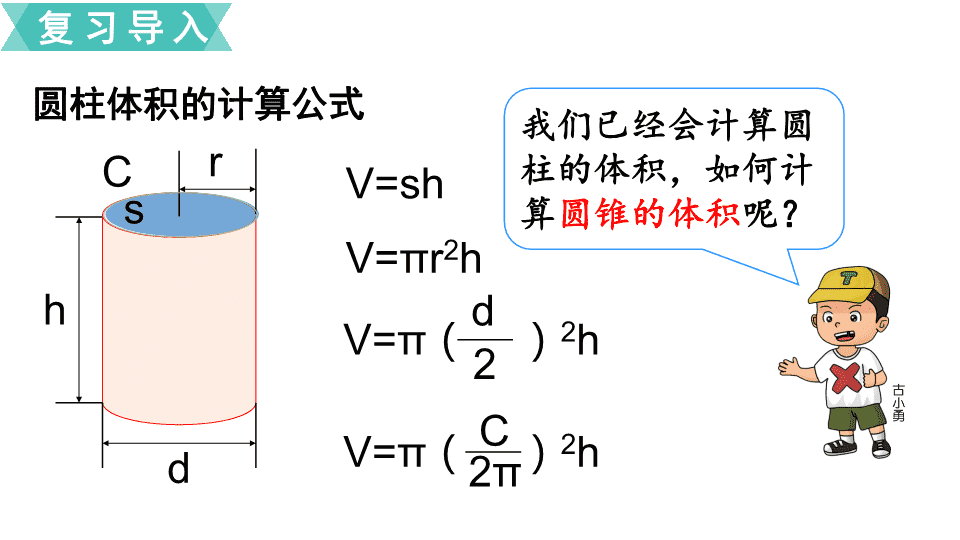
圆锥的体积 圆柱和圆锥 二 义务教育苏教版六年级下册 说出圆柱和圆锥各部分的名称及特征: 高 有无数条 侧面 展开后是长方形或正方形 底面 有两个底面,是相等的圆形 顶点 有一个顶点 侧面 展开后是扇形 高 只有一条 有一个底面,是圆形 底面 复习导入 圆柱体积的计算公式 V=sh h d s V=πr 2 h r V=π ( ) 2 h 2 d V=π ( ) 2 h 2π C C 我们已经会计算圆柱的体积,如何计算 圆锥的体积 呢? 复习导入 下面的圆柱和圆锥底面积相等,高也相等。你能估计出这个圆锥的体积是圆柱的几分之几吗? 探究新知 知识点 1 :圆锥的体积计算公式 探究新知 我们可以通过实验来检验自己的估算。 我们先准备等底等高的圆柱形容器和圆锥形容器各一个。 等 高 等底 探究新知 用倒沙子的方法试一试。 探究新知 探究新知 探究新知 探究新知 探究新知 探究新知 探究新知 探究新知 探究新知 探究新知 圆锥的体积正好是与它等底等高的圆柱体积的几分之几?你的估计对吗?与同学交流。 探究新知 实验器材 实验过程 ①在空圆柱里装满沙倒入空圆锥里,( )次,正好倒完。 ① 在空圆锥里装满沙倒入空圆柱里, ( )次正好装满。 结 论 ②圆柱的体积是和它等底等高的圆锥体积的( )倍 圆锥体积 计算公式 V= ②圆锥的体积是和它等底等高的圆柱体积的 实 验 报 告 表 3 3 3 3 1 3 1 S h 一桶沙、等底等高 的圆柱和圆锥各一个 探究新知 V = sh 1 3 V 圆柱 = sh 圆锥的体积 V 等于和它 等底等高 的圆柱体积的 三分之一 探究新知 底面积和高 底面半径和高 底面直径和高 底面周长和高 圆锥体积 计算圆锥的体积所必须的条件可以是: V = sh 1 3 探究新知 探究新知 比较等底等高的圆柱和圆锥, 先观察猜想,再验证。 从已经学过的圆柱 体积公式想起。 回顾圆锥体积公式的探索过 程,你有什么体会? 实验也是解决问 题的重要方法。 试一试 一个圆锥形零件,底面积是 170 平方厘米,高是 12 厘米。这个零件的体积是多少立方厘米? 170×12× = 680 (立方厘米) 3 1 答:这个零件的体积是 680 立方厘米。 知识点 2 :圆锥体积计算公式的应用 练一练 1. 一个圆柱和一个圆锥底面积相等,高也相等。圆柱的体积是 9.42 立方厘米,圆锥的体积是多少立方厘米? 9.42× = 3.14 (立方厘米) 3 1 答:圆锥的体积是 3.14 立方厘米。 如果圆锥的体积是 9.42 立方厘米,圆柱的体积是多少? 9.42×3 = 28.26 (立方厘米) 答:圆柱的体积是 28.26 立方厘米。 2. 计算圆锥的体积。 (单位: cm ) 3.14×2²×6× = 25.12 ( cm³ ) 3 1 3.14× ( 3÷2 ) ²×3× = 7.065 ( cm³ ) 3 1 练一练 课堂检测 1. 计算下面各圆锥的体积。 ( 1 )底面积是 15 平方厘米,高是 8 厘米。 ( 2 )底面半径是 3 分米,高是 5 分米。 ( 3 )底面直径是 0.4 米,高是 0.6 米。 ×15×8 = 40 (立方厘米) ×3.14×3²×5 = 47.1 (立方分米) ×3.14× ( 0.4÷2 ) ²×0.6 = 0.02512 (立方米) (教材 22 页第 1 题) 2. 有两个玻璃容器 (如下图) 。在圆锥形容器里注满水,倒入空的圆柱形容器,圆柱形容器里水深多少厘米? 3.14× ( 10÷2 ) ²× h = ×3.14× ( 10÷2 ) ²×12 h = 4 解:设圆柱形容器 里水深 h cm 。 课堂检测 (教材 22 页第 2 题) 课堂检测 (教材 22 页第 3 题) 3. 一个近似于圆锥形的野营帐篷,底面半径是 3 米,高是 2.4 米。 ( 1 )帐篷的占地面积是多少? ( 2 )帐篷里的空间有多大? 3.14×3² = 28.26 (平方米) ×3.14×3²×2.4 = 22.608 (立方米) 4. 一堆煤成圆锥形,高 2m ,底面周长为 18.84m 。这堆煤的体积大约是多少?已知每立方米的煤约重 1.4t ,这堆煤大约重多少吨?(得数保留整数。) V = π ( ) 2 h 2π C 这堆煤的体积×每立方米煤的质量 巩固练习 ×3.14× ( 18.84÷3.14÷2 ) 2 ×2 ≈ 19 ( m 3 ) 1 3 答:这堆煤的体积大约是 19m 3 。这堆煤大约重 27 吨。 19×1.4 ≈ 27 (吨) 巩固练习 课堂小结 通过这节课的学习活动,你有什么收获? 1. 圆锥的体积是与它等底等高的圆柱的体积 的 。 2. 圆锥的体积=底面积 × 高 × 。 3. 已知圆锥的底面积和高,可以利用公式 V = S h 直接代入数据计算出圆锥的体积。 3 1 3 1 3 1查看更多