中考数学一轮复习知识点+题型专题讲义07 不等式(组)(学生版)
专题 07 不等式(组)
考点总结
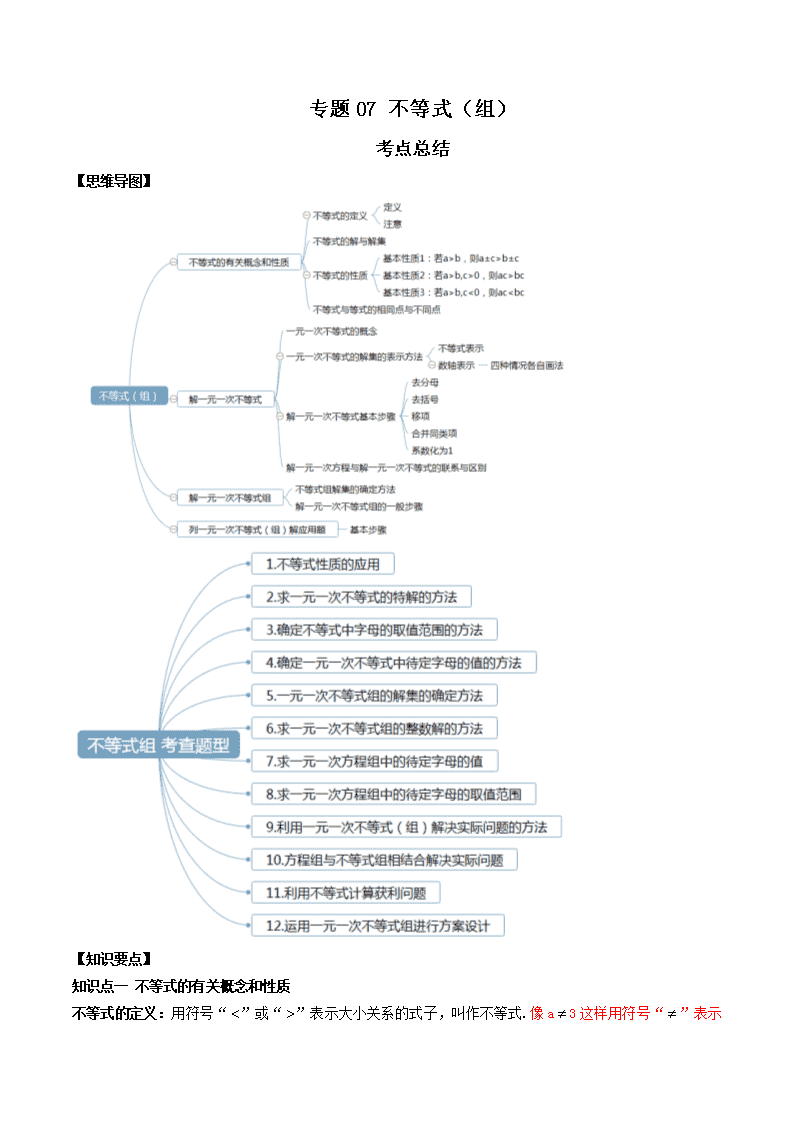
【思维导图】
【知识要点】
知识点一 不等式的有关概念和性质
不等式的定义:用符号“ ”或“ ”表示大小关系的式子,叫作不等式.像 a 3 这样用符号“ ”表示
不等关系的式子也是不等式。
【注意】
1.方程与不等式的区别:方程表示的是相等关系,不旁式表示的是不等关系。
2.常用的不等号有“ , , , , ”五种.“ ”“ ”不仅表示左右两边的不等关系,还明确表示左右两边
的大小;“ ”“ ”也表示不等关系,前者表示“不小于”(大于或等于),后者表示“不大于”(小于或等
于);“ ”表示左右两边不相等。
3.在不等式 a>b 或 a
b,则 a+c>b+c,a-c>b-c。
基本性质 2:不等式两边同时乘以(或除以)同一个大于 0 的整式,不等号方向不变,即
若 a>b,c>0,则 ac>bc(或
�
� �
�
�
)
基本性质 3:不等式两边同时乘以(或除以)同一个小于 0 的整式,不等号方向改变,即
若 a>b,c<0,则 acb,则 bb>c,则 a>c。
基本性质 6:如果 a b ,c d ,那么 a c b d .
【注意】
1、根据不等式的性质,可以将一个不等式变形,尤其要注意性质 2 和性质 3 的区别,当不等式两边乘(或
除以)同一个负数时,不等号的方向要改变。
2、不等号方向发生改变就是指原来的不等号方向变成其相反方向。
不等式性质与等式性质的相同和不同点:
相同点:都可以在两边加上或减去同一个式子
不同点:
1、 对于等式两边,乘(或除)以同一个正数(或负数),结果依然成立
2、 对于不等式两边,乘(或除)以同一个正数,不等号方向不变;乘(或除)以同一个负数,不等号方向
发生改变;
解不等式的概念:求不等式的解集的过程叫作解不等式。
【典型例题】
1.(2019·阜宁县容山中学初一期末)下列不等式中,是一元一次不等式的是( )
A.x y B. 2 2 0a b C. 1 1x
D. 3
4 x 4 03
2.(2019·重庆市南坪中学校初二期中)下列各式中,是一元一次不等式的有( )
① 5x ,② ( 5) 5x x ,③ 1 5x
,④ 2 5x y y ,⑤ 2 5a ,⑥
3
yx
A.2 个 B.3 个 C.4 个 D.5 个
【考查题型】
考查题型一 不等式性质的应用
1.(2019·四川中考真题)若 m n> ,下列不等式不一定成立的是( )
A. 3 3m n > B. 3 3m n﹣ <﹣ C.
3 3
m n D. 2 2m n>
2.(2019·浙江中考真题)已知四个实数 a,b,c,d,若 a>b,c>d,则( )
A.a+c>b+d B.a-c>b-d C.ac>bd D. a b
c d
3.(2019·上海中考真题)如果 m﹥n,那么下列结论错误的是( )
A.m+2﹥n+2 B.m-2﹥n-2 C.2m﹥2n D.-2m﹥-2n
4.(2019·江苏中考真题)实数 a、b、c 满足 a>b 且 ac<bc,它们在数轴上的对应点的位置可以是( )
A. B.
C. D.
知识点二 解一元一次不等式
一元一次不等式的概念:不等式的左右两边都是整式,只含有一个未知数并且未知数的最高次数是 1,像这
样的不等式叫一元一次不等式.一元一次不等式的一般形式为: 0ax b 或 0 0ax b a 。
例如, 1 3x , 4 02
y 是一元一次不等式,而 0x y , 2 5 3xx
不是一元一次不等式。
一元一次不等式的解集的表示方法:
表示的两种形式:①用不等式表示;②用数轴表示。
下面我们讨论用数轴表示一元一次不等式解集的四种情况:
【注意】
1、 用数轴表示不等式解集时要“两定”:定边界点,定方向。
2、 若符号为“>或<”时,边界点为空心,若符号为“≥或≤”,边界点为实心。
3、 定方向时要注意“小于向左,大于向右”。
解一元一次不等式的一般步骤:
1 去分母;②去括号;③移项;④合并同类项;⑤未知数的系数化为 1
解一元一次方程和解一元一次不等式的区别:
一元一次方程 一元一次不等式
解法的依据 方程得两边加(或减)同一个数
(或式子),方程的解不变
方程的两边乘(或除以)同一个
不为零的数,方程的解不变
不等式两边加(或减)同一个数(或式
子),不等号的方向不变
不等式的两边乘(或除以)同一个正数,
不等号的方向不变
不等式的两边乘(或除以)同一个负数,
不等号的方向改变
解法的步骤 ①去分母;②去括号;③移项;
④合并同类项;⑤未知数的系数
化为 1
①去分母;②去括号;③移项;④合并
同类项;⑤未知数的系数化为 1
在步骤①和步骤⑤中,如果乘数(或除
以)是负数,不等号要改变方向
解得情况 一元一次方程只有一个解 一元一次不等式可以有无数多个解
【典型例题】
1.(2018·广东中考模拟)不等式 2x-5≥-1 的解集在数轴上表示正确的是( ).
A. B.
C. D.
2.(2019·太原市第五十三中学初二期中)用不等式表示图中的解集,其中正确的是( )
A.x≥-2 B.x≤-2 C.x<-2 D.x>-2
3.(2019·河北初一期末)已知
�� � � ͵ �
,要使
�
是负数,则
�
的取值范围是( )
A.
� �
B.
� �
C.
� �㐲
D.
㐲 � � � 【考查题型汇总】
考查题型二 求一元一次不等式的特解的方法
1.(2019·江苏中考真题)不等式 1 2x 的非负整数解有( )
A.1 个 B.2 个 C.3 个 D.4 个
2.(2019·内蒙古中考模拟)不等式 3(x﹣1)≤5﹣x 的非负整数解有( )
A.1 个 B.2 个 C.3 个 D.4 个
3.(2017·广东中考模拟)如图,直线 y x m 与 4 0y nx n n 的交点的横坐标为 2 ,则关于 x 的
不等式 4 0x m nx n 的整数解为( ).
A. 1 B. 5
C. 4 D. 3
4.(2019·内蒙古中考模拟)不等式 3 1 22
x 的最小整数解是______.
考查题型三 确定不等式中字母的取值范围的方法
1.(2019·黑龙江中考真题)已知 x=4 是不等式 ax-3a-1<0 的解,x=2 不是不等式 ax-3a-1<0 的解,则实数
a 的取值范围是____.
2.(2019·四川中考真题)关于 x 的不等式 2 1x a 只有 2 个正整数解,则 a 的取值范围为( )
A. 5 3a B. 5 3a C. 5 3a D. 5 3a
3.(2012·江苏中考模拟)已知关于 x 的不等式 x≥a-1 的解集如图所示,则 a 的值为__.
考查题型四 确定一元一次不等式中待定字母的值的方法
1.(2019·河南中考模拟)若不等式组 1
3 0
x a
bx
的解集是﹣1<x≤1,则 a=_____,b=_____.
知识点三 解一元一次不等式组
一元一次不等式组的解集:一般地,几个一元一次不等式解集的公共部分,叫做它们所组成的不等式组的
解集。
不等式组解集的确定方法:
【注意】
1、 在求不等式组的解集的过程中,通常是利用数轴来确定不等式组的解集的。
2、 利用数轴表示不等式组解集时,要把几个不等式的解集都表示出来,不能仅画公共部分。
解一元一次不等式组的一般步骤:
1. 求出不等式组中各不等式的解集
2. 将各不等式的解决在数轴上表示出来。
3. 在数轴上找出各不等式解集的公共部分,这个公共部分就是不等式组的解集。
【考查题型汇总】
考查题型五 一元一次不等式组的解集的确定方法
1.(2018·湖南中考真题)不等式组 2 0
2 4 0
x
x
的解集在数轴上表示正确的是( )
A. B.
C. D.
2.(2019·山东中考模拟)一元一次不等式组
2 0
11 03
x
x
的解集在数轴上表示出来,正确的是( )
A. B. C. D.
3.(2019·江苏中考模拟)下列四个不等式组中,解集在数轴上表示如图所示的是( )
A. 2
3
x
x
B. 2
3
x
x
C. 2
3
x
x
D. 2
3
x
x
4.(2019·广东中考模拟)不等式组 2 1 3
3 1 2
x
x
<
的解集在数轴上表示正确的是( )
A. B. C.
D.
考查题型六 求一元一次不等式组的整数解的方法
1.(2019·台湾中考真题)阿慧在店内购买两种蛋糕当伴手礼,如图为蛋糕的价目表.已知阿慧购买10盒蛋
糕,花费的金额不超过 2500 元.若他将蛋糕分给 75位同事,每人至少能拿到一个蛋糕,则阿慧花多少元
购买蛋糕?( )
A. 2150 B. 2250 C. 2300 D. 2450
2.(2019·四川中考真题)红星商店计划用不超过 4200 元的资金,购进甲、乙两种单价分别为 60 元、100
元的商品共 50 件,据市场行情,销售甲、乙商品各一件分别可获利 10 元、20 元,两种商品均售完.若所
获利润大于 750 元,则该店进货方案有( )
A.3 种 B.4 种 C.5 种 D.6 种
3.(2019·浙江中考模拟)如图,等腰三角形 ABC 的周长为 20cm,底边 BC 长为 y(cm),腰 AB 长为 x
(cm).
(1)求 y 与 x 之间的函数关系式;
(2)求 x 的取值范围;
(3)腰长 AB=3 时,底边的长.
考查题型七 求一元一次方程组中的待定字母的值
1.(2017·内蒙古中考模拟)若不等式组
�� 㐲 � � �
� 㐲 �� �
的解集为﹣1<x<1,那么(a+1)(b﹣1)的值等于_____.
2.(2012·四川中考真题)如果关于 x 的不等式组:
�x-a
≥
�
�x-b
≤
�
,的整数解仅有 1,2,那么适合这个不等式组
的整数 a,b 组成的有序数对(a,b)共有___________个.
3.(2018·四川中考真题)若不等式组
� 㐲 � � �
� 㐲 �� � �
的解集为 1 1x ,则
�� � ��
����
͵
________.
考查题型八 求一元一次方程组中的待定字母的取值范围
1.(2018·山东省寿光世纪学校中考模拟)若不等式组 8 4 1x x
x m
的解集是 x>3,则 m 的取值范围是
( ).
A.m>3 B.m≥3 C.m≤3 D.m<3
2.(2019·四川中考真题)若关于 x 的代等式组
1 02 3
3 5 4 4( 1) 3
x x
x a x a
恰有三个整数解,则 a 的取值范
围是( )
A. 31 2a B. 31 2a C. 31
2
a D. 1a 或 3
2a
3.若关于 x 的一元一次不等式组 x 2m<0
x m>2
有解,则 m 的取值范围为( )
A. 2m> 3
B. 2m 3
C. 2m> 3 D. 2m 3
知识点四 列一元一次不等式(组)解应用题
列一元一次不等式(组)解应用题的一般步骤:
(1)审:认真审题,分清已知量、未知量及其关系,找出题中不等关系,要抓住题设中的关键“字眼”,
如“大于”“小于”“不小于”“不大于”“至少”“最多”等.
(2)设:设出适当的未知数,并用含未知数的代数式表示出题目中涉及的量.
(3)列:根据题中的不等关系,列出不等式.
(4)解:解出所列不等式的解集.
(5)验:检验答案是否符合题意.
(6)答:写出答案.
在以上步骤中,审题是基础,根据题意找出不等关系是关键,而根据不等关系列出不等式又是解题难
点.以上过程可简单表述为: 分析 求解
抽象 检验问题 不等式 解答 .
【考查题型汇总】
考查题型九 利用一元一次不等式(组)解决实际问题的方法
1.(2019·湖北中考真题)某县有 A、B 两个大型蔬菜基地,共有蔬菜 700 吨.若将 A 基地的蔬菜全部运往甲
市所需费用与 B 基地的蔬菜全部运往甲市所需费用相同.从 A、B 两基地运往甲、乙两市的运费单价如下表:
(1)求 A、B 两个蔬菜基地各有蔬菜多少吨?
(2)现甲市需要蔬菜 260 吨,乙市需要蔬菜 440 吨.设从 A 基地运送 m 吨蔬菜到甲市,请问怎样调运可使
总运费最少?
2.(2019·辽宁中考模拟)某图书馆计划选购甲、乙两种图书.已知甲图书每本价格是乙图书每本价格的 2.5
倍,用 800 元单独购买甲图书比用 800 元单独购买乙图书要少 24 本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的 2 倍多 8 本,且用于购买甲、乙两种图书的
总经费不超过 1060 元,那么该图书馆最多可以购买多少本乙图书?
考查题型十 方程组与不等式组相结合解决实际问题
1.(2018·山东中考模拟)今年 3 月 12 日植树节期间,学校预购进 A,B 两种树苗.若购进 A 种树苗 3 棵,
B 种树苗 5 棵,需 2100 元;若购进 A 种树苗 4 棵,B 种树苗 10 棵,需 3800 元.
(1)求购进 A,B 两种树苗的单价;
(2)若该学校准备用不多于 8000 元的钱购进这两种树苗共 30 棵,求 A 种树苗至少需购进多少棵.
2.(2019·湖南中考模拟)东东玩具商店用 500 元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,
接着又用 900 元购进第二批这种悠悠球,所购数量是第一批数量的 1.5 倍,但每套进价多了 5 元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于 25%,那么每套悠悠球的售价至少是多
少元?
考查题型十一 利用不等式计算获利问题
1.(2014·四川中考真题)某商家计划从厂家采购空调和冰箱两种产品共 20 台,空调的采购单价 y1(元/台)
与采购数量 x1(台)满足 y1=﹣20x1+1500(0<x1≤20,x1 为整数);冰箱的采购单价 y2(元/台)与采购数量
x2(台)满足 y2=﹣10x2+1300(0<x2≤20,x2 为整数).
(1)经商家与厂家协商,采购空调的数量不少于冰箱数量的 ,且空调采购单价不低于 1200 元,问该商
家共有几种进货方案?
(2)该商家分别以 1760 元/台和 1700 元/台的销售单价售出空调和冰箱,且全部售完.在(1)的条件下,
问采购空调多少台时总利润最大?并求最大利润.
2.(2018·四川中考模拟)宜兴某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是 200
元/台.经过市场销售后发现:在一个月内,当售价是 400 元/台时,可售出 200 台,且售价每降低 10 元,
就可多售出 50 台.若供货商规定这种空气净化器售价不能低于 300 元/台,代理销售商每月要完成不低于
450 台的销售任务.
(1)试确定月销售量 y(台)与售价 x(元/台)之间的函数关系式;并求出自变量 x 的取值范围;
(2)当售价 x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润 w(元)最大?最大利润
是多少?
3.(2018·山东中考模拟)今年义乌市准备争创全国卫生城市,某小区积极响应,决定在小区内安装垃圾分
类的温馨提示牌和垃圾箱,若购买 2 个温馨提示牌和 3 个垃圾箱共需 550 元,且垃圾箱的单价是温馨提示
牌单价的 3 倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放 48 个垃圾箱,如果购买温馨提示牌和垃圾箱共 100 个,且费用不超过 10000 元,
请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
考查题型十二 运用一元一次不等式组进行方案设计
1.(2018·河南中考模拟)某校计划购买篮球、排球共 20 个.购买 2 个篮球,3 个排球,共需花费 190 元;
购买 3 个篮球的费用与购买 5 个排球的费用相同.
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于 8 个,所需费用总额不超过 800 元.请你求出满足要求的所有购买方案,并直接写
出其中最省钱的购买方案.
2.(2019·广西中考模拟)某文化商店计划同时购进 A、B 两种仪器,若购进 A 种仪器 2 台和 B 种仪器 3 台,
共需要资金 1700 元;若购进 A 种仪器 3 台,B 种仪器 1 台,共需要资金 1500 元.
(1)求 A、B 两种型号的仪器每台进价各是多少元?
(2)已知 A 种仪器的售价为 760 元/台,B 种仪器的售价为 540 元/台.该经销商决定在成本不超过 30000
元的前提下购进 A、B 两种仪器,若 B 种仪器是 A 种仪器的 3 倍还多 10 台,那么要使总利润不少于 21600
元,该经销商有哪几种进货方案?
3.(2019·贵州中考真题)某校计划组织 240 名师生到红色教育基地开展革命传统教育活动.旅游公司有 A,
B 两种客车可供租用,A 型客车每辆载客量 45 人,B 型客车每辆载客量 30 人.若租用 4 辆 A 型客车和 3 辆
B 型客车共需费用 10700 元;若租用 3 辆 A 型客车和 4 辆 B 型客车共需费用 10300 元.
(1)求租用 A,B 两型客车,每辆费用分别是多少元;
(2)为使 240 名师生有车坐,且租车总费用不超过 1 万元,你有哪几种租车方案?哪种方案最省钱?