- 2021-02-26 发布 |
- 37.5 KB |
- 5页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版数学七年级下册《用坐标表示平移》练习题4
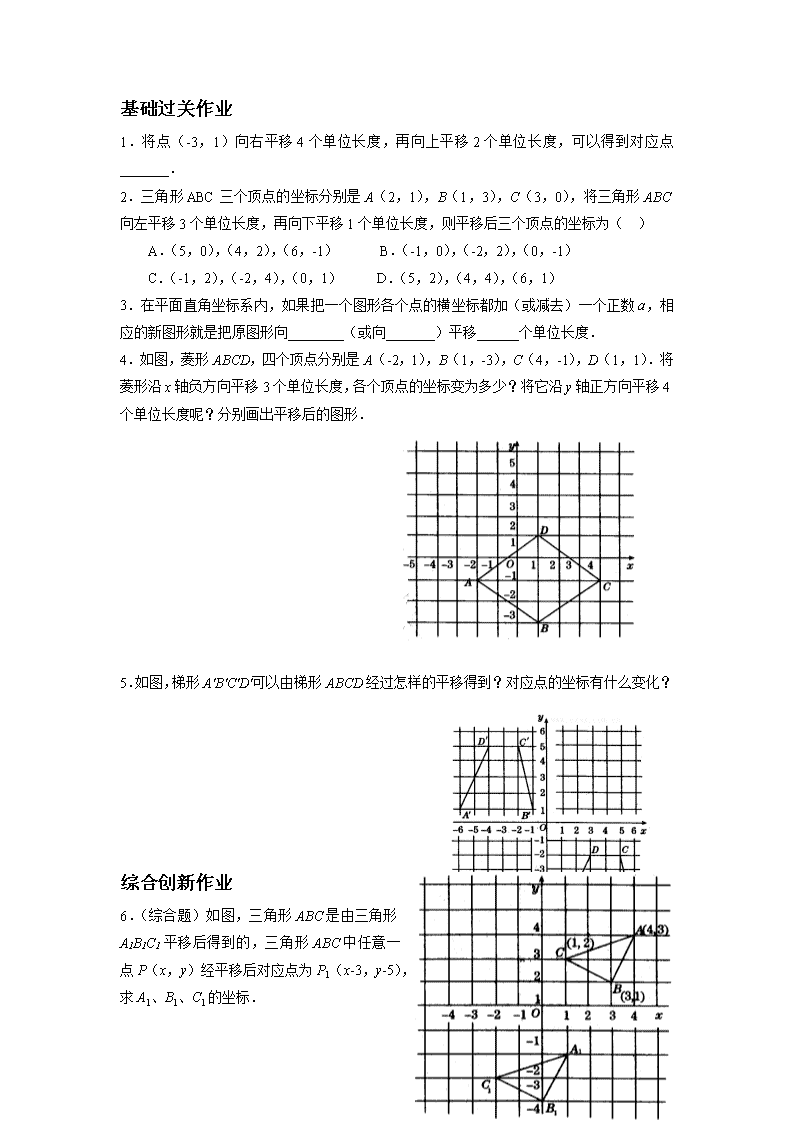
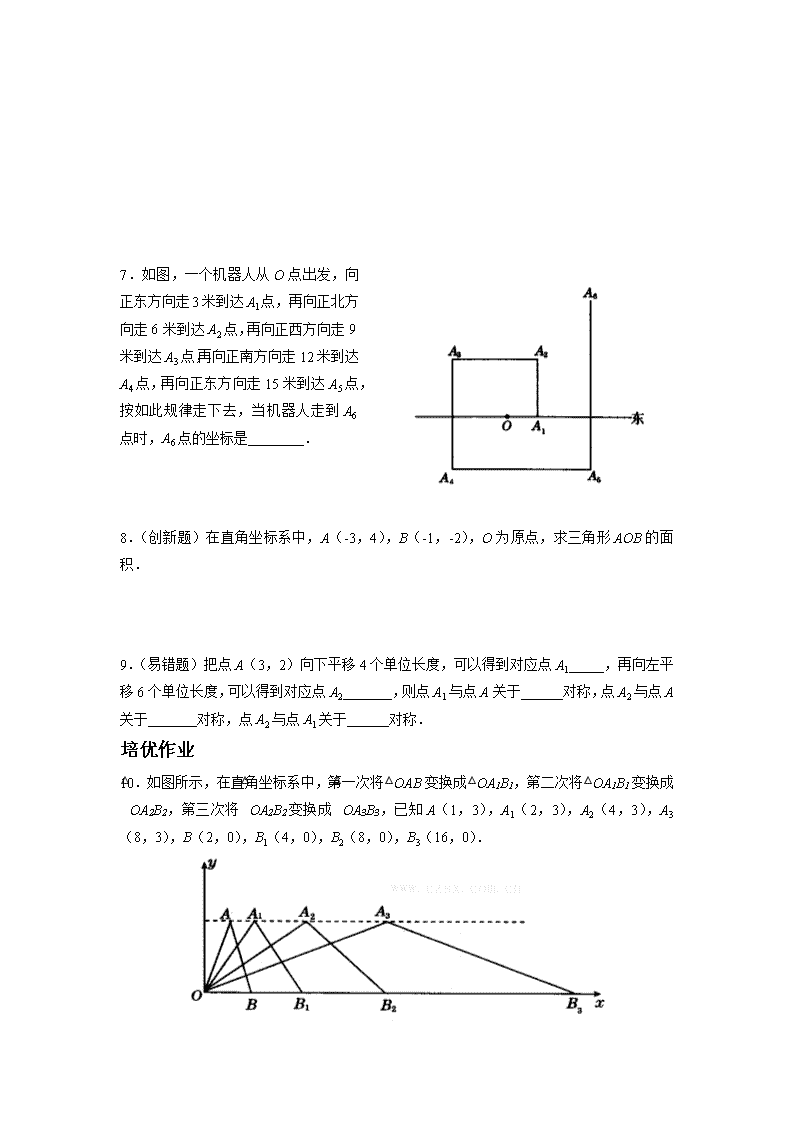
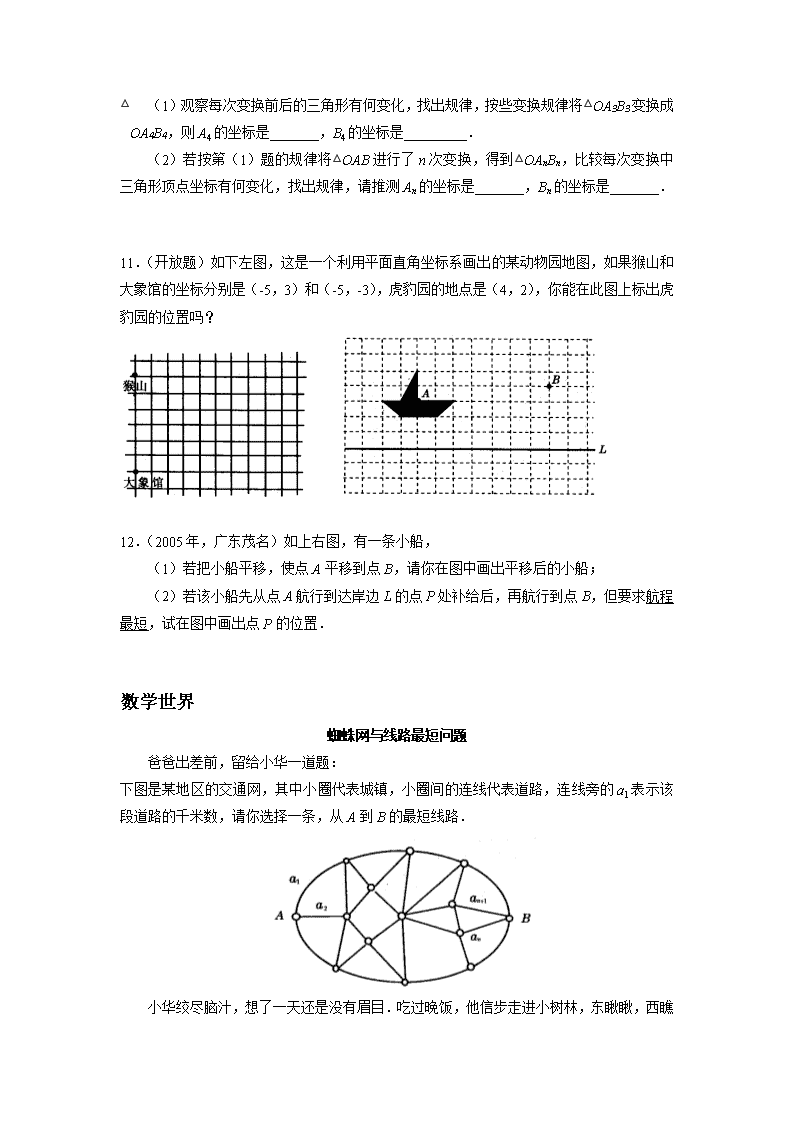
基础过关作业 1.将点(-3,1)向右平移 4 个单位长度,再向上平移 2 个单位长度,可以得到对应点_______. 2.三角形 ABC 三个顶点的坐标分别是 A(2,1),B(1,3),C(3,0),将三角形 ABC 向左平移 3 个单位长度,再向下平移 1 个单位长度,则平移后三个顶点的坐标为( ) A.(5,0),(4,2),(6,-1) B.(-1,0),(-2,2),(0,-1) C.(-1,2),(-2,4),(0,1) D.(5,2),(4,4),(6,1) 3.在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数 a,相 应的新图形就是把原图形向________(或向_______)平移______个单位长度. 4.如图,菱形 ABCD,四个顶点分别是 A(-2,1),B(1,-3),C(4,-1),D(1,1).将 菱形沿 x 轴负方向平移 3 个单位长度,各个顶点的坐标变为多少?将它沿 y 轴正方向平移 4 个单位长度呢?分别画出平移后的图形. 5.如图,梯形 A′B′C′D′可以由梯形 ABCD 经过怎样的平移得到?对应点的坐标有什么变化? 综合创新作业 6.(综合题)如图,三角形 ABC 是由三角形 A1B1C1 平移后得到的,三角形 ABC 中任意一点 P(x,y)经平移后对应点为 P1(x-3,y-5), 求 A1、B1、C1 的坐标. 7.如图,一个机器人从 O 点出发,向 正东方向走 3 米到达 A1 点,再向正北方 向走 6 米到达 A2 点,再向正西方向走 9 米到达 A3 点,再向正南方向走 12 米到 达 A4 点,再向正东方向走 15 米到达 A5 点,按如此规律走下去,当机器人走到 A6 点时,A6 点的坐标是________. 8.(创新题)在直角坐标系中,A(-3,4),B(-1,-2),O 为原点,求三角形 AOB 的面积. 9.(易错题)把点 A(3,2)向下平移 4 个单位长度,可以得到对应点 A1_____,再向左平 移 6 个单位长度,可以得到对应点 A2_______,则点 A1 与点 A 关于______对称,点 A2 与点 A 关于_______对称,点 A2 与点 A1 关于______对称. 培优作业 10.如图所示,在直角坐标系中,第一次将△OAB 变换成△OA1B1,第二次将△OA1B1 变换 成△OA2B2,第三次将△OA2B2 变换成△OA3B3,已知 A(1,3),A1(2,3),A2(4,3), A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0). (1)观察每次变换前后的三角形有何变化,找出规律,按些变换规律将△OA3B3 变换 成△OA4B4,则 A4 的坐标是_______,B4 的坐标是_________. (2)若按第(1)题的规律将 △ OAB 进行了 n 次变换,得到△OAnBn,比较每次变换中 三角形顶点坐标有何变化,找出规律,请推测 An 的坐标是_______,Bn 的坐标是_______. 11.(开放题)如下左图,这是一个利用平面直角坐标系画出的某动物园地图,如果猴山和 大象馆的坐标分别是(-5,3)和(-5,-3),虎豹园的地点是(4,2),你能在此图上标出虎 豹园的位置吗? 12.(2005 年,广东茂名)如上右图,有一条小船, (1)若把小船平移,使点 A 平移到点 B,请你在图中画出平移后的小船; (2)若该小船先从点 A 航行到达岸边 L 的点 P 处补给后,再航行到点 B,但要求航程 最短,试在图中画出点 P 的位置. 数学世界 蜘蛛网与线路最短问题 爸爸出差前,留给小华一道题: 下图是某地区的交通网,其中小圈代表城镇,小圈间的连线代表道路,连线旁的 a1 表示该 段道路的千米数,请你选择一条,从 A 到 B 的最短线路. 小华绞尽脑汁,想了一天还是没有眉目.吃过晚饭,他信步走进小树林,东瞅瞅,西瞧 瞧,一眼落到一张硕大的蜘蛛网上,这张蜘蛛网,多像那张交通图啊!突然,一只小虫撞到 网上,小虫奋力挣扎,于是便不断地拉紧连到网中心的最短的那根丝,蜘蛛沿着那根丝,迅 速出击,抓住了小虫,小华若有所悟,口里直嚷嚷:“有了!有了!”很快地解出了这道题, 你知道小华是用什么方法解决这道题的吗? 答案: 1.(1,3) 2.B 点拨:将 A、B、C 三点的横坐标都减去 3,纵坐标都减去 1 得(-1,0),(-2,2), (0,-1),故选 B. 3.右;左;a 4.解:将菱形沿 x 轴负方向平移 3 个单位长度,各个顶点的坐标变为 (-5,-1),(-2,-3),(1,-1),(-2,1). 将它沿 y 轴正方向平移 4 个单位长度,各个顶点的坐标变为 (-2,3),(1,1),(4,3),(1,5).图略. 5.解:梯形 A′B′C′D′可以由梯形 ABCD 先向左平移 7 个单位,再向上平移 7 个单位得到.点 A、B、C、D 的横坐标都减去 7,纵坐标都加 7,可以得到点 A′、B′、C′、D′的坐标. A(1,-6)→A′(-6,1),B(6,-6)→B′(-1,1),C(5,-2)→C′(-2,5),D(3, -2)→D′(-4,5). 6.解:由题意知,三角形 A1B1C1 是由三角形 ABC 先向左平移 3 个单位长度,再向下平移 5 个单位长度得到的. 因为 A(4,3),B(3,1),C(1,2) 所以 A1(1,-2),B1(0,-4),C1(-2,-3). 7.解:以点 O 为原点,正向方向为 x 轴正方向, 正北方向为 y 轴正方向,建立如答图所示的平面 直角坐标系,题中机器人运动的过程,实质上是 坐标系中点的平移过程,即 A1(3,0)→A2(3, 6)→A3(-6,6)→A4(-6,-6)→A5(9,-6) →A6(9,12). 因此,在以 O 点为坐标原点,正北方向为 y 轴正 方向的平面坐标系中,A6 的坐标为(9,12). 8.解:如答图,作 AC⊥y 轴,BD⊥y 轴,垂足分别为 C、 D. ∵A(-3,4),B(-1,-2), ∴AC=3,BD=1,CD=6,OD=2 ∴S△AOB=S 梯形 ABCD-(S△OAC+S△OBD) = 1 2 ×(1+3)×6-( 1 2 ×3×4+ 1 2 ×1×2)=5. 点拨:在平面直角坐标系中求几何图形的面积,通常采取向 x 轴或 y 轴作垂线,将几何 图形割补的方法,同学们想一想,这是为什么? 9.(3,-2);(-3,-2);x 轴;原点;y 轴 点拨:点(a,b)关于 x 轴的对称点是(a,-b),关于 y 轴的对称点是(-a,b),关于 原点的对称点是(-a,-b). 10.(1)(16,3);(32,0) 点拨:A(1,3),A1(2,3),A2(4,3),A3(8,3),其纵坐标都为 3, 而横坐标依次为 20,21,22,23.因此,A4(24,3),即 A4(16,3). 同理,B(2,0),B1(4,0),B2(8,0),B3(16,0),它们的纵坐标都是 0, 而横坐标依次是 21,22,23,24,因此得出 B4(24+1,0),即 B4(32,0). (2)(2n,3);(2n+1,0) 11.如答图: 点拨:首先确定出平面直角坐标系的原点,x 轴、y 轴的正方向. 12.解:(1)平移后的小船如答图所示. (2)如答图,点 A′与点 A 关于直线 L 成轴对称,连接 A′B 交直线 L 于点 P,则点 P 为所求.查看更多