福建专版2020中考数学复习方案第六单元圆第32课时直线与圆的位置关系课件
第 32 课时
直线与圆的位置关系
第六单元 圆
基
础
知
识
巩
固
高
频
考
向
探
究
如果圆的半径是r,点到圆心的距离是d,那么
点在圆外⇔①
点在圆上⇔②
点在圆内⇔③
考点一 点和圆的位置关系
考点聚焦
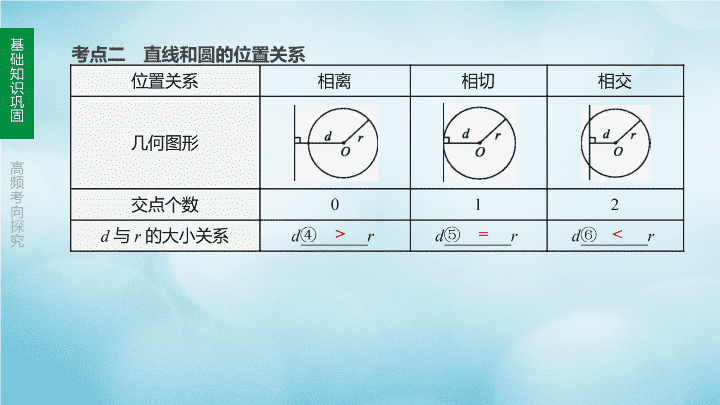
d>r
d=r
d
= <
基
础
知
识
巩
固
高
频
考
向
探
究
切线的性质 圆的切线⑦ 过切点的半径
推论
(1)经过圆心且垂直于切线的直线必过⑧
(2)经过切点且垂直于切线的直线必过⑨
切线的判定
(1)和圆只有⑩ 公共点的直线是圆的切线
(2)如果圆心到一条直线的距离等于圆的⑪ ,那么这条直线是
圆的切线
(3)经过半径的外端并且⑫ 这条半径的直线是圆的切线
常添辅助线 连接圆心和切点
考点三 切线的性质与判定
垂直于
切点
圆心
一个
半径
垂直于
基
础
知
识
巩
固
高
频
考
向
探
究
证圆的切线的技巧:
(1)有公共点,连半径,证垂直;
(2)无公共点,作垂直,证半径.
基
础
知
识
巩
固
高
频
考
向
探
究
切线长
经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的
切线长
切线长定理
从圆外一点可以引圆的两条切线,它们的切线长⑬ ,这一点和圆
心的连线⑭ 两条切线的夹角
基本图形
如图所示,点P是☉O外一点,PA,PB分别切☉O于点
A,B,AB交PO于点C,则有如下结论:
(1)PA=PB;
(2)∠APO=∠BPO=∠OAC=∠OBC,∠AOP=∠BOP=
∠CAP=∠CBP
考点四 切线长与切线长定理
相等
平分
基
础
知
识
巩
固
高
频
考
向
探
究
外接圆 内切圆
图形
定义 经过三角形的三个顶点的圆 与三角形各边都相切的圆
圆心O
外心(三角形三条边的
⑮ 的交点)
内心(三角形三个内角的⑯ 的
交点)
性质
三角形的外心到三角形的三个
顶点的距离相等
三角形的内心到三角形的三条边的距离
相等
考点五 三角形的外接圆与内切圆
垂直平分线
角平分线
基
础
知
识
巩
固
高
频
考
向
探
究
(续表)
外接圆 内切圆
画法
作三角形任意两边的垂直平分
线,其交点即为圆心O,以圆心O到
任一顶点的距离为半径作☉O即可
作三角形任意两角的平分线,其交点即
为圆心O,过点O作任一边的垂线段作为半
径,作☉O即可
基
础
知
识
巩
固
高
频
考
向
探
究
图32-1
基
础
知
识
巩
固
高
频
考
向
探
究
题组一 必会题
对点演练
1.如图32-2,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,3为半径的圆与直线
OA的位置关系是 ( )
A.相离 B.相交
C.相切 D.以上三种情况均有可能
C
图32-2
基
础
知
识
巩
固
高
频
考
向
探
究
2.[2019·苏州]如图32-3,AB为☉O的切线.
切点为A,连接AO,BO,BO与☉O交于点C,
延长BO与☉O交于点D,连接AD.若
∠ABO=36°,则∠ADC的度数为 ( )
A.54° B.36°
C.32° D.27°
图32-3
[答案]D
基
础
知
识
巩
固
高
频
考
向
探
究
3.[2019·厦门质检]命题:直角三角形的一条直角边与以另一条直角边为直径的
圆相切.符合该命题的图形是 ( )
图32-4
C
基
础
知
识
巩
固
高
频
考
向
探
究
4.[2019·莆田质检]如图32-5,AB,AC均为☉O的切线,切点分别为B,C,点D是优弧
BC上一点,则下列关系式中,一定成立的是 ( )
A.∠A+∠D=180°
B.∠A+2∠D=180°
C.∠B+∠C=270°
D.∠B+2∠C=270° 图32-5
B
基
础
知
识
巩
固
高
频
考
向
探
究
5.如图32-6,AB是☉O的直径,C,D是☉O上的点,∠CDB=20°,过点C作☉O的切线交
AB的延长线于点E,则∠E= .
图32-6
50°
基
础
知
识
巩
固
高
频
考
向
探
究
题组二 易错题
【失分点】
定义法判定直线和圆的位置关系和d,r比较法判定直线和圆的位置关系相互混淆;
切线的性质是知切线得垂直,切线的判定是知垂直得切线,应用中勿混淆;切线长
定理掌握得一知半解,导致做题过程复杂;混淆三角形的内心和外心.
6.如图32-7,已知☉O的半径为5,直线EF经过☉O上一点P(点E,F在点P的两旁),下
列条件能判定直线EF与☉O相切的是 ( )
A.OP=5 B.OE=OF
C.O到直线EF的距离是4 D.OP⊥EF
D
图32-7
基
础
知
识
巩
固
高
频
考
向
探
究
A
图32-8
8.已知在△ABC中,∠C=90°,AC=4,BC=3,点O为△ABC的内心,则OC= .
基
础
知
识
巩
固
高
频
考
向
探
究
考向一 直线与圆的位置关系
[答案] A
[解析]设圆的半径为r,点O到直线l
的距离为d,
∵d=5,r=6,∴dDB
C.DI
查看更多