- 2021-02-26 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019年高考数学总复习检测第49讲 空间点、线、面的位置关系
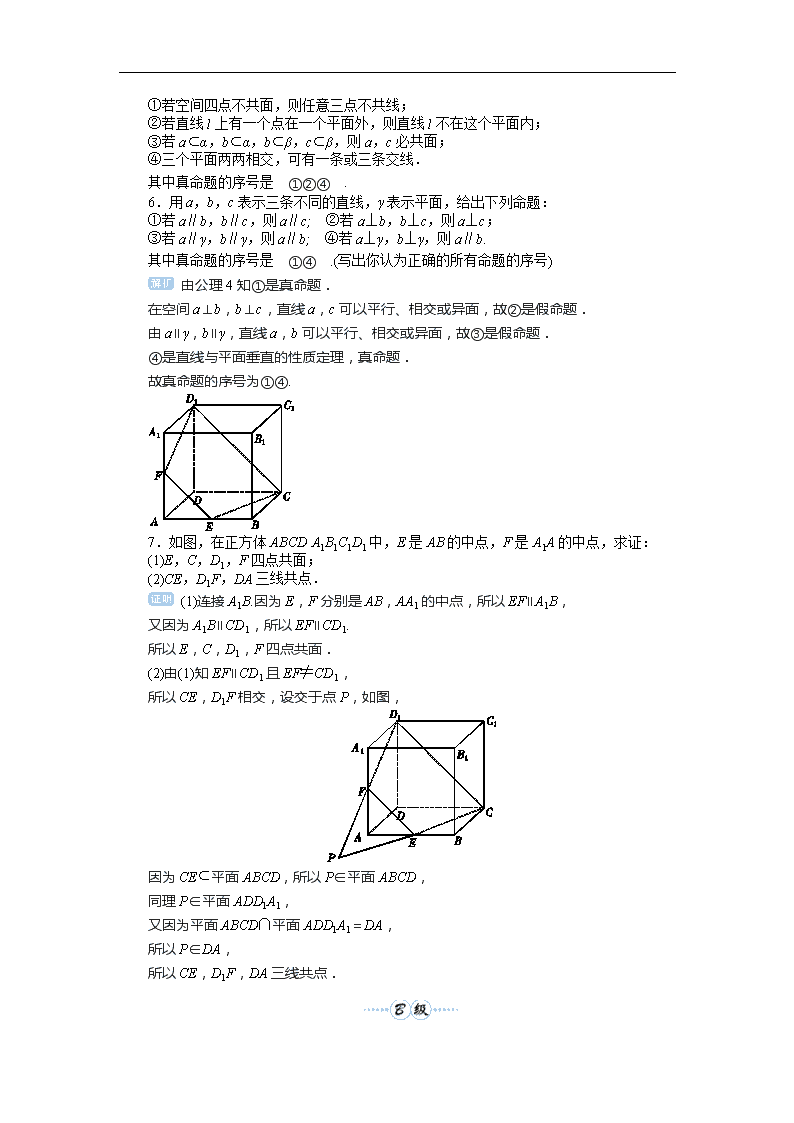
第49讲 空间点、线、面的位置关系 1.下列命题正确的个数是(B) ①如果一个角的两边与另一个角的两边分别平行,那么这两个角相等; ②如果两条相交直线与另两条直线分别平行,那么这两组直线所成的锐角或直角相等; ③如果一个角的两边与另一个角的两边分别垂直,那么这两个角相等或互补; ④如果两条直线同时平行于第三条直线,那么这两条直线互相平行. A.1个 B.2个 C.3个 D.4个 ①中两角应相等或互补;②的说法正确,因为两直线所成的角即夹角为锐角或直角;③在平面几何中成立,但在立体几何中不一定成立;④根据平行公理,是正确的.因此②④是正确的. 2.(2017·哈尔滨模拟)已知a,b,c是空间中的三条不同的直线,命题p:若a⊥b,a⊥c,则b∥c;命题q:若直线a,b,c两两相交,则a,b,c共面,则下列命题中为真命题的是(D) A.p∧q B.p∨q C.(綈p)∧q D.p∨(綈q) 若a⊥b,a⊥c,则b,c可能平行,也可能相交,还可能异面,所以命题p是假命题. 若直线a,b,c交于三个不同的点时,三条直线一定共面,当三条直线交于一点时,三条直线不一定共面,所以命题q也是假命题. 故p∨(綈q)为真命题. 3.(2016·广州市高考模拟)已知E,F,G,H是空间四点,命题甲:E,F,G,H四点不共面,命题乙:直线EF和GH不相交,则甲是乙成立的(B) A.必要不充分条件 B.充分不必要条件 C.充要条件 D.既不充分也不必要条件 甲⇒乙,但乙⇒/ 甲,所以甲是乙成立的充分不必要条件. 4.如图,空间四边形ABCD中,对角线AC⊥BD,E、F、G、H分别为边AB、BC、CD、DA的中点,则四边形EFGH的形状一定是(C) A.等腰梯形 B.菱形 C.矩形 D.正方形 因为E、F、G、H分别为边AB、BC、CD、DA的中点, 所以EF綊AC,GH綊AC, 所以EF綊GH,所以四边形EFGH为平行四边形. 又AC⊥BD,而EF∥AC,GF∥BD,所以EF⊥FG. 故四边形EFGH为矩形. 5.有下面几个命题: ①若空间四点不共面,则任意三点不共线; ②若直线l上有一个点在一个平面外,则直线l不在这个平面内; ③若a⊂α,b⊂α,b⊂β,c⊂β,则a,c必共面; ④三个平面两两相交,可有一条或三条交线. 其中真命题的序号是 ①②④ . 6.用a,b,c表示三条不同的直线,γ表示平面,给出下列命题: ①若a∥b,b∥c,则a∥c; ②若a⊥b,b⊥c,则a⊥c; ③若a∥γ,b∥γ,则a∥b; ④若a⊥γ,b⊥γ,则a∥b. 其中真命题的序号是 ①④ .(写出你认为正确的所有命题的序号) 由公理4知①是真命题. 在空间a⊥b,b⊥c,直线a,c可以平行、相交或异面,故②是假命题. 由a∥γ,b∥γ,直线a,b可以平行、相交或异面,故③是假命题. ④是直线与平面垂直的性质定理,真命题. 故真命题的序号为①④. 7.如图,在正方体ABCDA1B1C1D1中,E是AB的中点,F是A1A的中点,求证: (1)E,C,D1,F四点共面; (2)CE,D1F,DA三线共点. (1)连接A1B.因为E,F分别是AB,AA1的中点,所以EF∥A1B, 又因为A1B∥CD1,所以EF∥CD1. 所以E,C,D1,F四点共面. (2)由(1)知EF∥CD1且EF≠CD1, 所以CE,D1F相交,设交于点P,如图, 因为CE⊂平面ABCD,所以P∈平面ABCD, 同理P∈平面ADD1A1, 又因为平面ABCD∩平面ADD1A1=DA, 所以P∈DA, 所以CE,D1F,DA三线共点. 8.(2017·河南六市一模)设直线m,n是两条不同的直线,α,β是两个不同的平面,下列事件中是必然事件的是(D) A.若m∥α,n∥β,m⊥n,则α⊥β B.若m∥α,n⊥β,m∥n,则α∥β C.若m⊥α,n∥β,m⊥n,则α∥β D.若m⊥α,n⊥β,m∥n,则α∥β 对于A,m∥α,n∥β,m⊥n,则α与β可能平行,也可能相交,所以A不是必然事件; 对于B,m∥α,n⊥β,则m⊥β,又m∥α,则α⊥β,所以B是不可能事件; 对于C,m⊥α,n∥β,m⊥n,则α与β可能平行,所以C不是必然事件; 对于D,m⊥α,m∥n,则n⊥α,又n⊥β,所以α∥β,因此D是必然事件. 9.若α,β是两个相交平面,则在下列命题中,真命题的序号是 ②④ .(写出所有真命题的序号) ① 若直线m⊥α,则在平面β内,一定不存在与直线m平行的直线; ②若直线m⊥α,则在平面β内,一定存在无数条直线与直线m垂直; ③若直线m⊂α,则在平面β内,不一定存在与直线m垂直的直线; ④若直线m⊂α,则在平面β内,一定存在与直线m垂直的直线. 对于①,若直线m⊥α,如果α⊥β,则在平面β内,存在与直线m平行的直线,故①错误; 对于②,若直线m⊥α,则直线m垂直于平面α内的所有直线,则直线m垂直于α,β的交线.在平面β内,存在无数条与交线平行的直线,这无数条直线与直线m垂直,故②正确; 对于③④,若直线m⊂α,则在平面β内,一定存在与直线m垂直的直线,故③错误,④正确. 10.如图所示,在空间四边形ABCD中,E、H分别是边AB、AD上的点,且==,F、G分别是边CB、CD上的点,且==.求证:四边形EFGH是梯形. 在△ABD中,==, 所以EH∥BD,且EH=BD. 在△BCD中,==, 所以FG∥BD,且FG=BD. 根据平行公理知,FG∥EH. 又因为FG>EH,所以四边形EFGH是梯形.查看更多