- 2021-02-26 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
相似三角形中考复习学案
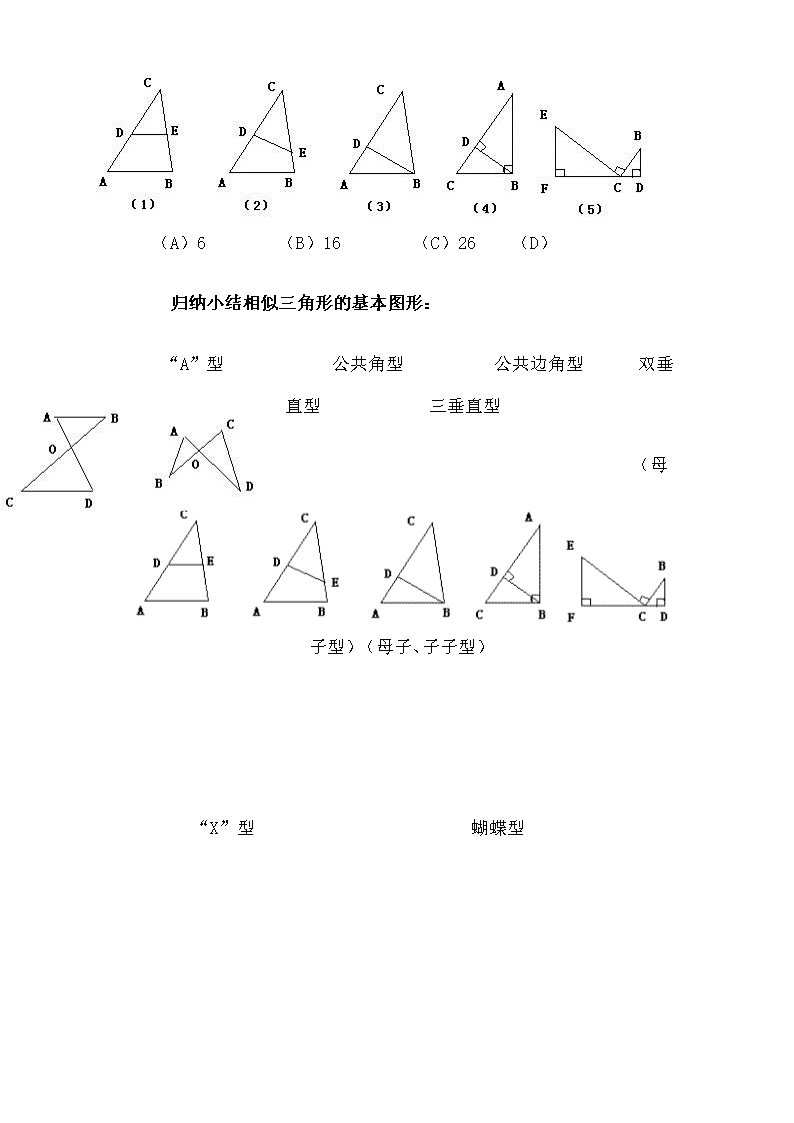
相似三角形----中考复习学案 学习目标: 1.复习巩固想似三角形的概念、性质和判定方法,使学生能够熟练地利用相似三角形知识进行简单证明,掌握综合法证明的表达格式。 2.通过对图形的观察和分析,鼓励学生探索并发现规律,培养学生的探究意识和能力。 3.渗透图形变换和转化等数学思想,引导学生拓展思维空间,提升解题能力。 4、通过变式训练让学生感受图形从一般到特殊的变化;感受到题目的多解性;提高培养学生分析问题、解决问题的能力 学习重点:运用相似三角形的性质和判定,证明简单的几何问题,规范综合法证明的格式。 学习难点:引导学生通过添加辅助线构造相似三角形解决综合问题。 一、情境: (2009年衡阳市)如图,矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,则AG的长为( ) A.1 B. C. D.2 (检查学生做的情况,大部分学生利用勾股定理计算。) 这道题目也可以利用相似三角形来计算。有时利用相似三角形解决问题较简便。今天我们复习相似三角形。(出示课题) 二、 梳理相似三角形基本图形: 在我们学习相似三角形这一章时同学们做了许多题目,今天我们来回顾一下,看看他们之间有没有联系,同时检验一下同学们对图形的感觉。 1、如图(1),已知CA=8,CB=6,AB=5,CD=4 (1)若CE= 3,则DE=____ (2)如图(2)若CE= ,则DE=____. 2、如图(3),在⊿ABC中,D为AC边上一点,∠DBC=∠A,BC= ,AC=3,则CD的长为( ) (A)1 (B)2 (C) (D) 3、如图(4),∠ABC=90, BD⊥AC于D,DC=4,AD=9,则BD的长为( ) (A)36 (B)16 (C)6 (D) 4、如图,F、C、D共线,BD⊥FD, EF⊥FD,BC⊥EC ,若DC=2,BD=3,FC=9,则EF的长为( ) (A)6 (B)16 (C)26 (D) 归纳小结相似三角形的基本图形: “A”型 公共角型 公共边角型 双垂直型 三垂直型 (母子型)(母子、子子型) “X”型 蝴蝶型 (老师在黑板上逐一画出基本图形) 三、学生探究: 1、在△ABC中,AB>AC,过AB上一点D作直线DE交另一边于E,使所得三角形与原三角形相似,画出满足条件的图形. 变式:在Rt△ABC中,∠C=90埃 ?SPAN>AB上一点D作直线DE交另一边于E,使所得三角形与原三角形相似,画出满足条件的图形. (先让学生在下面画,再让一个学生上黑板画、其他学生上黑板补充) 让学生感受图形从一般到特殊变化时,题目的答案从四解减少到三解。 2.如图,在矩形ABCD中,E在AD上,EF⊥BE,交CD于F,连结BF,则图中与△ABE一定相似的三角形是( ) A.△EFB B.△DEF C.△CFB D.△EFB和△DEF 变式:如图,在矩形ABCD中,E在AD上,EF⊥BE,交CD于F,连结BF,若使图中△BEF与△ABE相似,需添加条件: 。 (让学生感受三垂直型) 3.如图,在矩形ABCD中,AB=4,AD=10,点P在BC边上,若△ABP与△DCP相似。△APD一定是( ) (A)直角三角形 (B)等腰三角形 (C)等腰直角三角形 (D)等腰三角形或直角三角形 变式:如图,在矩形ABCD中,AB=4,AD=10,若点P在BC边上,则△ABP与△DCP相似的点P有 个。 (进一步让学生感受“三垂直型”,并提醒学生注意全等三角形是特殊的相似三角形) 四、拓展: 1、梯形ABCD中,AD∥BC,AD查看更多