- 2021-02-26 发布 |
- 37.5 KB |
- 48页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考压轴题圆含答案
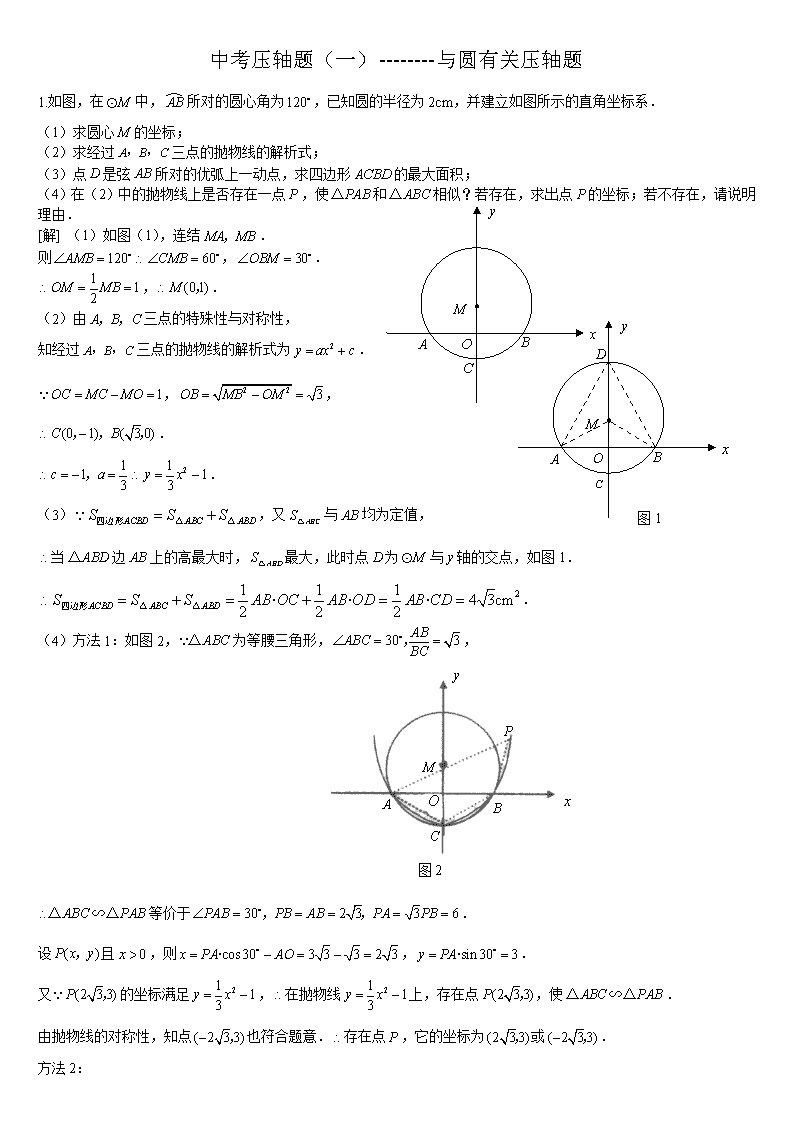
中考压轴题(一)--------与圆有关压轴题 1.如图,在中,所对的圆心角为,已知圆的半径为2cm,并建立如图所示的直角坐标系. (1)求圆心的坐标; (2)求经过三点的抛物线的解析式; (3)点是弦所对的优弧上一动点,求四边形的最大面积; (4)在(2)中的抛物线上是否存在一点,使和相似?若存在,求出点的坐标;若不存在,请说明理由. [解] (1)如图(1),连结. 则,. ,. 图1 (2)由三点的特殊性与对称性, 知经过三点的抛物线的解析式为. ,, . . (3),又与均为定值, 当边上的高最大时,最大,此时点为与轴的交点,如图1. . (4)方法1:如图2,为等腰三角形,, 图2 等价于. 设且,则,. 又的坐标满足,在抛物线上,存在点,使. 由抛物线的对称性,知点也符合题意.存在点,它的坐标为或. 方法2: 如图(3),当时,,又由(1)知, 点在直线上. 设直线的解析式为, 将代入,解得直线的解析式为. 解方程组得. 又,.,. 在抛物线上,存在点,使. 由抛物线的对称性,知点也符合题意.存在点,它的坐标为或. 方法3: 如图3,为等腰三角形,且,设则 图3 等价于,. 当时,得解得. 又的坐标满足,在抛物线上,存在点,使. 由抛物线的对称性,知点也符合题意.存在点,它的坐标为或. [点评]本题是一道综合性很强也是传统型的压轴题,涉及了函数、方程、相似、圆等大量初中数学的重点知识,解这类问题要求学生必须稳固的掌握各个领域的数学知识,须注意的是在第4小问中涉及了相似三角形的问题,很有可能会有多解的情况出现,此时就要求学生拥有较强的数形结合思想去探索结论的存在性。 2.(06湖南湘潭卷)已知:如图,抛物线的图象与轴分别交于两点,与轴交于点,经过原点及点,点是劣弧上一动点(点与不重合). (1)求抛物线的顶点的坐标; (2)求的面积; (3)连交于点,延长至,使,试探究当点运动到何处时,直线与相切,并请说明理由. [解] (1)抛物线 的坐标为 (2)连;过为的直径. 而 (3)当点运动到的中点时,直线与相切 理由:在中,. 点是的中点 , 在中,为等边三角形 又为直径,当为的中点时,为的切线 [点评]本题将抛物线与圆放在同一坐标系中研究,因此数形结合的解题思想是不可缺少的,解第3小问时可以先自己作图来确定D点的位置。 3.(06湖南永州卷)如图,以为圆心的两个同心圆中,大圆的直径交小圆于两点,大圆的弦切小圆于点,过点作直线,垂足为,交大圆于两点. (1)试判断线段与的大小关系,并说明理由. (2)求证:. (3)若是方程的两根(),求图中阴影部分图形的周长. A B C D E O N H M F [解] (1)相等. 连结,则,故. (2)由,得, 又由,得. . (3)解方程得:,, ,, 在中,,,. 在中,, ,, 弧长,, 阴影部分周长. [点评]本题是比较传统的几何型综合压轴题,涉及圆、相似、三角等几何重点知识。 4. (06辽宁卷)如图,已知,以点为圆心,以长为半径的圆交轴于另一点,过点作交于点,直线交轴于点. (1)求证:直线是的切线; (2)求点的坐标及直线的解析式; x y A B C O F E (3)有一个半径与的半径相等,且圆心在轴上运动的.若与直线相交于两点,是否存在这样的点,使是直角三角形.若存在,求出点的坐标;若不存在,请说明理由. [解] (1)证明:连结 又 又 是的切线. (2)方法①由(1)知 ,, ① 又, ② 由①②解得(舍去)或, 直线经过,两点设的解析式: 解得直线的解析式为. 方法②:切于点, 又,,即 ① 又, ② 由①②解得(舍去)或 (求的解析式同上). 方法③, ① 切于点,, , ② 由①②解得:, (求的解析式同上). (3)存在; 当点在点左侧时,若,过点作于点, ,, ,,, ,, 当点在点右侧时,设,过点作于点,则 x y A B C O P F M E H N Q 1 2 3 4 ,可知与关于点中心对称, 根据对称性得 存在这样的点,使得为直角三角形, 点坐标或. [点评]本题是一道综合性很强的传统型压轴题,其难度比较恰当,选拔功能较强,解第3小题时要注意分类讨论,这是本题最容易失分的地方 5. (06辽宁沈阳卷)如图,在平面直角坐标系中,直线分别与轴,轴交于点,点. (1)以为一边在第一象限内作等边及的外接圆(用尺规作图,不要求写作法,但要保留作图痕迹); (2)若与轴的另一个交点为点,求,,,四点的坐标; (3)求经过,,三点的抛物线的解析式,并判断在抛物线上是否存在点,使的面积等于的面积?若存在,请直接写出所有符合条件的点的坐标;若不存在,请说明理由. [解] (1)如图,正确作出图形,保留作图痕迹 (2)由直线,求得点的坐标为,点的坐标为 在中,, , 是等边三角形, 点的坐标为,连结 是等边三角形 直线是的切线点的坐标为 (3)设经过,,三点的抛物线的解析式是 把代入上式得抛物线的解析式是 存在点,使的面积等于的面积 点的坐标分别为,. [点评]本题是一道综合性很强的压轴题,主要考查二次函数、一次函数、圆、几何作图等大量知识,第3小题是比较常规的结论存在性问题,运用方程思想和数形结合思想可解决。 6.已知:抛物线与轴相交于两点,且. (Ⅰ)若,且为正整数,求抛物线的解析式;(Ⅱ)若,求的取值范围; (Ⅲ)试判断是否存在,使经过点和点的圆与轴相切于点,若存在,求出的值;若不存在,试说明理由; (Ⅳ)若直线过点,与(Ⅰ)中的抛物线相交于两点,且使,求直线的解析式. [解] (Ⅰ)解法一:由题意得, . 解得,.为正整数,.. 解法二:由题意知,当时,. 以下同解法一) 解法三:, . 又. .(以下同解法一.) 解法四:令,即,.(以下同解法三.) A B x D y O (Ⅱ)解法一:., 即. .解得 的取值范围是. 解法二:由题意知,当时, . 解得:.的取值范围是. 解法三:由(Ⅰ)的解法三、四知,. , .的取值范围是. (Ⅲ)存在. 解法一:因为过两点的圆与轴相切于点,所以两点在轴的同侧,. 由切割线定理知,, 即., . 解法二:连接.圆心所在直线, 设直线与轴交于点,圆心为, 则. , . 在中, . 即.解得 . (Ⅳ)设,则. y x O P Q F 7 过分别向轴引垂线,垂足分别为. 则. 所以由平行线分线段成比例定理知,. 因此,,即. 过分别向轴引垂线,垂足分别为, 则.所以.. .. ,或. 当时,点.直线过, 解得 当时,点.直线过, 解得故所求直线的解析式为:,或. 7. 如图,在平面直角坐标系中,已知点,,以为边在轴下方作正方形,点是线段与正方形的外接圆除点以外的另一个交点,连结与相交于点. (1)求证:; (2)设直线是的边的垂直平分线,且与相交于点.若是的外心,试求经过三点的抛物线的解析表达式; A E O D C B G F x y l (3)在(2)的条件下,在抛物线上是否存在点,使该点关于直线的对称点在轴上?若存在,求出所有这样的点的坐标;若不存在,请说明理由. [解] (1)在和中, 四边形是正方形,. 又, . (2)由(1),有,.点. 是的外心,点在的垂直平分线上.点也在的垂直平分线上.为等腰三角形,. 而,. . 设经过三点的抛物线的解析表达式为. 抛物线过点,.. ① 把点,点的坐标代入①中,得 即 解得 抛物线的解析表达式为. ② (3)假定在抛物线上存在一点,使点关于直线的对称点在轴上.是的平分线, 轴上的点关于直线的对称点必在直线上,即点是抛物线与直线的交点. A E O D C B G F x y l Q 设直线的解析表达式为,并设直线与轴交于点,则由是等腰直角三角形. .. 把点,点代入中,得 直线的解析表达式为. 设点,则有. ③ 把③代入②,得, ,即. .解得或. 当时,;当时,. 在抛物线上存在点,它们关于直线的对称点都在轴上. 8.在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0,),直线l2的函数表达式为,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M. (1) 填空:直线l1的函数表达式是 ,交点P的坐标是 ,∠FPB的度数是 ; (2) 当⊙C和直线l2相切时,请证明点P到直线CM的距离等于⊙C的半径R,并写出R=时a的值. (3) 当⊙C和直线l2不相离时,已知⊙C的半径R=,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由. 2 1 3 4 1 2 3 -1 -2 -3 -1 y x O A B E F P l1 l2 C 图2 N M [解] (1) P(1,) 60º 2 1 3 4 1 2 3 -1 -2 -3 -1 y x O A B E F P l1 l2 C (第24题图甲) G D M (2) 设⊙C和直线l2相切时的一种情况如图甲所示,D是切点,连接CD,则CD⊥PD. 过点P作CM的垂线PG,垂足为G,则Rt△CDP≌Rt△PGC (∠PCD=∠CPG=30º,CP=PC), 所以PG=CD=R. 当点C在射线PA上,⊙C和直线l2相切时,同理可证.取R=时,a=1+R=,或a=-(R-1) (3) 当⊙C和直线l2不相离时,由(2)知,分两种情况讨论: ① 如图乙,当0≤a≤时,, 当时,(满足a≤),S有最大值.此时(或). ② 当≤a<0时,显然⊙C和直线l2相切即时,S最大.此时 . 综合以上①和②,当或时,存在S的最大值,其最大面积为 9. 如图1,已知中,,.过点作,且,连接交于点. (1)求的长; (2)以点为圆心,为半径作,试判断与是否相切,并说明理由; (3)如图2,过点作,垂足为.以点为圆心,为半径作;以点为圆心,为半径作.若和的大小是可变化的,并且在变化过程中保持和相切,且使点在的内部,点在的外部,求和的变化范围. A B C P E E A B C P D 图1 图2 [解] (1)在中,,. ,..,. (2)与相切. 在中,,, ,. 又,与相切. (3)因为,所以的变化范围为. 当与外切时,,所以的变化范围为; 当与内切时,,所以的变化范围为. [点评]本题是一道比较传统的几何综合题,第1题运用相似三角形知识即可得解,第2小题也较基础,第3小题注意要分类,试题中只说明了“和相切”,很多同学漏解往往是由于没有仔细读题和审题。 8,(06江苏宿迁课改卷)设边长为2a的正方形的中心A在直线l上,它的一组对边垂直于直线l,半径为r的⊙O的圆心O在直线l上运动,点A、O间距离为d. (1)如图①,当r<a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表: d、a、r之间关系 公共点的个数 d>a+r 图① d=a+r a-r<d<a+r d=a-r d<a-r 所以,当r<a时,⊙O与正方形的公共点的个数可能有 个; (2)如图②,当r=a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表: d、a、r之间关系 图② 公共点的个数 d>a+r d=a+r a≤d<a+r d<a 所以,当r=a时,⊙O与正方形的公共点个数可能有 个; 图③ (3)如图③,当⊙O与正方形有5个公共点时,试说明r=a; (4)就r>a的情形,请你仿照“当……时,⊙O与正方形的公共点个数可能有 个”的形式,至少给出一个关于“⊙O与正方形的公共点个数”的正确结论. [解] (1) d、a、r之间关系 公共点的个数 d>a+r 0 d=a+r 1 a-r<d<a+r 2 d=a-r 1 d<a-r 0 图① 所以,当r<a时,⊙O与正方形的公共点的个数可能有0、1、2个; 图② (2) d、a、r之间关系 公共点的个数 d>a+r 0 d=a+r 1 a≤d<a+r 2 d<a 4 所以,当r=a时,⊙O与正方形的公共点个数可能有0、1、2、4个; (3)方法一:如图所示,连结OC则OE=OC=r ,OF=EF-OE=2a-r. B C D F E 在Rt△OCF中,由勾股定理得: OF2+FC2=OC2 即(2a-r)2+a2=r2 4a2-4ar+r2+a2=r2 5a2=4ar 5a=4r ∴r =a. B N E 方法二:如图,连结BD、OE、BE、DE. ∵四边形BCMN为正方形 ∴∠C=∠M=∠N=90° ∴BD为⊙O的直径,∠BED=90° M D ∴∠BEN+∠DEM =90° C ∵∠BEN+∠EBN=90° ∴∠DEM=∠EBN ∴△BNE∽△EMD ∴∴DM=a 由OE是梯形BDMN的中位线得OE=(BN+MD)=a. (4)①当a<r<时,⊙O与正方形的公共点个数可能有0、1、2、4、6、7、8个; ②当r=a时,⊙O与正方形的公共点个数可能有0、1、2、5、8个; ③当时,⊙O与正方形的公共点个数可能有0、1、2、3、4、6、8个; ④当时,⊙O与正方形的公共点个数可能有0、1、2、3、4个; ⑤当时,⊙O与正方形的公共点个数可能有0、1、2、3、4个. [点评]本题是一道较为新颖的几何压轴题,考查圆、相似、正方形等几何知识,综合性较强,有一定的难度,试题的区分度把握非常得当,是一道很不错的压轴题。 9. (06山东枣庄课改卷)半径为2.5的⊙O中,直径AB的不同侧有定点C和动点P.已知BC :CA=4 : 3,点P在上运动,过点C作CP的垂线,与PB的延长线交于点O (1)当点P与点C关于AB对称时,求CQ的长; (2)当点P运动到的中点时,求CQ的长; (3)当点P运动到什么位置时,CQ取到最大值?求此时CQ的长. [解] (1)当点P与点C关于AB对称时,CP⊥AB,设垂足为D. ∵AB为⊙O的直径,∴∠ACB=900. ∴AB=5,AC:CA=4:3,∴BC=4, AC=3. 又∵AC·BC=AB·CD ∴ 在Rt△ACB和Rt△PCQ中, ∠ACB=∠PCQ=900, ∠CAB=∠CPQ, Rt△ACB∽Rt△PCQ ∴ (2)当点P运动到弧AB的中点时,过点B作BE⊥PC 于点E(如图).∵P是弧AB的中点,∴ 又∠CPB=∠CAB∴∠CPB= tan∠CAB= ∴而从 由(l)得, (3)点P在弧AB上运动时,恒有 故PC最大时,CQ取到最大值. 当PC过圆心O,即PC取最大值5时,CQ 最大值为 [点评]本题属于常规的几何综合题,解第3小问时要有动态的思想(在草稿上画画图)不难猜想出结论。 10.如图,点在轴上,交轴于两点,连结并延长交于,过点的直线交轴于,且的半径为,. (1)求点的坐标; (2)求证:是的切线; D A C PC BC OC (3)若二次函数的图象经过点,求这个二次函数的解析式,并写出使二次函数值小于一次函数值的的取值范围. [解] (1)如图,连结 , 是的直径(也可用勾股定理求得下面的结论) , ,, (2)过点 当时, D A C PC BC OC , (也可用勾股定理逆定理证明) 是的切线 (3)过点 因为函数与的图象交点是和点(画图可得此结论) 所以满足条件的的取值范围是或 11. 如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O上一动点,且P在第一象限内,过点P作⊙O的切线与轴相交于点A,与轴相交于点B。 (1)点P在运动时,线段AB的长度在发生变化,请写出线段AB长度的最小值,并说明理由; (2)在⊙O上是否存在一点Q,使得以Q、O、A、P为顶点的四边形时平行四边形?若存在,请求出Q点的坐标;若不存在,请说明理由。 [解] (1)线段AB长度的最小值为4 理由如下:连接OP 因为AB切⊙O于P,所以OP⊥AB 取AB的中点C,则 当时,OC最短, 即AB最短,此时 (2)设存在符合条件的点Q, 如图①,设四边形APOQ为平行四边形, 因为四边形APOQ为矩形又因为所以四边形APOQ为正方形 所以, 在Rt△OQA中,根据,得Q点坐标为()。 如图②,设四边形APQO为平行四边形因为OQ∥PA,,所以,又因为所以, 因为 PQ∥OA,所以 轴。设轴于点H, 在Rt△OHQ中,根据,得Q点坐标为() 所以符合条件的点Q的坐标为()或()。 12. 如图①,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为,直线l: 与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M。 (1)求点A的坐标及∠CAO的度数; (2)⊙B以每秒1各单位长度的速度沿x轴负方向平移,同时,直线l绕点A顺时针匀速旋转。当⊙B第一次与⊙O相切时,直线l也恰好与⊙B第一次相切。问:直线AC绕点A每秒旋转多少度? A B O M C y x 第25题图① A E O C y x 第25题图② O1 (3)如图②,过A、O、C三点作⊙O1,点E为劣弧AO上一点,连接EC、EA、EO,当点E在劣弧AO上运动时(不与A、O两点重合),的值是否发生变化?如果不变,求其值;如果变化,说明理由。 13. (06广东深圳课改卷)(10分)如图10-1,在平面直角坐标系中,点在轴的正半轴上, ⊙交轴于 两点,交轴于两点,且为的中点,交轴于点,若点的坐标为(-2,0), (1)(3分)求点的坐标. (2)(3分)连结,求证:∥ (3)(4分) 如图10-2,过点作⊙的切线,交轴于点.动点在⊙的圆周上运动时,的比值是否发生变化,若不变,求出比值;若变化,说明变化规律. 14.(06 安徽芜湖市课改卷)一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与C D是水平的,BC与水平面的夹角为600,其中AB=60cm,CD=40cm,BC=40cm,请你作出该小朋友将园盘从A点滚动到D点其圆心所经过的路线的示意图,并求出此路线的长度。 15. (07芜湖市)24. 已知圆P的圆心在反比例函数图象上,并与x轴相交于A、B两点. 且始终与y轴相切于定点C(0,1). (1) 求经过A、B、C三点的二次函数图象的解析式; (2) 若二次函数图象的顶点为D,问当k为何值时,四边形ADBP为菱形. 解: (1)连结PC、PA、PB,过P点作PH⊥x轴,垂足为H. ∵⊙P与轴相切于点C (0,1),∴PC⊥轴. ∵P点在反比例函数的图象上, ∴P点坐标为(k,1). ∴PA=PC=k. 在Rt△APH中,AH==, ∴OA=OH—AH=k-. ∴A(k-,0). ∵由⊙P交x轴于A、B两点,且PH⊥AB,由垂径定理可知, PH垂直平分AB. ∴OB=OA+2AH= k-+2=k+,∴B(k+,0). 故过A、B两点的抛物线的对称轴为PH所在的直线解析式为x=k. 可设该抛物线解析式为y=a+h. 又抛物线过C(0,1), B(k+,0), 得: 解得a=1,h=1-. ∴抛物线解析式为y=+1-. (2)由(1)知抛物线顶点D坐标为(k, 1-)∴DH=-1. 若四边形ADBP为菱形.则必有PH=DH .∵PH=1,∴-1=1. 又∵k>1,∴k= ∴当k取时,PD与AB互相垂直平分,则四边形ADBP为菱形. 16. 26. 如图①,②,在平面直角坐标系中,点的坐标为(4,0),以点为圆心,4为半径的圆与轴交于,两点,为弦,,是轴上的一动点,连结. (1)求的度数;(2分)(2)如图①,当与相切时,求的长;(3分) (3)如图②,当点在直径上时,的延长线与相交于点,问为何值时,是等腰三角形?) 解:(1)∵,,∴是等边三角形. ∴. (2)∵CP与相切,∴. ∴. 又∵(4,0),∴.∴. ∴. (3)①过点作,垂足为,延长交于, ∵是半径, ∴,∴,∴是等腰三角形. 又∵是等边三角形,∴=2 . ②解法一:过作,垂足为,延长交于,与轴交于, ∵是圆心, ∴是的垂直平分线. ∴.∴是等腰三角形, 过点作轴于,在中,∵, ∴.∴点的坐标(4+,). 在中,∵,∴.∴点坐标(2,). 设直线的关系式为:,则有 解得:∴.当时,.∴. 解法二: 过A作,垂足为,延长交于,与轴交于, ∵是圆心, ∴是的垂直平分线. ∴.∴是等腰三角形. ∵,∴.∵平分,∴. ∵是等边三角形,, ∴. ∴. ∴是等腰直角三角形.∴.∴. 17. 26. 如图12-1所示,在中,,,为的中点,动点在边上自由移动,动点在边上自由移动. (1)点的移动过程中,是否能成为的等腰三角形?若能,请指出为等腰三角形时动点的位置.若不能,请说明理由. (2)当时,设,,求与之间的函数解析式,写出的取值范围. (3)在满足(2)中的条件时,若以为圆心的圆与相切(如图12-2),试探究直线与的位置关系,并证明你的结论. 图12-1 图12-2 A E F O C B A E F O C B (图12-1) (图12-2) 解:如图, (1)点移动的过程中,能成为的等腰三角形.此时点的位置分别是: ①是的中点,与重合. ②.③与重合,是的中点 (2)在和中,,, .又,.. ,,,. (3)与相切.,..即. 又,..点到和的距离相等. 与相切,点到的距离等于的半径.与相切. 18. (06武汉市) 如图①,在平面直角坐标系中,Rt△AOB≌Rt△CDA,且A(-1,0)、B(0,2),抛物线y=ax2+ax-2经过点C。(1)求抛物线的解析式; (2)在抛物线(对称轴的右侧)上是否存在两点P、Q,使四边形ABPQ是正方形?若存在,求点P、Q的坐标,若不存在,请说明理由; (3)如图②,E为BC延长线上一动点,过A、B、E三点作⊙O’,连结AE,在⊙O’上另有一点F,且AF=AE,AF交BC于点G,连结BF。下列结论:①BE+BF的值不变;②,其中有且只有一个成立,请你判断哪一个结论成立,并证明成立的结论。 O x y B F A E C O’ G (第25题图②) O (第25题图①) A B C D x y 解:⑴由Rt△AOB≌Rt△CDA得OD=2+1=3,CD=1∴C点坐标为(-3,1), ∵抛物线经过点C,∴1= (-3)2 a+(-3)a-2,∴。∴抛物线的解析式为. ⑵在抛物线(对称轴的右侧)上存在点P、Q,使四边形ABPQ是正方形。 以AB边在AB右侧作正方形ABPQ。过P作PE⊥OB于E,QG⊥x轴于G,可证△PBE≌△AQG≌△BAO, ∴PE=AG=BO=2,BE=QG=AO=1,∴∴P点坐标为(2,1),Q点坐标为(1,-1)。 由(1)抛物线。当x=2时,y=1,当x=,1时,y=-1。∴P、Q在抛物线上。 故在抛物线(对称轴的右侧)上存在点P(2,1)、Q(1,-1),使四边形ABPQ是正方形。 ⑵另解:在抛物线(对称轴的右侧)上存在点P、Q,使四边形ABPQ是正方形。 延长CA交抛物线于Q,过B作BP∥CA交抛物线于P,连PQ,设直线CA、BP的解析式分别为y=k1x+b1, y=k2x+b2, ∵A(-1,0),C(-3,1),∴CA的解析式,同理BP的解析式为, 解方程组得Q点坐标为(1,-1),同理得P点坐标为(2,1)。 由勾股定理得AQ=BP=AB=,而∠BAQ=90°, ∴四边形ABPQ是正方形。故在抛物线(对称轴的右侧)上存在点P(2,1)、Q(1,-1),使四边形ABPQ是正方形。 ⑵另解:在抛物线(对称轴的右侧)上存在点P、Q,使四边形ABPQ是正方形。如图,将线段CA沿CA方向平移至AQ,∵C(-3,1)的对应点是A(-1,0),∴A(-1,0)的对应点是Q(1,-1),再将线段AQ沿AB方向平移至BP,同理可得P(2,1) ∵∠BAC=90°,AB=AC ∴四边形ABPQ是正方形。经验证P(2,1)、Q(1,-1)两点均在抛物线上。 ⑶结论②成立, 证明如下:连EF,过F作FM∥BG交AB的延长线于M,则△AMF∽△ABG,∴。 由⑴知△ABC是等腰直角三角形,∴∠1=∠2=45°。∵AF=AE,∴∠AEF=∠1=45°。 ∴∠EAF=90°,EF是⊙O´的直径。∴∠EBF=90°。∵FM∥BG, ∴∠MFB=∠EBF=90°,∠M=∠2=45°,∴BF=MF,∴ 24、如图12,形如三角板的∆ABC中,∠ACB=90°,∠ABC=45°,BC=12cm,形如矩形量角器的半圆O的直径DE=12cm,矩形DEFG的宽EF=6cm,矩形量角器以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在BC所在的直线上,设运动时间为x(s),矩形量角器和∆ABC的重叠部分的面积为S(cm2).当x=0(s)时,点E与点C重合.(图(3)、图(4)、图(5)供操作用). (1)当x=3时,如图(2),S= cm2, 当x=6时,S= cm2, 当x=9时,S= cm2; (2)当3查看更多