- 2021-06-26 发布 |
- 37.5 KB |
- 4页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北京课改版数学八上《直角三角形》练习题
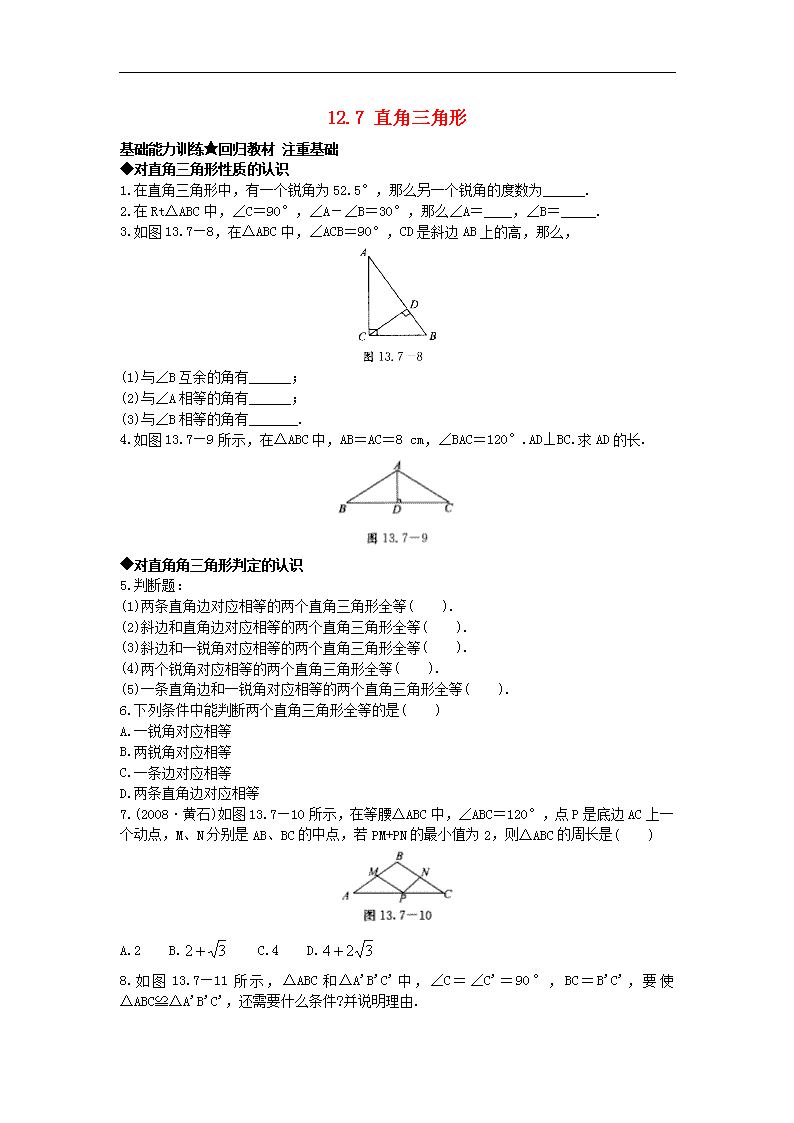
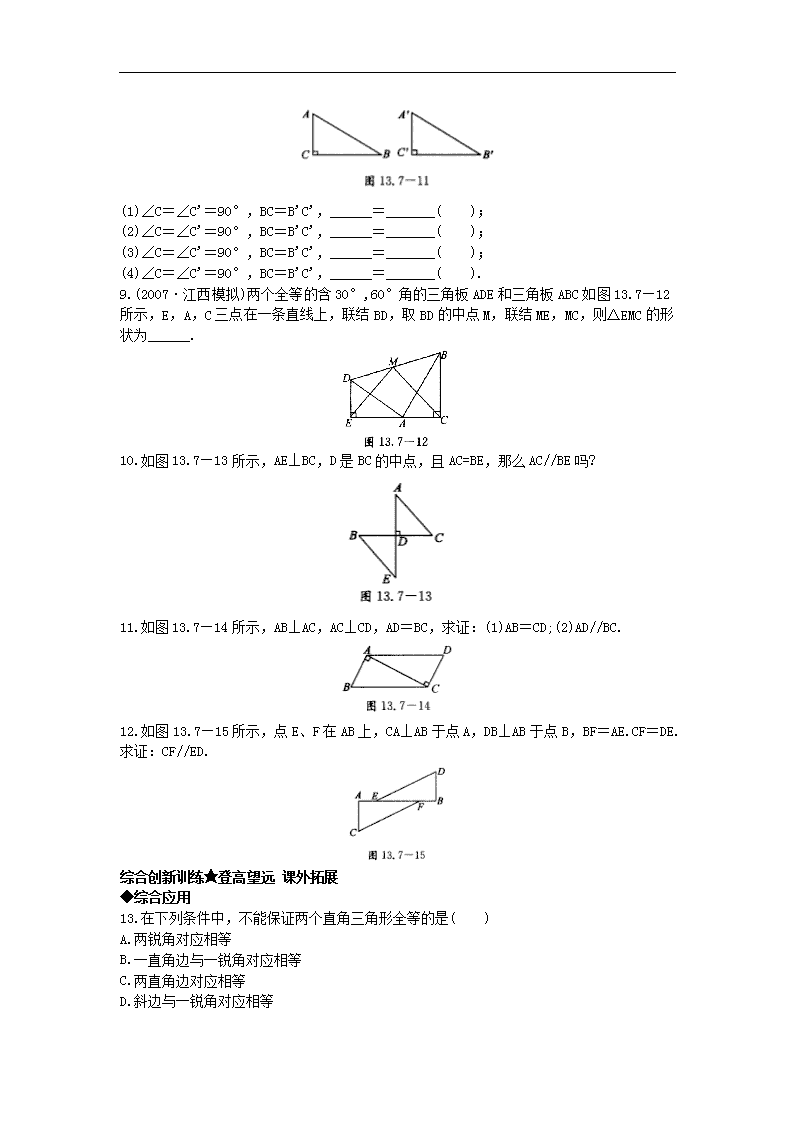
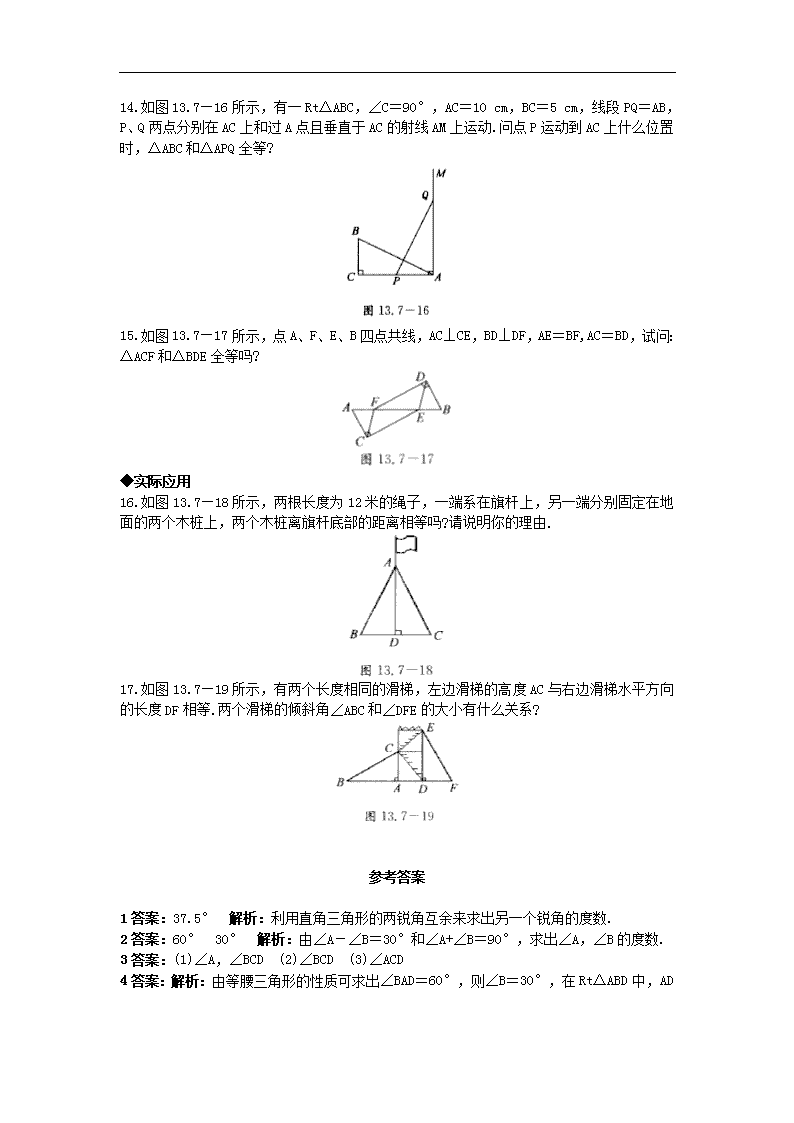
12.7 直角三角形 基础能力训练★回归教材 注重基础 ◆对直角三角形性质的认识 1.在直角三角形中,有一个锐角为 52.5°,那么另一个锐角的度数为______. 2.在 Rt△ABC 中,∠C=90°,∠A-∠B=30°,那么∠A=____,∠B=_____. 3.如图 13.7—8,在△ABC 中,∠ACB=90°,CD 是斜边 AB 上的高,那么, (1)与∠B 互余的角有______; (2)与∠A 相等的角有______; (3)与∠B 相等的角有_______. 4.如图 13.7—9 所示,在△ABC 中,AB=AC=8 cm,∠BAC=120°.AD⊥BC.求 AD 的长. ◆对直角角三角形判定的认识 5.判断题: (1)两条直角边对应相等的两个直角三角形全等( ). (2)斜边和直角边对应相等的两个直角三角形全等( ). (3)斜边和一锐角对应相等的两个直角三角形全等( ). (4)两个锐角对应相等的两个直角三角形全等( ). (5)一条直角边和一锐角对应相等的两个直角三角形全等( ). 6.下列条件中能判断两个直角三角形全等的是( ) A.一锐角对应相等 B.两锐角对应相等 C.一条边对应相等 D.两条直角边对应相等 7.(2008·黄石)如图 13.7—10 所示,在等腰△ABC 中,∠ABC=120°,点 P 是底边 AC 上一 个动点,M、N 分别是 AB、BC 的中点,若 PM+PN 的最小值为 2,则△ABC 的周长是( ) A.2 B. 32 C.4 D. 324 8.如图 13.7— 11 所示 ,△ABC 和△A'B'C'中, ∠C=∠C'= 90°, BC=B'C',要 使 △ABC≌△A'B'C',还需要什么条件?并说明理由. (1)∠C=∠C'=90°,BC=B'C',______=_______( ); (2)∠C=∠C'=90°,BC=B'C',______=_______( ); (3)∠C=∠C'=90°,BC=B'C',______=_______( ); (4)∠C=∠C'=90°,BC=B'C',______=_______( ). 9.(2007·江西模拟)两个全等的含 30°,60°角的三角板 ADE 和三角板 ABC 如图 13.7—12 所示,E,A,C 三点在一条直线上,联结 BD,取 BD 的中点 M,联结 ME,MC,则△EMC 的形 状为______. 10.如图 13.7—13 所示,AE⊥BC,D 是 BC 的中点,且 AC=BE,那么 AC//BE 吗? 11.如图 13.7—14 所示,AB⊥AC,AC⊥CD,AD=BC,求证:(1)AB=CD;(2)AD//BC. 12.如图 13.7—15 所示,点 E、F 在 AB 上,CA⊥AB 于点 A,DB⊥AB 于点 B,BF=AE.CF=DE. 求证:CF//ED. 综合创新训练★登高望远 课外拓展 ◆综合应用 13.在下列条件中,不能保证两个直角三角形全等的是( ) A.两锐角对应相等 B.一直角边与一锐角对应相等 C.两直角边对应相等 D.斜边与一锐角对应相等 14.如图 13.7—16 所示,有一 Rt△ABC,∠C=90°,AC=10 cm,BC=5 cm,线段 PQ=AB, P、Q 两点分别在 AC 上和过 A 点且垂直于 AC 的射线 AM 上运动.问点 P 运动到 AC 上什么位置 时,△ABC 和△APQ 全等? 15.如图 13.7—17 所示,点 A、F、E、B 四点共线,AC⊥CE,BD⊥DF,AE=BF,AC=BD,试问: △ACF 和△BDE 全等吗? ◆实际应用 16.如图 13.7—18 所示,两根长度为 12 米的绳子,一端系在旗杆上,另一端分别固定在地 面的两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由. 17.如图 13.7—19 所示,有两个长度相同的滑梯,左边滑梯的高度 AC 与右边滑梯水平方向 的长度 DF 相等.两个滑梯的倾斜角∠ABC 和∠DFE 的大小有什么关系? 参考答案 1 答案:37.5° 解析:利用直角三角形的两锐角互余来求出另一个锐角的度数. 2 答案:60° 30° 解析:由∠A-∠B=30°和∠A+∠B=90°,求出∠A,∠B 的度数. 3 答案:(1)∠A,∠BCD (2)∠BCD (3)∠ACD 4 答案:解析:由等腰三角形的性质可求出∠BAD=60°,则∠B=30°,在 Rt△ABD 中,AD = 2 1 AB=4(cm). 5 答案:(1)正确;(2)正确;(3)正确;(4)错误;(5)正确. 6 答案:D 解析:利用 SAS 来说明全等 7 答案:D 解析:当 PM+PN 最小时,P 为 AC 的中点,所以可知 BA+BC=4,且 BA=BC=2, 又因为∠ABC=120°,所以∠A=30°,所以 AC 边上的高为 1,从而可求得 32AC . 8 答案:(1)AC A'C' SAS (2)∠A ∠A' AAS (3)AB A'B' HL (4)∠B ∠B' ASA 9 答案:等腰直角三角形 10 答案:解析:AC∥BE, ∵D 是 BC 的中点,∴DB=DC,∵AE⊥BC,且 AC=BE, ∴Rt△ADC≌Rt△EDB(HL),∴∠B=∠C,∴AC∥BE. 11 答案:证明:(1)∵AD=BC(已知),AC=CA(公共边),∴Rt△ABC≌Rt△CDA(HL),∴AB= CD; (2)∵Rt△ABC≌Rt△CDA,∴∠BCA=∠DAC, ∴AD∥BC. 12 答案:证明:∵CA⊥AB 于点 A,DB 上 AB 于点 B,∴∠A=∠B=90°, ∵BF=AE,∴AF=BE,∵CF=DE. ∴△AFC≌△BED(HL),∴∠AFC=∠BED.∴CF∥ED. 13 答案:A 解析:两个锐角对应相等的两个直角三角形不全等. 14 答案:解析:由题意可知,∠C=∠PAQ=90°.要△ABC 和△APQ 全等,只需 PA=BC 或 AP =AC 即可,从而当点 P 运动到 AP=5 cm,即 AC 的中点时,△ABC≌△QPA.或 P 点与 C 点重 合时,△ABC≌△PQA. 15 答案:解析:∵AC⊥CE,BD⊥DF,∴∠ACE=∠BDF=90°, ∵在 Rt△ACE 和 Rt△BDF 中,AE=BF,AC=BD, ∴Rt△ACE≌Rt△BDF,∴∠A=∠B, ∵AE=BF,∴AF=BE, ∴△ACF≌△BDE(SAS). 16 答案:解析:∵AD⊥BC,∴∠ADB=∠ADC=90°, ∵AB=AC,∴Rt△ADB≌Rt△ADC, ∴DB=DC,即两个木桩离旗杆底部的距离相等. 17 答案:解析:∠ABC 和∠DFE 互余, ∵BC=EF,AC=DF,∴Rt△ABC≌Rt△DEF(HL), ∴∠ABC=∠DEF,∵∠DEF+∠DFE=90°, ∴∠ABC+∠DFE=90°.即∠ABC 和∠DFE 互余.查看更多