- 2021-02-26 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年湖北省恩施州中考数学试卷【含答案;word版本试题;可编辑】
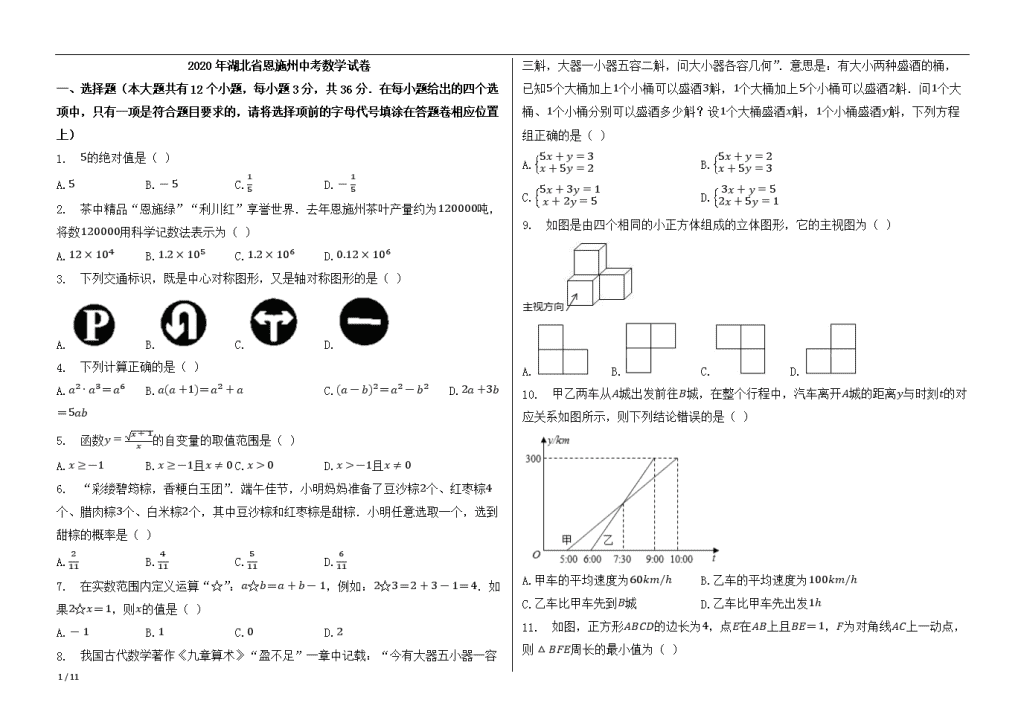
2020年湖北省恩施州中考数学试卷 一、选择题(本大题共有12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将选择项前的字母代号填涂在答题卷相应位置上) 1. 5的绝对值是( ) A.5 B.-5 C.15 D.-15 2. 茶中精品“恩施绿”“利川红”享誉世界.去年恩施州茶叶产量约为120000吨,将数120000用科学记数法表示为( ) A.12×104 B.1.2×105 C.1.2×106 D.0.12×106 3. 下列交通标识,既是中心对称图形,又是轴对称图形的是( ) A. B. C. D. 4. 下列计算正确的是( ) A.a2⋅a3=a6 B.a(a+1)=a2+a C.(a-b)2=a2-b2 D.2a+3b=5ab 5. 函数y=x+1x的自变量的取值范围是( ) A.x≥-1 B.x≥-1且x≠0 C.x>0 D.x>-1且x≠0 6. “彩缕碧筠粽,香粳白玉团”.端午佳节,小明妈妈准备了豆沙粽2个、红枣粽4个、腊肉粽3个、白米粽2个,其中豆沙粽和红枣粽是甜粽.小明任意选取一个,选到甜粽的概率是( ) A.211 B.411 C.511 D.611 7. 在实数范围内定义运算“☆”:a☆b=a+b-1,例如:2☆3=2+3-1=4.如果2☆x=1,则x的值是( ) A.-1 B.1 C.0 D.2 8. 我国古代数学著作《九章算术》“盈不足”一章中记载:“今有大器五小器一容三斛,大器一小器五容二斛,问大小器各容几何”.意思是:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛.问1个大桶、1个小桶分别可以盛酒多少斛?设1个大桶盛酒x斛,1个小桶盛酒y斛,下列方程组正确的是( ) A.5x+y=3x+5y=2 B.5x+y=2x+5y=3 C.5x+3y=1x+2y=5 D.3x+y=52x+5y=1 9. 如图是由四个相同的小正方体组成的立体图形,它的主视图为( ) A. B. C. D. 10. 甲乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是( ) A.甲车的平均速度为60km/h B.乙车的平均速度为100km/h C.乙车比甲车先到B城 D.乙车比甲车先出发1h 11. 如图,正方形ABCD的边长为4,点E在AB上且BE=1,F为对角线AC上一动点, 11 / 11 则△BFE周长的最小值为( ) A.5 B.6 C.7 D.8 12. 如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(-2, 0)、B(1, 0)两点.则以下结论:①ac>0;②二次函数y=ax2+bx+c的图象的对称轴为x=-1;③2a+c=0;④a-b+c>0.其中正确的有( )个. A.0 B.1 C.2 D.3 二、填空题(本大题共有4小题,每小题3分,共12分.不要求写出解答过程,请把答案直接填写在答题卷相应位置上) 13. 9的算术平方根是________. 14. 如图,直线l1 // l2,点A在直线l1上,点B在直线l2上,AB=BC,∠C=30∘,∠1=80∘,则∠2=________. 15. 如图,已知半圆的直径AB=4,点C在半圆上,以点A为圆心,AC为半径画弧交AB于点D,连接BC.若∠ABC=60∘,则图中阴影部分的面积为________.(结果不取近似值 16. 如图,在平面直角坐标系中,△ABC的顶点坐标分别为:A(-2, 0),B(1, 2),C(1, -2).已知N(-1, 0),作点N关于点A的对称点N1,点N1关于点B的对称点N2,点N2关于点C的对称点N3,点N3关于点A的对称点N4,点N4关于点B的对称点N5,…,依此类推,则点N2020的坐标为________. 三、解答题(本大题共有8个小题,共72分.请在答题卷指定区域内作答,解答时应写出文字说明、证明过程或演算步骤). 17. 先化简,再求值:(m2-9m2-6m+9-3m-3)÷m2m-3,其中m=2. 11 / 11 18. 如图,AE // BF,BD平分∠ABC交AE于点D,点C在BF上且BC=AB,连接CD.求证:四边形ABCD是菱形. 19. 某中学为了解九年级学生对XXXXXXXXXX知识的掌握情况,从全校九年级学生中随机抽取部分学生进行调查.调查结果分为四类:A类--非常了解;B类--比较了解;C类--般了解;D类--不了解.现将调查结果绘制成如图不完整的统计图,请根据统计图中的信息解答下列问题: (1)本次共调查了________名学生; (2)补全条形统计图; (3)D类所对应扇形的圆心角的大小为________; (4)若该校九年级学生共有500名,根据以上抽样结果,估计该校九年级学生对XXXXXXXXXX知识非常了解的约有________名. 11 / 11 20. 如图,一艘轮船以每小时30海里的速度自东向西航行,在A处测得小岛P位于其西北方向(北偏西45∘方向),2小时后轮船到达B处,在B处测得小岛P位于其北偏东60∘方向.求此时船与小岛P的距离(结果保留整数,参考数据:2≈1.414,3≈1.732). 21. 如图,在平面直角坐标系中,直线y=ax-3a(a≠0)与x轴、y轴分别相交于A、B两点,与双曲线y=kx(x>0)的一个交点为C,且BC=12AC. (1)求点A的坐标; (2)当S△AOC=3时,求a和k的值. 22. 某校足球队需购买A、B两种品牌的足球.已知A品牌足球的单价比B品牌足球的单价高20元,且用900元购买A品牌足球的数量用720元购买B品牌足球的数量相等. (1)求A、B两种品牌足球的单价; (2)若足球队计划购买A、B两种品牌的足球共90个,且A品牌足球的数量不小于B品牌足球数量的2倍,购买两种品牌足球的总费用不超过8500元.设购买A品牌足球m个,总费用为W元,则该队共有几种购买方案?采用哪一种购买方案可使总费用最低?最低费用是多少元? 11 / 11 23. 如图1,AB是⊙O的直径,直线AM与⊙O相切于点A,直线BN与⊙O相切于点B,点C(异于点A)在AM上,点D在⊙O上,且CD=CA,延长CD与BN相交于点E,连接AD并延长交BN于点F. (1)求证:CE是⊙O的切线; (2)求证:BE=EF; (3)如图2,连接EO并延长与⊙O分别相交于点G、H,连接BH.若AB=6,AC=4,求tan∠BHE. 24. 如图1,抛物线y=-14x2+bx+c经过点C(6, 0),顶点为B,对称轴x=2与x轴相交于点A,D为线段BC的中点. 11 / 11 (1)求抛物线的解析式; (2)P为线段BC上任意一点,M为x轴上一动点,连接MP,以点M为中心,将△MPC逆时针旋转90∘,记点P的对应点为E,点C的对应点为F.当直线EF与抛物线y=-14x2+bx+c只有一个交点时,求点M的坐标. (3)△MPC在(2)的旋转变换下,若PC=2(如图2). ①求证:EA=ED. ②当点E在(1)所求的抛物线上时,求线段CM的长. 11 / 11 参考答案与试题解析 2020年湖北省恩施州中考数学试卷 一、选择题(本大题共有12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将选择项前的字母代号填涂在答题卷相应位置上) 1.A 2.B 3.D 4.B 5.B 6.D 7.C 8.A 9.A 10.D 11.B 12.C 二、填空题(本大题共有4小题,每小题3分,共12分.不要求写出解答过程,请把答案直接填写在答题卷相应位置上) 13.3 14.40∘ 15.23-π 16.(-1, 8) 三、解答题(本大题共有8个小题,共72分.请在答题卷指定区域内作答,解答时应写出文字说明、证明过程或演算步骤). 17.(m2-9m2-6m+9-3m-3)÷m2m-3 =[(m+3)(m-3)(m-3)2-3m-3]⋅m-3m2 =(m+3m-3-3m-3)⋅m-3m2 =mm-3⋅m-3m2 =1m; 当m=2时, 原式=12=22. 18.证明:∵ AE // BF, ∴ ∠ADB=∠DBC, ∵ BD平分∠ABC, ∴ ∠DBC=∠ABD, ∴ ∠ADB=∠ABD, ∴ AB=AD, 又∵ AB=BC, ∴ AD=BC, ∵ AE // BF,即AD // BC, ∴ 四边形ABCD为平行四边形, 又∵ AB=AD, ∴ 四边形ABCD为菱形. 19.50 C类学生人数为:50-15-20-5=10(名), 条形图如下: 11 / 11 36∘ 150 20.此时船与小岛P的距离约为44海里. 21.(3, 0) a=-1,k=2 22.购买A品牌足球的单价为100元,则购买B品牌足球的单价为80元; 该队共有6种购买方案,购买60个A品牌30个B品牌的总费用最低,最低费用是8400元 23.如图1中,连接OD, ∵ CD=CA, ∴ ∠CAD=∠CDA, ∵ OA=OD ∴ ∠OAD=∠ODA, ∵ 直线AM与⊙O相切于点A, ∴ ∠CAO=∠CAD+∠OAD=90∘, ∴ ∠ODC=∠CDA+∠ODA=90∘, ∴ CE是⊙O的切线. 如图2中,连接BD, ∵ OD=OB, ∴ ∠ODB=∠OBD, ∵ CE是⊙O的切线,BF是⊙O的切线, ∴ ∠OBD=∠ODE=90∘, ∴ ∠EDB=∠EBD, ∴ ED=EB, ∵ AM⊥AB,BN⊥AB, ∴ AM // BN, ∴ ∠CAD=∠BFD, ∵ ∠CAD=∠CDA=∠EDF, ∴ ∠BFD=∠EDF, ∴ EF=ED, ∴ BE=EF. 如图2中,过E点作EL⊥AM于L,则四边形ABEL是矩形, 设BE=x,则CL=4-x,CE=4+x, ∴ (4+x)2=(4-x)2+62, 解得:x=94, ∴ tan∠BOE=BEOB=943=34, ∵ ∠BOE=2∠BHE, 11 / 11 ∴ tan∠BOE=2tan∠BHE1-tan2∠BHE=34, 解得:tan∠BHE=13或-3(-3不合题意舍去), ∴ tan∠BHE=13. 补充方法:如图2中,作HJ⊥EB交EB的延长线于J. ∵ tab∠BOE=BEOB=34, ∴ 可以假设BE=3k,OB=4k,则OE=5k, ∵ OB // HJ, ∴ OBHJ=OEEH=EBEJ, ∴ 4kHJ=5k9k=3kEJ, ∴ HJ=365k,EJ=275k, ∴ BJ=EJ-BE=275k-3k=125k ∴ tan∠BHJ=BJHJ=13, ∵ ∠BHE=∠OBE=∠BHJ, ∴ tan∠BHE=13. 24.∵ 点C(6, 0)在抛物线上, ∴ 0=-14×36+6b+c, 得到6b+c=9, 又∵ 对称轴x=2, ∴ x=-b2a=-b2×(-14)=2, 解得b=1, ∴ c=3, ∴ 二次函数的解析式为y=-14x2+x+3; 当点M在点C的左侧时,如图2-1中: ∵ 抛物线的解析式为y=-14x2+x+3,对称轴为x=2,C(6, 0) ∴ 点A(2, 0),顶点B(2, 4), ∴ AB=AC=4, ∴ △ABC是等腰直角三角形, ∴ ∠1=45∘; ∵ 将△MPC逆时针旋转90∘得到△MEF, ∴ FM=CM,∠2=∠1=45∘, 设点M的坐标为(m, 0), ∴ 点F(m, 6-m), 又∵ ∠2=45∘, ∴ 直线EF与x轴的夹角为45∘, ∴ 设直线EF的解析式为y=x+b, 11 / 11 把点F(m, 6-m)代入得:6-m=m+b,解得:b=6-2m, 直线EF的解析式为y=x+6-2m, ∵ 直线EF与抛物线y=-14x2+x+3只有一个交点, ∴ y=x+6-2my=-14x2+x+3 , 整理得:14x2+3-2m=0, ∴ △=b2-4ac=0,解得m=32, 点M的坐标为(32, 0). 当点M在点C的右侧时,如下图: 由图可知,直线EF与x轴的夹角仍是45∘,因此直线EF与抛物线y=-14x2+x+3不可能只有一个交点. 综上,点M的坐标为(32, 0). ①当点M在点C的左侧时,如下图,过点P作PG⊥x轴于点G,过点E作EH⊥x轴于点H, ∵ PC=2,由(2)知∠BCA=45∘, ∴ PG=GC=1, ∴ 点G(5, 0), 设点M的坐标为(m, 0), ∵ 将△MPC逆时针旋转90∘得到△MEF, ∴ EM=PM, ∵ ∠HEM+∠EMH=∠GMP+∠EMH=90∘, ∴ ∠HEM=∠GMP, 在△EHM和△MGP中,∠EHM=∠MGP∠HEM=∠GMPEM=MP , ∴ △EHM≅△MGP(AAS), ∴ EH=MG=5-m,HM=PG=1, ∴ 点H(m-1, 0), ∴ 点E的坐标为(m-1, 5-m); ∴ EA=(m-1-2)2+(5-m-0)2=2m2-16m+34, 又∵ D为线段BC的中点,B(2, 4),C(6, 0), ∴ 点D(4, 2), ∴ ED=(m-1-4)2+(5-m-2)2=2m2-16m+34, 11 / 11 ∴ EA=ED. 当点M在点C的右侧时,如下图: 同理,点E的坐标仍为(m-1, 5-m),因此EA=ED. ②当点E在(1)所求的抛物线y=-14x2+x+3上时, 把E(m-1, 5-m)代入,整理得:m2-10m+13=0, 解得:m=5+23或m=5-23, ∴ CM=23-1或CM=1+23. 11 / 11查看更多