- 2021-06-23 发布 |
- 37.5 KB |
- 4页


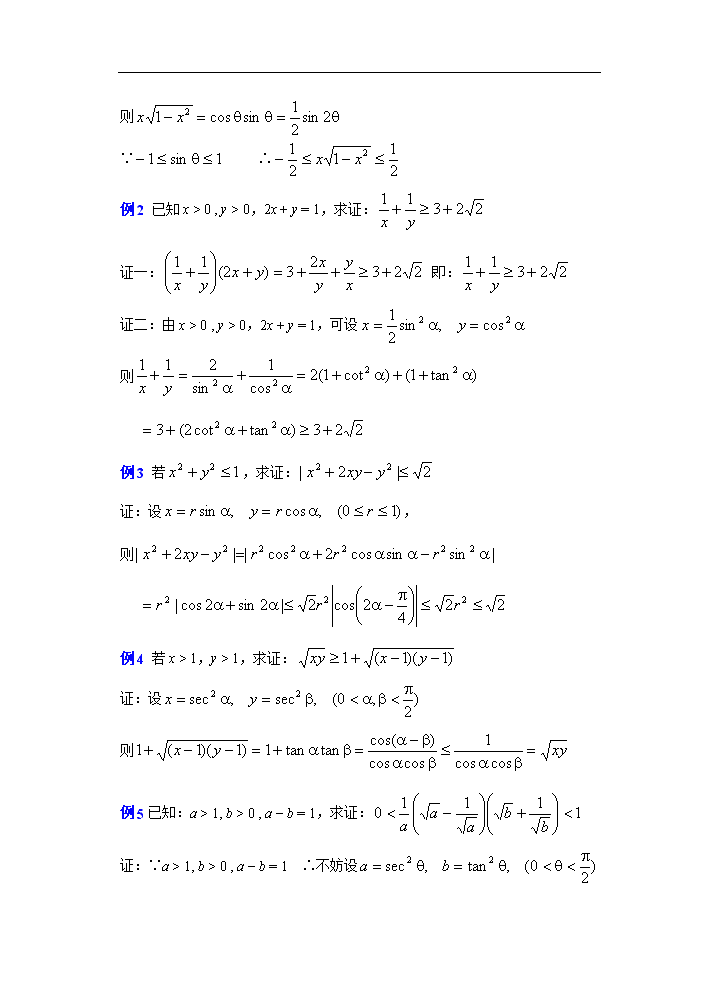
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学第6章(第9课时)不等式的证明(4)
课 题:不等式的证明(4) 教学目的: 1. 掌握换元法法证明不等式; 2.理解换元法实质; 3.提高证明不等式证法灵活性 教学重点:三角换元和代数换元 教学难点: 三角换元 授课类型:新授课 课时安排:1课时 教 具:多媒体、实物投影仪 教学过程: 一、复习引入: 1.重要不等式: 如果 2.定理:如果a,b是正数,那么 3公式的等价变形:ab≤,ab≤()2 4. ≥2(ab>0),当且仅当a=b时取“=”号; 5.定理:如果,那么(当且仅当时取“=”) 6.推论:如果,那么 (当且仅当时取“=”) 7.比较法之一(作差法)步骤:作差——变形——判断与0的关系——结论 比较法之二(作商法)步骤:作商——变形——判断与1的关系——结论 8.综合法:利用某些已经证明过的不等式(例如算术平均数与几何平均数定理)和不等式的性质推导出所要证明的不等式成立,这种证明方法叫做综合法 用综合法证明不等式的逻辑关系是: 综合法的思维特点是:由因导果,即由已知条件出发,利用已知的数学定理、性质和公式,推出结论的一种证明方法 9分析法: 证明不等式时,有时可以从求证的不等式出发,分析使这个不等式成立的条件,把证明不等式转化为判定这些条件是否具备的问题,如果能够肯定这些条件都已具备,那么就可以断定原不等式成立,这种方法叫做分析法 用分析法证明不等式的逻辑关系是: 分析法的思维特点是:执果索因 分析法的书写格式: 要证明命题B为真, 只需要证明命题为真,从而有…… 这只需要证明命题为真,从而又有…… …… 这只需要证明命题A为真 而已知A为真,故命题B必为真 二、讲解新课: 1三角换元: 若0≤x≤1,则可令x = sinq ()或x = sin2q () 若,则可令x = cosq , y = sinq () 若,则可令x = secq, y = tanq () 若x≥1,则可令x = secq () 若xÎR,则可令x = tanq () 2代数换元: “整体换元”,“均值换元”,“设差换元”的方法 三、讲解范例: 例1 求证: 证一:(综合法) ∵ 即 ∴ 证二:(换元法) ∵ ∴令 x = cosq , qÎ[0, p] 则 ∵ ∴ 例2 已知x > 0 , y > 0,2x + y = 1,求证: 证一: 即: 证二:由x > 0 , y > 0,2x + y = 1,可设 则 例3 若,求证: 证:设, 则 例4 若x > 1,y > 1,求证: 证:设 则 例5已知:a > 1, b > 0 , a - b = 1,求证: 证:∵a > 1, b > 0 , a - b = 1 ∴不妨设 则 ∵, ∴0 < sinq < 1 ∴ 例6证明:若a > 0,则 证:设 则 ( 当a = 1时取“=” ) ∴ 即 ∴原式成立 四、课堂练习: 五、小结 : 六、课后作业: 七、板书设计(略) 八、课后记: 查看更多