- 2021-06-18 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修1教案:第四章(第33课时)复习与小结(1)
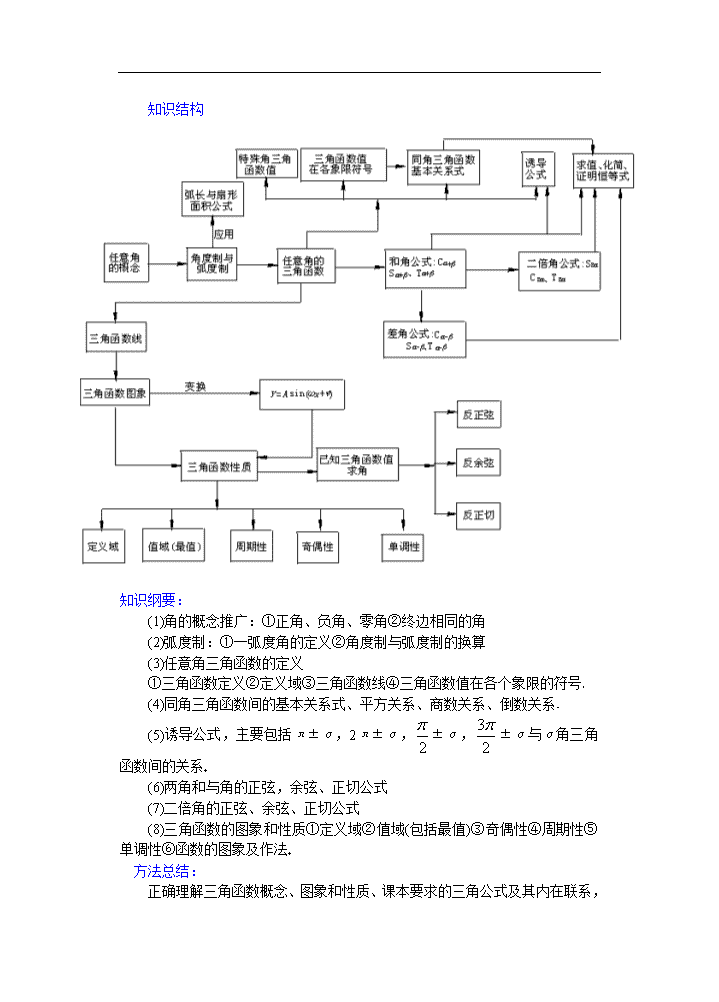
课 题:小结与复习(1) 知识目标: 1任意角的三角函数、任意角的概念、弧度制、任意角的三角函数的概念、同角三角函数间的关系、诱导公式; 2两角和与差的三角函数、二倍角的三角函数; 3三角函数的图象和性质、已知三角函数值求角 教学目的: 1理解任意角的概念、弧度的意义;能正确地进行弧度与角度的换算; 2掌握任意角的正弦、余弦、正切的定义,并会利用与单位圆有关的三角函数线表示正弦、余弦和正切;了解任意角的余切、正割、余割的定义;掌握同角三角函数的基本关系式;掌握正弦、余弦的诱导公式; 3掌握两角和与两角差的正弦、余弦、正切公式;掌握二倍角的正弦、余弦、正切公式; 4能正确运用三角公式,进行三角函数式的化简、求值及恒等式证明; 5会用与单位圆有关的三角函数线画出正弦函数、正切函数的图象,并在此基础上由诱导公式画出余弦函数的图象;理解周期函数与最小正周期的意义;并通过它们的图象理解正弦函数、余弦函数、正切函数的性质;会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+)的简图,理解A、ω、的物理意义; 6会用已知三角函数值求角,并会用符号arcsinx、arccosx、arctanx表示 教学重点:三角函数的知识网络结构及各部分知识 教学难点:熟练掌握各部分知识,并能灵活应用其解决相关问题 德育目标: 1渗透“变换”思想、“化归”思想; 2培养逻辑推理能力; 3培养学生探求精神 教学方法: 引导式 运用“整体化”教学思想,引导学生生从“整体”到“局部”再到“整体”逐步认识 授课类型:复习课 课时安排:1课时 教 具:多媒体、实物投影仪 教学过程: 一、本章知识与方法总结: 知识结构 知识纲要: (1)角的概念推广:①正角、负角、零角②终边相同的角 (2)弧度制:①一弧度角的定义②角度制与弧度制的换算 (3)任意角三角函数的定义 ①三角函数定义②定义域③三角函数线④三角函数值在各个象限的符号 (4)同角三角函数间的基本关系式、平方关系、商数关系、倒数关系 (5)诱导公式,主要包括π±α,2π±α,±α,±α与α角三角函数间的关系 (6)两角和与角的正弦,余弦、正切公式 (7)二倍角的正弦、余弦、正切公式 (8)三角函数的图象和性质①定义域②值域(包括最值)③奇偶性④周期性⑤单调性⑥函数的图象及作法 方法总结: 正确理解三角函数概念、图象和性质、课本要求的三角公式及其内在联系,是学习本章内容的基础。 1已知一个角的一个三角函数值,求这个角的其他三角函数值的方法; 2利用诱导公式求任意角三角函数值的方法; 3已知一个角的一个三角函数值,求符合条件的角的方法; 4利用三角公式进行恒等变形的方法(变角、变次数、变函数名称、变运算关系等) 5证明角相等的方法和证明三角恒等式的方法; 6作三角函数图象的方法; 7三角函数图象变换的方法; 8研究三角函数性质的方法 二、讲解新课: 这一章的知识网络结构: 最先,我们给出了三角函数的定义,包括任意角的三角函数的符号,同角三角函数的关系式,诱导公式,两角和与差的三角函数公式,以及它们的变形公式等等然后,我们又共同学习了三角函数(主要是:正弦函数、余弦函数、正切函数)的图象和性质接下来,我们又共同探讨了它们的应用运用上述公式和性质主要是进行三角函数式的化简、求值、证明以及它们的综合运用 具体内容: 根据生产实际和进一步学习数学的需要,我们引入了任意角的概念,并学习了角的另一种单位制——弧度制这里规定长度等于半径长的弧所对的圆心角叫做1弧度的角于是,弧长公式为:l=|α|r(其中l′为弧长,r为半径,α为圆弧所对圆心角的弧度数)之后,我们定义了任意角的正弦、余弦、正切、余切、正割、余割六种三角函数,它们都是以角为自变量,以此值为函数值的函数,其中,正弦、余弦、正切函数尤为重要,进而我们根据定义又得到了同角三角函数的基本关系式,它们是进行三角恒等变换的重要基础,而后,我们又得到了五组诱导公式 对于这部分知识,大家要理解任意角的概念、弧度的意义并能正确地进行弧度与角度的换算,掌握任意角的正弦、余弦、正切的定义,并学会利用与单位有关的三角函数线表示正弦、余弦和正切;另外需要了解任意角的余切、正割、余割的定义;还要掌握同角三角函数的基本关系式sin2α+cos2α=1,,tanαcotα=1,以及正弦、余弦诱导公式 和角公式、倍角公式、差角公式:利用单位圆和三角函数的定义,借助平面内任意两点之间的距离公式,我们最先得到了两角和的余弦公式,结合诱导公式,我们进而推导出两角和的正弦公式,利用同角三角函数基本关系式,可得到两角和的正切公式,之后用-β代替β,便可推得一组差角公式α与β相等时,便又可推出一组倍角公式看来,和角公式C(α+β) 是这些公式的基础,这些公式主要用于三角函数式的计算、化简与推导,它们在数学和许多其他学科中都有广泛的应用,希望大家能熟练掌握,并了解它们的内在联系 正弦、余弦、正切函数的图象以及它们的主要性质:利用平移正弦线,可以比较精确地画出正弦函数的图象;利用正弦函数的图象和诱导公式,可以画出余弦函数的图象,可以看出在长度为一个周期的闭区间上有五个点(即函数值最大和最小的点以及函数值为0的点)在确定正弦函数、余弦函数图象的形状时起着关键的作用因此,在精确度不太高时,我们常用“五点法”画正弦、余弦函数以及与它们类似的一些函数(特别是函数y=Asin(ωx+))的简图观察图象,可知它们的定义域、值域、周期性、奇偶性、单调性等,这部分知识,同学们要牢固掌握最后,关于三角函数的应用,还有已知三角函数值求角,并学会用arcsinx,arccosx,arctanx表示 在掌握这些知识之余,还应注意到这一章大量运用了化归思想,这是一种重要的数学思想,它主要表现在如下几方面: ——把未知化归为已知,例如用诱导公式把求任意角的三角函数值逐步化归为求锐角三角函数值 ——把特殊化归为一般,例如把正弦函数的图象逐步化归为函数y=Asin(ωx+),x∈R,(其中 A>0,ω>0)的简图,把已知三角函数值求角化归为[0,2π]上适合条件的角的集合等 ——等价化归,例如进行三角函数式的化简、恒等变形和证明三角恒等式 三、讲解范例: 例1 化简cos(π+α)+cos(π-α),其中k∈Z 解法一: 原式=cos[kπ+(+α)]+cos[kπ-(+α)] =coskπcos(+α)-sinkπsin(+α)+coskπcos(+α) +sinkπsin(+α)=2coskπcos(+α),(k∈Z) 当k为偶数时,原式=2cos(+α)=cosα-sinα 当k为奇数时,原式=-2cos(+α)=sinα-cosα 总之,原式=(-1)k(cosα-sinα),k∈Z 解法二:由(kπ++α)+(kπ--α)=2kπ,知 cos(kπ--α)=cos[2kπ-(+α+kπ)] =cos[-(kπ++α)]=cos(kπ++α) ∴原式=2cos(kπ++α)=2×(-1)kcos(+α) =(-1)k(cosα-sinα),其中k∈Z 评述:原式=cos(kπ++α)+cos(kπ--α)=cos[kπ+(+α)]+cos[kπ-(+α)] 这就启发我们用余弦的和(差)角公式 例2 已知sin(α+β)=,cos(α-β)=,求的值 解法一:由已知条件及正弦的和(差)角公式, 解法二:(设未知数)令x= 解之得 例3已知函数y=Asin(ωx+),x∈R,(其中A>0,ω>0)的图象在y轴右侧的第一个最高点(函数取最大值的点)为M(2,2),与x轴在原点右侧的第一个交点为N(6,0),求这个函数的解析式 解法一:根据题意,可知=6-2=4 ∴T=16,∴ω= 将点M的坐标(2,2)代入y=2sin(x+), 得2=2sin(×2+) 即sin(+)=1 ∴满足+=的的最小正数解,即= 从而所求的函数解析式是 y=2sin(x+),x∈R 解法二:将两个点M(2,2),N(6,0)的坐标分别代入y=2sin(ωx+φ)并化简 ∴在长度为一个周期且包含原点的闭区间上,有 ∴所求的函数解析式是y=2sin(x+),x∈R 四、小结:通过本节学习,大家要系统掌握三角函数有关知识,并能灵活应用其进行三角函数式的化简、求值、证明,并能解决一些实际问题等等 五、课后作业: 六、板书设计(略) 七、课后记: 数学公式变形要讲究“三有” 数学公式教学是中学数学教学的重要组成部分,为了理解公式的内在本质,就要进行适当的变形,但要讲究“三有”,即:变之有用,变之有规,变之有益 1公式变形的目的最终应体现在其实用的价值,一个公式的等价变形往往有多种,教学中应择其有用的变形,以提高应用公式的效能 2数学公式变形的方法多种多样,揭示数学公式变形的一般规律对深化公式教学会有积极的意义由于公式中的字母可以代表数、式、函数等有数学意义的式子,因此可以根据需要对公式进行适当的数学处理,或代换,或迭代,或取特殊值等等 3公式变形不仅仅是标准公式功能的拓宽,而且在变形过程中可以充分体现数学思想和观点,充分体现数学公式的转化和简化功能,使学生深刻理解数学公式的本质 例如对于公式= 变形一:用-β代换β得到 = 用α=45°代入得到 变形二:当α=β时,tan2α= 当α=π时,tan(π+β)=tanβ 当α=2π时,用-β代换β时 tan(2π-β)=-tanβ (用特殊值代入原公式是公式变形,发现新、旧公式之间关系所常用的办法) 变形三:tan(α+β+γ)= 由此引申为 α+β+γ=kπ(k∈Z)tanα+tanβ+tanγ=tanαtanβtanγ (对原公式进行类比推广是一种常用公式变形的方法) (注意到原公式是涉及tanαtanβ、tanα+tanβ、tan(α+β)、1的一个方程,因此从方程观点出发进行变形更是一种行之有效的变形办法,由此产生逆变公式、整体变换公式等等)查看更多