江西专版2020中考数学复习方案第三单元函数第13课时二次函数的图象与性质二课件
第
13
课时
二次函数的图象与性质
(
二
)
第三单元 函数
【
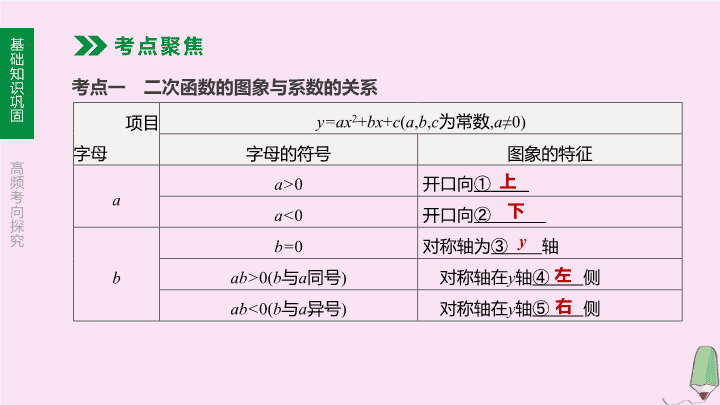
考情分析
】
高频考点
年份、题号、分值
题型
2020
年中考预测
二次函数、方程
与不等式
2017
、
22(1)
、
3
分
解答题
★★★
2015
、
23(3)
、
3
分
2013
、
6
、
3
分
选择题
二次函数有关
变量系数的
综合探究
2017
、
22(1)(2)
、
4
分
解答题
★★★★★
2015
、
23(1)
、
2
分
2014
、
24(1)(2)
、
6
分
2014
、
6
、
3
分
选择题
2013
、
24(1)(2)
、
6
分
解答题
考点一 二次函数的图象与系数的关系
考点聚焦
项目
字母
y=ax
2
+
bx
+
c
(
a
,
b
,
c
为常数
,
a
≠0)
字母的符号
图象的特征
a
a>
0
开口向
①
a<
0
开口向
②
b
b=
0
对称轴为
③
轴
ab>
0(
b
与
a
同号
)
对称轴在
y
轴
④
侧
ab<
0(
b
与
a
异号
)
对称轴在
y
轴
⑤
侧
上
下
y
左
右
项目
字母
字母的符号
图象的特征
c
c=
0
经过点
⑥
c>
0
与
y
轴
⑦
相交
c<
0
与
y
轴
⑧
相交
b
2
-4
ac
b
2
-4
ac=
0
与
x
轴有唯一交点
(
顶点
)
b
2
-4
ac>
0
与
x
轴有
⑨
个不同的交点
b
2
-4
ac<
0
与
x
轴没有交点
(
续表
)
(0,0)
正半轴
负半轴
两
项目
字母
字母的符号
图象的特征
特殊
关系
当
x=
1
时
,
y=a
+
b
+
c
当
x=
-1
时
,
y=
⑩
若
a
+
b
+
c>
0,
则当
x=
1
时
,
y>
0
若
a
-
b
+
c>
0,
则当
x=
⑪
时
,
y>
0
(
续表
)
a
-
b
+
c
-1
抛物线
y=ax
2
+
bx
+
c
与
x
轴的
交点个数
判别式
b
2
-4
ac
的正负
方程
ax
2
+
bx
+
c=
0
的实数根个数
2
个
b
2
-4
ac>
0
两个
⑫
的实数根
1
个
b
2
-4
ac=
0
两个
⑬
的实数根
没有
b
2
-4
ac<
0
⑭
实数根
考点二 二次函数与一元二次方程、不等式的关系
1
.
二次函数与一元二次方程的关系
不相等
相等
没有
2
.
二次函数与不等式的关系
(1)
ax
2
+
bx
+
c>
0
的解集
函数
y=ax
2
+
bx
+
c
的图象位于
x
轴上方的部分对应的点的横坐标的取值范围
.
(2)
ax
2
+
bx
+
c<
0
的解集
函数
y=ax
2
+
bx
+
c
的图象位于
⑮
的部分对应的点的横坐标的取值范围
.
x
轴下方
1
.
[2019·
荆门
]
抛物线
y=
-
x
2
+4
x
-4
与坐标轴的交点个数为
(
)
A
.
0 B
.
1 C
.
2 D
.
3
题组一 必会题
对点演练
C
2
.
二次函数
y=ax
2
+
bx
+
c
(
a
≠0)
的图象如图
13-1,
下列结论
:
①
b
2
>
4
ac
;
②
abc<
0;
③
2
a
+
b
-
c>
0;
④
a
+
b
+
c<
0
.
其中正确的是
.
(
填序号
)
图
13-1
①④
3
.
二次函数
y=x
2
-
x
-6
的图象如图
13-2,
观察图象回答
:
(1)
当
时
,
y>
0;(2)
当
时
,
y=
0;
(3)
当
时
,
y<
0
.
图
13-2
x<
-2
或
x>
3
x=
-2
或
x=
3
-2
1)
的图象与
x
轴交点的判断
,
正确的是
(
)
A
.
没有交点
B
.
只有一个交点
,
且它位于
y
轴右侧
C
.
有两个交点
,
且它们均位于
y
轴左侧
D
.
有两个交点
,
且它们均位于
y
轴右侧
D
6
.
[2018·
莱芜
]
函数
y=ax
2
+2
ax
+
m
(
a<
0)
的图象过点
(2,0),
则使函数值
y<
0
成立的
x
的取值范围是
(
)
A
.x<
-4
或
x>
2 B
.
-4
2 D
.
0
2
时
y<
0
.
7
.
已知二次函数
y=kx
2
-(2
k
-1)
x
+
k
-2
的图象与
x
轴交于两个不同的点
,
那么
k
的取值范围是
.
考向一 二次函数的图象与各项系数的关系
例
1
[2018·
恩施州
]
抛物线
y=ax
2
+
bx
+
c
的对称轴为直线
x=
-1,
部分图象如图
13-3,
下列判断
:
①
abc>
0;
②
b
2
-4
ac>
0;
③
9
a
-3
b
+
c=
0;
④若点
(-0
.
5,
y
1
),(-2,
y
2
)
均在抛物线上
,
则
y
1
>y
2
;
⑤
5
a
-2
b
+
c<
0,
其中正确的个数为
(
)
A
.
2 B
.
3 C
.
4 D
.
5
图
13-3
[
答案
]
B
【
方法点析
】
利用图象位置来判断系数的符号
,
或者含有系数的关系式
(
a
的符号由开口方向决定
,
c
的符号由抛物线与
y
轴交点的位置确定
,
b
的符号由
a
及对称轴的位置确定
,
抛物线与
x
轴交点的个数决定根的判别式的符号
)
时
,
常利用数形结合思想
,
通过对开口方向以及对称轴位置
,
与坐标轴的交点位置、顶点和其他特殊点位置的
“
量化
”
分析
,
得到关系式
.
|
考向精练
|
1
.
[2019·
益阳
]
已知二次函数
y=ax
2
+
bx
+
c
的图象如图
13-4,
下列结论
:
①
ac<
0,
②
b
-2
a<
0,
③
b
2
-4
ac<
0,
④
a
-
b
+
c<
0,
正确的是
(
)
A
.
①②
B
.
①④
C
.
②③
D
.
②④
图
13-4
[
答案
]
A
2
.
[2019·
甘肃
]
如图
13-5
是二次函数
y=ax
2
+
bx
+
c
的图象
,
对于下列说法
:
①
ac>
0,
②
2
a
+
b>
0,
③
4
ac
0
时
,
y
随
x
的增大而减小
,
其中正确的是
(
)
A
.
①②③
B
.
①②④
C
.
②③④
D
.
③④⑤
图
13-5
[
答案
]
C
图
13-6
[
答案
]
D
考向二 借助图象求解二次函数、方程与不等式之间的关系
例
2
[2019·
潍坊
]
抛物线
y=x
2
+
bx
+3
的对称轴为直线
x=
1
.
若关于
x
的一元二次方程
x
2
+
bx
+3-
t=
0(
t
为实数
)
在
-1
2
a
;
③
ax
2
+
bx
+
c=
0
的两根分别为
-3
和
1;
④
a
-2
b
+
c>
0
.
其中正确的命题是
(
)
A
.
①②
B
.
②③
C
.
①③
D
.
①②③④
图
13-7
[
答案
]
C
2
.
[2019·
威海
]
在画二次函数
y=ax
2
+
bx
+
c
(
a
≠0)
的图象时
,
甲写错了一次项的系数
,
列表如下
:
乙写错了常数项
,
列表如下
:
通过上述信息
,
解决以下问题
:
(1)
求原二次函数
y=ax
2
+
bx
+
c
(
a
≠0)
的表达式
;
(2)
对于二次函数
y=ax
2
+
bx
+
c
(
a
≠0),
当
x
时
,
y
的值随
x
的值增大而增大
;
(3)
若关于
x
的方程
ax
2
+
bx
+
c=k
(
a
≠0)
有两个不相等的实数根
,
求
k
的取值范围
.
x
…
-1
0
1
2
3
…
y
甲
…
6
3
2
3
6
…
x
…
-1
0
1
2
3
…
y
乙
…
-2
-1
2
7
14
…
2
.
[2019·
威海
]
在画二次函数
y=ax
2
+
bx
+
c
(
a
≠0)
的图象时
,
甲写错了一次项的系数
,
列表如下
:
乙写错了常数项
,
列表如下
:
通过上述信息
,
解决以下问题
:
(2)
对于二次函数
y=ax
2
+
bx
+
c
(
a
≠0),
当
x
时
,
y
的值随
x
的值增大而增大
;
x
…
-1
0
1
2
3
…
y
甲
…
6
3
2
3
6
…
x
…
-1
0
1
2
3
…
y
乙
…
-2
-1
2
7
14
…
(2)
抛物线
y=x
2
+2
x
+3
的对称轴为直线
x=
-1
.
∵二次项系数为
1,
故抛物线开口向上
,
∴当
x
≥-1
时
,
y
的值随
x
值的增大而增大
.
故答案为
≥-1
.
2
.
[2019·
威海
]
在画二次函数
y=ax
2
+
bx
+
c
(
a
≠0)
的图象时
,
甲写错了一次项的系数
,
列表如下
:
乙写错了常数项
,
列表如下
:
通过上述信息
,
解决以下问题
:
(3)
若关于
x
的方程
ax
2
+
bx
+
c=k
(
a
≠0)
有两个不相等的实数根
,
求
k
的取值范围
.
x
…
-1
0
1
2
3
…
y
甲
…
6
3
2
3
6
…
x
…
-1
0
1
2
3
…
y
乙
…
-2
-1
2
7
14
…
(3)
∵方程
ax
2
+
bx
+
c=k
(
a
≠0)
有两个不相等的实数根
,
即
x
2
+2
x
+3-
k=
0
有两个不相等的实数根
,
∴
Δ=
4-4(3-
k
)
>
0,
解得
k>
2
.
考向三 与变量系数有关的二次函数综合题
例
3
[2017·
湖北
]
已知函数
y=mx
2
-6
x
+1(
m
是常数
)
.
(1)
求证
:
不论
m
为何值
,
该函数的图象都经过
y
轴上的一个定点
;
(2)
当该函数的图象与
x
轴有两个交点时
,
求
m
的取值范围
,
并求
m
为最大整数时
,
方程
mx
2
-6
x
+1
=
0(
m
是常数
)
的两根
;
(3)
若该函数的图象与
x
轴只有一个交点
,
求
m
的值
.
解
:(1)
证明
:
当
x=
0
时
,
y=
1
.
所以不论
m
为何值
,
函数
y=mx
2
-6
x
+1
的图象都经过
y
轴上的一个定点
(0,1)
.
例
3
[2017·
湖北
]
已知函数
y=mx
2
-6
x
+1(
m
是常数
)
.
(2)
当该函数的图象与
x
轴有两个交点时
,
求
m
的取值范围
,
并求
m
为最大整数时
,
方程
mx
2
-6
x
+1
=
0(
m
是常数
)
的两根
;
例
3
[2017·
湖北
]
已知函数
y=mx
2
-6
x
+1(
m
是常数
)
.
(3)
若该函数的图象与
x
轴只有一个交点
,
求
m
的值
.
(3)
当
m=
0
时
,
函数
y=
-6
x
+1
的图象与
x
轴只有一个交点
;
当
m
≠0
时
,
若函数
y=mx
2
-6
x
+1
的图象与
x
轴只有一个交点
,
则方程
mx
2
-6
x
+1
=
0
有两个相等的实数根
,
所以
(-6)
2
-4
m=
0,
解得
m=
9
.
综上
,
若函数
y=mx
2
-6
x
+1
的图象与
x
轴只有一个交点
,
则
m
的值为
0
或
9
.
|
考向精练
|
[2012·
江西
23
题
]
如图
13-8,
已知二次函数
L
1
:
y=x
2
-4
x
+3
的图象与
x
轴交于
A
,
B
两点
(
点
A
在点
B
的左边
),
与
y
轴交于点
C.
(1)
写出
A
,
B
点坐标
.
(2)
二次函数
L
2
:
y=kx
2
-4
kx
+3
k
(
k
≠0)
图象的顶点为
P.
①直接写出二次函数
L
2
与二次函数
L
1
有关图象的
两条相同的性质
.
②是否存在实数
k
,
使
△
ABP
为等边三角形
?
若存在
,
请求出
k
的值
;
若不存在
,
请说明理由
.
图
13-8
③若直线
y=
8
k
与抛物线
L
2
交于点
E
,
F
,
请问线段
EF
的长度是否会发生变化
?
如果不会
,
求
EF
的长度
;
如果会
,
说明理由
.
解
:(1)
A
(1,0),
B
(3,0)
.
[2012·
江西
23
题
]
如图
13-8,
已知二次函数
L
1
:
y=x
2
-4
x
+3
的图象与
x
轴交于
A
,
B
两点
(
点
A
在点
B
的左边
),
与
y
轴交于点
C.
(2)
二次函数
L
2
:
y=kx
2
-4
kx
+3
k
(
k
≠0)
图象的顶点为
P.
①直接写出二次函数
L
2
与二次函数
L
1
有关图象的两条相同的性质
.
图
13-8
(2)
①二次函数
L
2
与
L
1
有关图象的两条相同的性质是
:
对称轴都是直线
x=
2
或顶点的横坐标都为
2;
都经过点
A
(1,0),
B
(3,0)
.
[2012·
江西
23
题
]
如图
13-8,
已知二次函数
L
1
:
y=x
2
-4
x
+3
的图象与
x
轴交于
A
,
B
两点
(
点
A
在点
B
的左边
),
与
y
轴交于点
C.
(2)
二次函数
L
2
:
y=kx
2
-4
kx
+3
k
(
k
≠0)
图象的顶点为
P.
②是否存在实数
k
,
使
△
ABP
为等边三角形
?
若存在
,
请求出
k
的值
;
若不存在
,
请说明理由
.
图
13-8
[2012·
江西
23
题
]
如图
13-8,
已知二次函数
L
1
:
y=x
2
-4
x
+3
的图象与
x
轴交于
A
,
B
两点
(
点
A
在点
B
的左边
),
与
y
轴交于点
C.
(2)
二次函数
L
2
:
y=kx
2
-4
kx
+3
k
(
k
≠0)
图象的顶点为
P.
③若直线
y=
8
k
与抛物线
L
2
交于点
E
,
F
,
请问线段
EF
的长度是否会发生变化
?
如果不会
,
求
EF
的长度
;
如果会
,
说明理由
.
图
13-8
③线段
EF
的长度不会发生变化
.
∵直线
y=
8
k
与抛物线
L
2
交于
E
,
F
两点
,
∴
kx
2
-4
kx
+3
k=
8
k
有两个不相等的实数根
.
∵
k
≠0,
∴
x
2
-4
x
-5
=
0,
∴
x
1
=
-1,
x
2
=
5,
∴
EF=x
2
-
x
1
=
6,
∴线段
EF
的长度不会发生变化
.