二次函数导学案(1)(1) 实际问题与二次函数（3）

二次函数导学案(1)(1) 实际问题与二次函数（3）

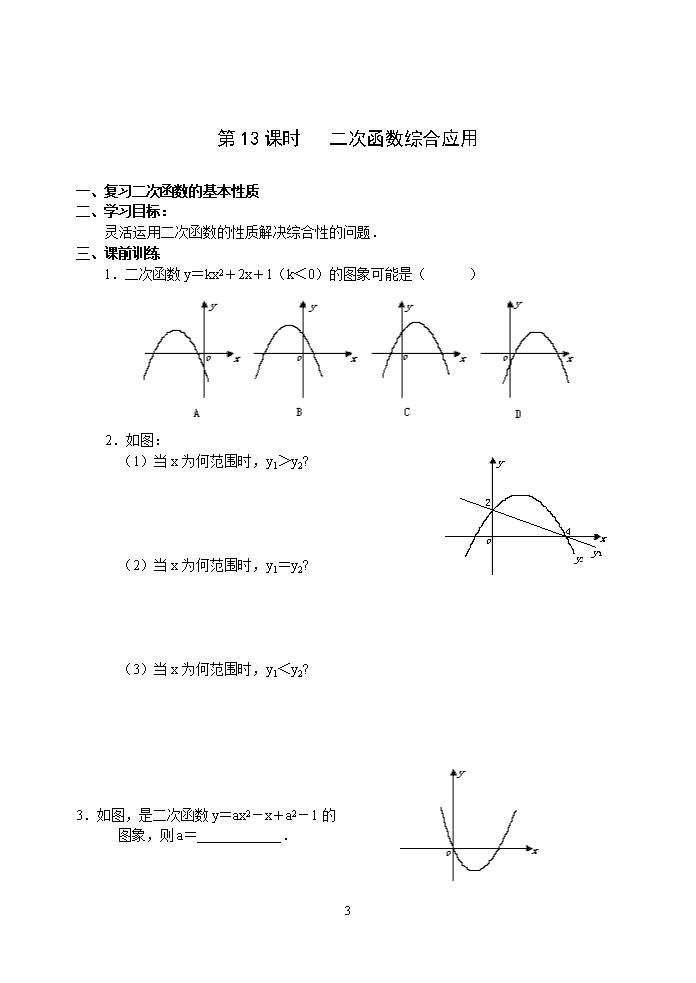
第二十二章 二次函数 第12课时 实际问题与二次函数（3）‎ 一、阅读课本：‎ 二、学习目标：‎ ‎1．会建立直角坐标系解决实际问题；‎ ‎2．会解决桥洞水面宽度问题．‎ 三、基本知识练习 ‎1．以抛物线的顶点为原点，以抛物线的对称轴为y轴建立直角坐标系时，可设这条抛物线 的关系式为___________________________________．‎ ‎2．拱桥呈抛物线形，其函数关系式为y＝－x2，当拱桥下水位线在AB位置时，水面宽为 ‎12m‎，这时水面离桥拱顶端的高度h是（ ）‎ ‎ A．‎3m B．‎2‎m C．‎4‎m D．‎‎9m ‎3．有一抛物线拱桥，已知水位线在AB位置时，水面的宽为‎4‎米，水位上升‎4米，就达到警戒线CD，这时水面宽为‎4‎米．若洪水到来时，水位以每小时‎0.5米的速度上升，则水过警戒线后几小时淹没到拱桥顶端M处？‎ 四、课堂练习 ‎ 1．一座拱桥的轮廓是抛物线（如图①所示），拱高‎6m，跨度‎20m，相邻两支柱间的距离均为‎5m．‎ ‎ （1）将抛物线放在所给的直角坐标系中（如图②所示），其关系式y＝ax2＋c的形式，请根据所给的数据求出a、c的值；‎ ‎ （2）求支柱MN的长度；‎ ‎ （3）拱桥下地平面是双向行车道（正中间是一条宽‎2m的隔离带），其中的一条行车道能否并排行驶宽‎2m，高‎3m的三辆汽车（汽车间的间隔忽略不计）？请说说你的理由．‎ 图①‎ 4‎ ‎ 2．如图，有一座抛物线形拱桥，在正常水位时水面AB的宽为‎20m，如果水位上升‎3m时，水面CD的宽是‎10m．‎ ‎ （1）建立如图所示的直角坐标系，求此抛物线的解析式．‎ ‎ （2）现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地，已知甲地距此桥‎280km（桥长忽略不计）．货车正以每小时‎40km的速度开往乙地，当行驶1h时，忽然接到紧急通知：前方连降暴雨，造成水位以每小‎0.25m的速度持续上涨（货车接到通知时水位在CD处，当水位达到桥拱最高点O时，禁止车辆通行）．试问：如果货车按原来速度行驶，能否安全通过此桥？若能，请说明理由．若不能，要使货车安全通过此桥，速度应超过每小时多少千米？‎ 4‎ 第13课时 二次函数综合应用 一、复习二次函数的基本性质 二、学习目标：‎ 灵活运用二次函数的性质解决综合性的问题．‎ 三、课前训练 ‎1．二次函数y＝kx2＋2x＋1（k＜0）的图象可能是（ ）‎ ‎2．如图：‎ ‎ （1）当x为何范围时，y1＞y2?‎ ‎ （2）当x为何范围时，y1＝y2?‎ ‎ （3）当x为何范围时，y1＜y2?‎ ‎3．如图，是二次函数y＝ax2－x＋a2－1的 图象，则a＝____________．‎ 4‎ ‎4．若A（－，y1），B（－1，y2），C（，y3）为二次函数y＝－x2－4x＋5图象上的三点，则y1、y2、y3的大小关系是（ ）‎ A．y1＜y2＜y3 B．y3＜y2＜y‎1 ‎ C．y3＜y1＜y2 D．y2＜y1＜y3‎ ‎5．抛物线y＝(x－2) (x＋5)与坐标轴的交点分别为A、B、C，则△ABC的面积为__________．‎ ‎6．如图，已知在平面直角坐标系中，矩形ABCD的边AD在x轴上，点A在原点，AB＝3，AD＝5．若矩形以每秒2个单位长度沿x轴正方向做匀速运动，同时点P从A点出发以每秒1个单位长度沿A→B→C→D的路线做匀速运动．当点P运动到点D时停止运动，矩形ABCD也随之停止运动．‎ ‎ （1）求点P从点A运动到点D所需的时间．‎ ‎ （2）设点P运动时间为t（秒）‎ ‎ ①当t＝5时，求出点P的坐标．‎ ‎ ②若△OAP的面积为S，试求出S与 t之间的函数关系式（并写出相应 的自变量t的取值范围）．‎ 五、目标检测 如图，二次函数y＝ax2＋bx＋c的图像经过A（－1，0），B（3，0）两交点，且交y轴于 点C．‎ ‎（1）求b、c的值；‎ ‎（2）过点C作CD∥x轴交抛物线于点D，点M为此抛物线的顶点，试确定△MCD的形状．‎ 4‎