数学人教版八年级上册教案13-4 课题学习 最短路径问题

数学人教版八年级上册教案13-4 课题学习 最短路径问题

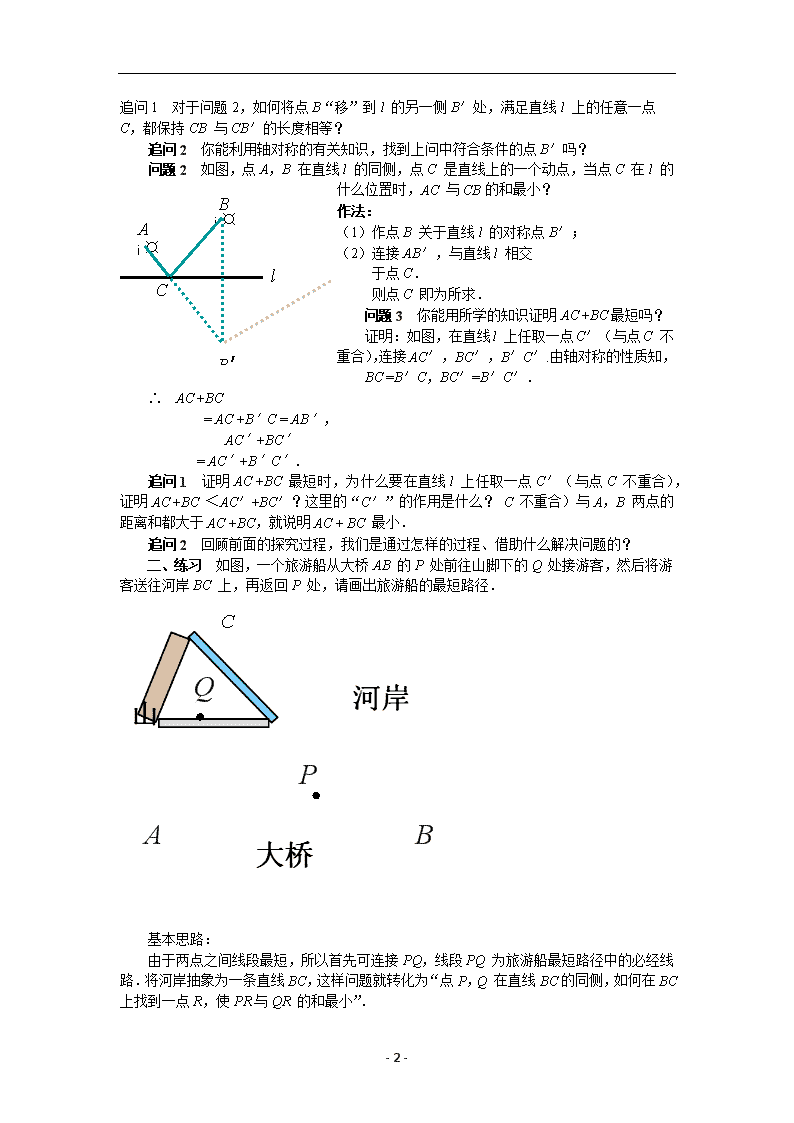
- 1 - 13.4 课题学习 最短路径问题 教学目标： 1、能利用轴对称解决简单的最短路径问题. 2、体会图形的变化在解决最值问题中的作用. 3、感悟转化思想． 学习重点： 利用轴对称将最短路径问题转化为“两点之间，线段最短”问题． 教学过程 一、探索新知 问题 1 相传，古希腊亚历山大里亚城里有一 位久负盛名的学者，名叫海伦．有一天，一位将 军专程拜访海伦，求教一个百思不得其解的问题： 从图中的 A 地出发，到一条笔直的河边 l 饮马，然后到 B 地．到河边什么地方饮马可 使他所走的路线全程最短？精通数学、物理学的海伦稍加思索，利用轴对称的知识回答了这 个问题．这个问题后来被称为“将军饮马问题”．你能将这个问题抽象为数学问题吗？ 追问 2 你能用自己的语言说明这个问题的意思，并把它抽象为数学问题吗？ （1）从 A 地出发，到河边 l 饮马，然后到 B 地； （2）在河边饮马的地点有无穷多处，把这些地点与 A， B 连接起来的两条线段的长度 之和，就是从 A 地到饮马地点，再回到 B 地的路程之和； （3）现在的问题是怎样找出使两条线段长度之和为最 短的直线 l 上的点．设 C 为 直线上的一个动点，上面的问题就转化为：当点 C 在 l 的什么位置时， AC 与 CB 的和最 小（如图）． 问题 2 如图，点 A，B 在直线 l 的同侧，点 C 是直线上的一个动点，当点 C 在 l 的 什么位置时，AC 与 CB 的和最小？ 追问 1 对于问题 2，如何将点 B“移”到 l 的另一侧 B′处，满足直线 l 上的任意一点 B¡¤ ¡¤A l B A l - 2 - C，都保持 CB 与 CB′的长度相等？ 追问 2 你能利用轴对称的有关知识，找到上问中符合条件的点 B′吗？ 问题 2 如图，点 A，B 在直线 l 的同侧，点 C 是直线上的一个动点，当点 C 在 l 的 什么位置时，AC 与 CB 的和最小？ 作法： （1）作点 B 关于直线 l 的对称点 B′； （2）连接 AB′，与直线 l 相交 于点 C． 则点 C 即为所求． 问题 3 你能用所学的知识证明 AC +BC 最短吗？ 证明：如图，在直线 l 上任取一点 C′（与点 C 不 重合），连接 AC′，BC′，B′C′.由轴对称的性质知， BC =B′C，BC′=B′C′． ∴ AC +BC = AC +B′C = AB′， AC′+BC′ = AC′+B′C′． 追问 1 证明 AC +BC 最短时，为什么要在直线 l 上任取一点 C′（与点 C 不重合）， 证明 AC +BC ＜AC′+BC′？这里的“C′”的作用是什么？ C 不重合）与 A，B 两点的 距离和都大于 AC +BC，就说明 AC + BC 最小． 追问 2 回顾前面的探究过程，我们是通过怎样的过程、借助什么解决问题的？ 二、练习 如图，一个旅游船从大桥 AB 的 P 处前往山脚下的 Q 处接游客，然后将游 客送往河岸 BC 上，再返回 P 处，请画出旅游船的最短路径． 基本思路： 由于两点之间线段最短，所以首先可连接 PQ，线段 PQ 为旅游船最短路径中的必经线 路．将河岸抽象为一条直线 BC，这样问题就转化为“点 P，Q 在直线 BC 的同侧，如何在 BC 上找到一点 R，使 PR 与 QR 的和最小”． 三、归纳小结 A B C P Q山 河岸 大桥 - 3 - 1、本节课研究问题的基本过程是什么？ 2、轴对称在所研究问题中起什么作用？ 四、布置作业 教科书 P93 复习题 13 第 15 题.