- 2021-05-28 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学一轮复习知识点+题型专题讲义13 二次函数(学生版)
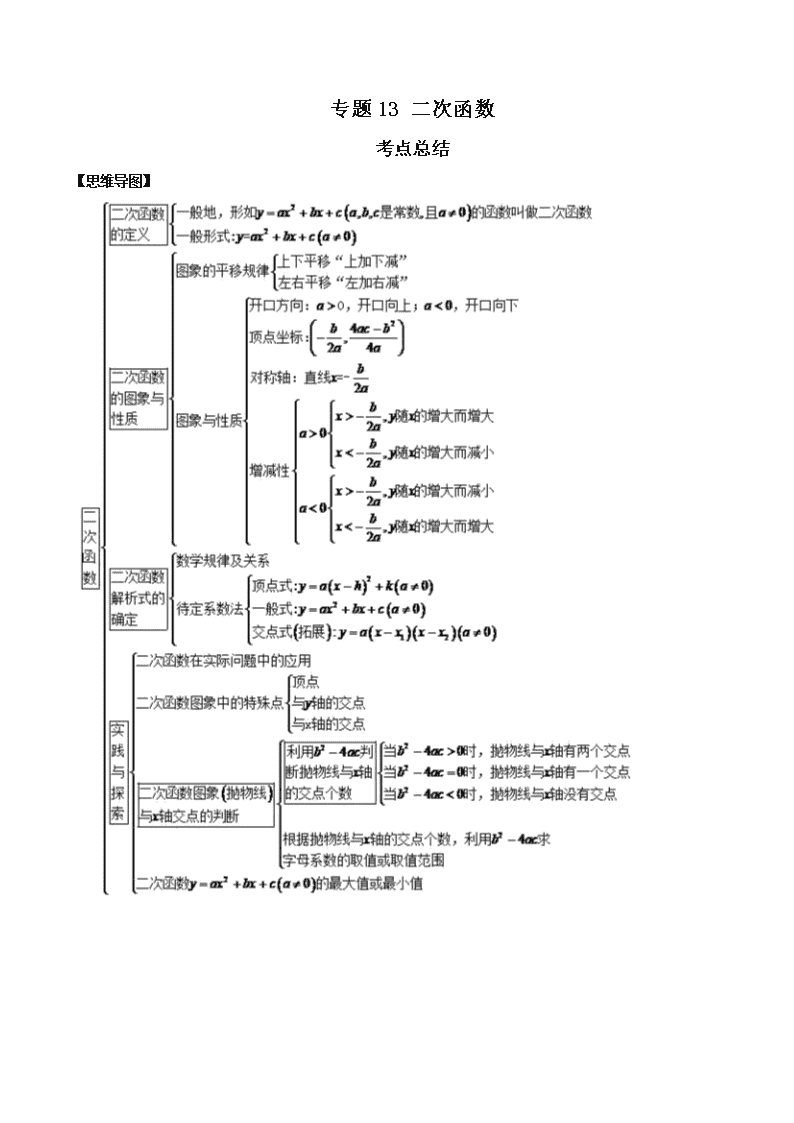
专题 13 二次函数 考点总结 【思维导图】 【知识要点】 知识点一 二次函数的概念 概念:一般地,形如 � 文 细� � � ܾ� � � ( 细� , ��ܾ� , ��� 是常数, 细 � � )的函数,叫做二次函数。 注意:二次项系数 细 � � ,而 ܾ , � 可以为零. 二次函数 � 文 函� � � ࢈� � � 的结构特征: ⑴ 等号左边是函数,右边是关于自变量 x 的二次式,x 的最高次数是 2. ⑵ 细� , ܾ� , � 是常数, 细 是二次项系数, ܾ 是一次项系数, � 是常数项. 1.(2017·甘肃中考模拟)下列函数中,是二次函数的有( ) ① � 文 㘵 ⸲ �� � ② � 文 㘵 � � ③ � 文 � 㘵 ⸲ � ④ � 文 㘵 ⸲ �� 㘵 � ��A.1 个 B.2 个 C.3 个 D.4 个 2.(2013·湖南中考真题)下列函数是二次函数的是( ) A.y 文 � x � 㘵 B.y 文⸲ � x � 㘵 C.y 文 x � � � D.y 文 㘵 � x ⸲ �3.(2018·安徽中考模拟)下列函数不属于二次函数的是( ) A. � 文 � ⸲ 㘵 � � � B. 21y x 12 C. � 文 㘵 ⸲ �� � D. 2 2y 2 x 3 2x 4.(2018·上海中考模拟)下列函数中是二次函数的是( ) A.y=2(x﹣1) B.y=(x﹣1)2﹣x2 C.y=a(x﹣1)2 D.y=2x2﹣1 考查题型一 待定系数法求二次函数解析式 1.(2018·广东中考模拟)二次函数 y=ax2+bx+c 的自变量 x 与函数 y 的对应值如下表: x … -5 -4 -3 -2 -1 0 … y … 4 0 -2 -2 0 4 … 下列说法正确的是( ) A.抛物线的开口向下 B.当 x>-3 时,y 随 x 的增大而增大 C.二次函数的最小值是-2 D.抛物线的对称轴是直线 x=- � �2.(2018·上海中考模拟)已知二次函数 y=ax2+bx+c 的图象上部分点的横坐标 x 与纵坐标 y 的对应值如 下表: x … -1 0 1 2 … y … 0 3 4 3 … 那么关于它的图象,下列判断正确的是( ) A.开口向上 B.与 x 轴的另一个交点是(3,0) C.与 y 轴交于负半轴 D.在直线 x=1 的左侧部分是下降的 考查题型二 根据二次函数的定义求参数值 1.(2012·山东中考真题)抛物线 y 文 ax � � bx ⸲ � 经过点(2,4),则代数式 � a � � b � 㘵 的值为( ) A.3 B.9 C. 㘵� D. ⸲ 㘵�2.(2018·安徽中考模拟)已知函数 y=(m2﹣m)x2+(m﹣1)x+m+1. (1)若这个函数是一次函数,求 m 的值; (2)若这个函数是二次函数,则 m 的值应怎样? 知识点 2:二次函数的图象和性质(重点) 二次函数的基本表现形式: ① � 文 细� � ;② � 文 细� � � � ;③ � 文 细 � ⸲ ㄷ � ;④ � 文 细 � ⸲ ㄷ � � � ;⑤ � 文 细� � � ܾ� � � . 第一种:二次函数 � 文 函� � 的性质(最基础) 1.(2019·辽宁中考模拟)下列关于二次函数 22y x 的说法正确的是( ) A.它的图象经过点 � ⸲ 㘵ͳ ⸲ ��B.它的图象的对称轴是直线 � 文 �C.当 0x 时, � 随 � 的增大而减小 D.当 � 文 � 时, � 有最大值为 0 2.(2019·山东中考模拟)给出下列函数:①y=2x﹣3;②y= 㘵 � ;③y=2x2;④y=﹣3x+1.上述函数中符合 条件“当 x>0 时,函数值 y 随自变量 x 增大而减小”的是( ) A.①③ B.③④ C.②④ D.②③ 第二种:二次函数 � 文 函� � � � 的性质 1.(2013·江苏中考模拟)关于二次函数 y=2x2+3,下列说法中正确的是 ( ) A.它的开口方向是向下 B.当 x<-1 时,y 随 x 的增大而减小 C.它的顶点坐标是(2,3) D.当 x=0 时,y 有最大值是 3 2.(2017·黑龙江中考模拟)二次函数 � 文 �� � ⸲ � 的图象是一条抛物线,下列关于该抛物线的说法正确的 是( ) A.抛物线开口向下 B.抛物线与 � 轴有两个交点 C.抛物线的对称轴是直线 � =1 D.抛物线经过点(2,3) 3.(2019·山东中考真题)已知抛物线 y=-x2+1,下列结论: ①抛物线开口向上; 细 的符号 开口方向 顶点坐标 对称轴 性质 细 锘 � 向上 � , � � 轴 � 锘 � 时, � 随 � 的增大而增大; � 增 � 时, � 随 � 的增大 而减小; � 文 � 时, � 有最小值 � . 细 增 � 向下 � , � � 轴 � 锘 � 时, � 随 � 的增大而减小; � 增 � 时, � 随 � 的增大 而增大; � 文 � 时, � 有最大值 � . 细 的符号 开口方向 顶点坐标 对称轴 性质 细 锘 � 向上 � , � � 轴 � 锘 � 时, � 随 � 的增大而增大; � 增 � 时, � 随 � 的增大 而减小; � 文 � 时, � 有最小值 � . 细 增 � 向下 � , � � 轴 � 锘 � 时, � 随 � 的增大而减小; � 增 � 时, � 随 � 的增大 而增大; � 文 � 时, � 有最大值 � . ②抛物线与 x 轴交于点(-1,0)和点(1,0); ③抛物线的对称轴是 y 轴; ④抛物线的顶点坐标是(0,1); ⑤抛物线 y=-x2+1 是由抛物线 y=-x2 向上平移 1 个单位得到的. 其中正确的个数有( ) A.5 个 B.4 个 C.3 个 D.2 个 4.(2018·河北中考模拟)在平面直角坐标系 xOy 中,抛物线 y=﹣x2+2x.点 D(n,y1),E(3,y2)在抛 物线上,若 y1<y2,则 n 的取值范围是( ) A.n>3 或 n<﹣1 B.n>3 C.n<1 D.n>3 或 n<1 第三种:二次函数 � 文 函 � − � � 的性质 1(2019·四川中考模拟)对于函数 y=-2(x-3)2,下列说法不正确的是( ) A.开口向下 B.对称轴是 � 文 � C.最大值为 0 D.与 y 轴不相交 2(2019·湖北中考模拟)关于二次函数 y= 㘵 � (x+1)2 的图象,下列说法正确的是( ) A.开口向下 B.经过原点 C.对称轴右侧的部分是下降的 D.顶点坐标是(﹣1,0) 3(2019·山东中考模拟)在平面直角坐标系中,二次函数 � 文 细�� ⸲ h � � ( 细 � � )的图象可能是( ) A. B. C. D. 第四种:二次函数 � 文 函 � − � � � � 的性质 细 的符号 开口方 向 顶点坐标 对称轴 性质 细 锘 � 向上 h , � X=h � 锘 h 时, � 随 � 的增大而增大; � 增 ㄷ 时, � 随 � 的增大 而减小; � 文 ㄷ 时, � 有最小值 � . 细 增 � 向下 h , � X=h � 锘 h 时, � 随 � 的增大而减小; � 增 ㄷ 时, � 随 � 的增大 而增大; � 文 ㄷ 时, � 有最大值 � . 细 的符号 开口方 顶点坐标 对称轴 性质 二次函数 � 文 细� � � ܾ� � � 用配方法可化成: � 文 细 � ⸲ ㄷ � � � 的形式,其中 h 文 − ܾ �细 , � 文 �细� − ܾ � �细 . 1.2019·广东中考模拟)关于抛物线 � 文 ��� ⸲ 㘵� � � 㘵 ,下列说法错误..的是( ). A.开口向上 B.与 � 轴只有一个交点 C.对称轴是直线 � 文 㘵 D.当 � 锘 㘵 时, � 随 � 的增大而增大 2.2019·广西中考模拟)将 � 文 � � ⸲ � � 㘵 化成 � 文 ( � ⸲ ㄷ ) � � � 的形式,则 ㄷ � � 的值是( ) A.-5 B.-8 C.-11 D.5 3(2019·江苏中考模拟)已知二次函数 y=(x﹣h)2+1(h 为常数),在自变量 x 的值满足 1≤x≤3 的情况下, 与其对应的函数值 y 的最小值为 5,则 h 的值为( ) A.1 或﹣5 B.﹣1 或 5 C.1 或﹣3 D.1 或 3 二次函数图象的平移 平移步骤: 将抛物线解析式转化成顶点式 � 文 细 � ⸲ ㄷ � � � ,确定其顶点坐标 ㄷ� , ��� ; 保持抛物线 � 文 细� � 的形状不变,将其顶点平移到 ㄷ� , ��� 处,具体平移方法如下: 平移规律 向 细 锘 � 向上 h , � X=h � 锘 h 时, � 随 � 的增大而增大; � 增 ㄷ 时, � 随 � 的增大而 减小; � 文 ㄷ 时, � 有最小值 � . 细 增 � 向下 h , � X=h � 锘 h 时, � 随 � 的增大而减小; � 增 ㄷ 时, � 随 � 的增大而 增大; � 文 ㄷ 时, � 有最大值 � . 在原有函数的基础上“ ㄷ 值正右移,负左移; � 值正上移,负下移”. 【概括】左加右减,上加下减 1.(2019·辽宁中考模拟)将抛物线 � 文 �� � 向上平移 3 个单位,再向左平移 2 个单位,那么得到的抛物线 的解析式为( ) A. V文- 㘵 � ��9� B. � 文 �� 文 ⸲ 㘵 � ��9� � 文⸲ 㘵 � � � � 9�� C. ⸲ 㘵 � � ⸲ 9� � � ��㘵� D. 23( 2) 3y x 2.(2017·邹平镇第三中学中考模拟)把抛物线 y=- 㘵 � x2 向下平移 1 个单位长度,再向左平移 1 个单位长度, 得到的抛物线解析式为( ) A.y=- 㘵 � (x+1)2+1 B.y=- 㘵 � (x+1)2-1 C.y=- 㘵 � (x-1)2+1 D.y=- 㘵 � (x-1)2-1 3.(2017·广东中考模拟)把抛物线 y=x2+4 先向左平移 1 个单位,再向下平移 3 个单位,所得抛物线的表 达式为( ) A.y=(x+1)2+7 B.y=(x-1)2+7 C.y=(x-1)2+1 D.y=(x+1)2+1 4.(2018·山东中考模拟)将二次函数 y=x2+2x﹣1 的图象沿 x 轴向右平移 2 个单位长度,得到的函数表达式 是( ) A.y=(x+3)2﹣2 B.y=(x+3)2+2 C.y=(x﹣1)2+2 D.y=(x﹣1)2﹣2 5.(2019·浙江中考模拟)将抛物线 y=2(x﹣4)2﹣1 先向左平移 4 个单位长度,再向上平移 2 个单位长度, 平移后所得抛物线的解析式为( ) A.y=2x2+1 B.y=2x2﹣3 C.y=2(x﹣8)2+1 D.y=2(x﹣8)2﹣3 抛物线 � 文 函� � � ࢈� � � 的三要素:开口方向、对称轴、顶点. 求抛物线的顶点、对称轴的方法(难点) 公式法: � 文 细� � � ܾ� � � 文 细 � � ܾ �细 � � �细�⸲ܾ � �细 , ∴顶点是( ⸲ ܾ �细 , �细�⸲ܾ � �细 ),对称轴是直线 � 文 − ܾ �细 . 配方法:运用配方的方法,将抛物线的解析式化为 � 文 细 � ⸲ ㄷ � � � 的形式,得到顶点为( ㄷ , � ),对称 轴是直线 � 文 ㄷ . 【抛物线的性质】由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的 对称轴,对称轴与抛物线的交点是顶点. 用配方法求得的顶点,再用公式法或对称性进行验证,才能做到万无一失. 抛物线 � 文 函� � � ࢈� � � 中, 函ͳ࢈ͳ� 与函数图像的关系(灵活掌握) 二次项系数 细二次函数 � 文 细� � � ܾ� � � 中, 细 作为二次项系数,显然 细 � � . (1) 当 细 锘 � 时,抛物线开口向上, 细 越大,开口越小,反之 细 的值越小,开口越大; (2) 当 细 增 � 时,抛物线开口向下, 细 越小,开口越小,反之 细 的值越大,开口越大. 【总结起来】 函 决定了抛物线开口的大小和方向, 函 的正负决定开口方向, 函 的大小决定开口的大小. 一次项系数 ܾ在二次项系数 细 确定的前提下, ܾ 决定了抛物线的对称轴. ⑴ 在 细 锘 � 的前提下, 当 ܾ 锘 � 时, ⸲ ܾ �细 增 � ,即抛物线的对称轴在 � 轴左侧(a、b 同号); 当 ܾ 文 � 时, ⸲ ܾ �细 文 � ,即抛物线的对称轴就是 � 轴; 当 ܾ 增 � 时, ⸲ ܾ �细 锘 � ,即抛物线对称轴在 � 轴的右侧(a、b 异号). ⑵ 在 细 增 � 的前提下,结论刚好与上述相反,即 当 ܾ 锘 � 时, ⸲ ܾ �细 锘 � ,即抛物线的对称轴在 � 轴右侧(a、b 异号); 当 ܾ 文 � 时, ⸲ ܾ �细 文 � ,即抛物线的对称轴就是 � 轴; 当 ܾ 增 � 时, ⸲ ܾ �细 增 � ,即抛物线对称轴在 � 轴的左侧(a、b 同号). 【总结起来】在 函 确定的前提下, ࢈ 决定了抛物线对称轴的位置. 常数项 �⑴ 当 � 锘 � 时,抛物线与 � 轴的交点在 � 轴上方,即抛物线与 � 轴交点的纵坐标为正; ⑵ 当 � 文 � 时,抛物线与 � 轴的交点为坐标原点,即抛物线与 � 轴交点的纵坐标为 � ; ⑶ 当 � 增 � 时,抛物线与 � 轴的交点在 � 轴下方,即抛物线与 � 轴交点的纵坐标为负. 【总结起来】 � 决定了抛物线与 � 轴交点的位置. 总之,只要 函� , ��࢈� , ��� 都确定,那么这条抛物线就是唯一确定的. 1(2018·天津中考模拟)如图,抛物线 y=ax2+bx+3(a≠0)的对称轴为直线 x=1,如果关于 x 的方程 ax2+bx ﹣8=0(a≠0)的一个根为 4,那么该方程的另一个根为( ) A.﹣4 B.﹣2 C.1 D.3 2(2019·许昌实验中学中考模拟)如图是二次函数 2y=ax +bx+c 的部分图象,由图象可知不等式 ax � �bx�c增�的解集是( ) A.− 㘵增x增� B. x锘� C. x增 − 㘵 且 x锘� D.x<-1 或 x>5 3(2019·广东中考模拟)已知函数 y=ax2+bx+c 的图象如图所示,则关于 x 的方程 ax2+bx+c﹣4=0 的根的情 况是 A.有两个相等的实数根 B.有两个异号的实数根 C.有两个不相等的实数根 D.没有实数根 考查题型三 二次函数函数值大小的判断方法 1.(2019·湖北中考真题)已知点 � ⸲ 㘵ͳm ͳ� 㘵ͳm ͳ� �ͳm ⸲ � � 锘 � 在同一个函数的图象上,这个函数可 能是( ) A. � = � B. � 文⸲ � � C. � = � � D. � =﹣ � � 2.(2019·江苏中考模拟)已知二次函数 � 文 细�� ⸲ �� � � � ,当 � 文 �㘵 时,函数值为 �㘵 ;当 � 文 �� 时,函数 值为 �� ,若 ��㘵 ⸲ �� 锘 ��� ⸲ �� ,则下列表达式正确的是( ) A. �㘵 � �� 锘 � B. �㘵 ⸲ �� 锘 � C. 细��㘵 ⸲ ��� 锘 � D. 细��㘵 � ��� 锘 �3.(2019·河南中考模拟)点 �㘵 − 㘵ͳ�㘵 , �� �ͳ�� , �� �ͳ�� 均在二次函数 � 文⸲ � � � �� � � 的图象上,则 �㘵 , �� , �� 的大小关系是______. 考查题型四 求抛物线顶点、对称轴的方法 1.(2019·浙江中考模拟)关于抛物线 � 文 㘵 � �� � �� � � � ,下列说法正确的是( ) A.对称轴是直线 � 文 � , � 有最小值是 � B.对称轴是直线 细 文⸲ 㘵 , � 有最大值是 �C.对称轴是直线 � 文 � , � 有最大值是 � D.对称轴是直线 细 文⸲ 㘵 , � 有最小值是 �2.(2016·浙江中考模拟)对于二次函数 y=(x﹣1)2+2 的图象,下列说法正确的是( ) A.开口向下 B.顶点坐标是(1,2) C.对称轴是 x=﹣1 D.与 x 轴有两个交点 3.(2019·江苏中考模拟)关于函数 y=﹣(x+2)2﹣1 的图象叙述正确的是( ) A.开口向上 B.顶点(2,﹣1) C.与 y 轴交点为(0,﹣1) D.对称轴为直线 x=﹣2 4.(2019·山东中考模拟)抛物线 � 文 m� � � �m� � 㘵 ( m 为非零实数)的顶点坐标为_____________. 考查题型五 抛物线对称性的应用 1.(2018·普定县白岩镇白岩中学中考模拟)将抛物线 y=x2﹣1 向下平移 8 个单位长度后与 x 轴的两个交点 之间的距离为( ) A.4 B.6 C.8 D.10 2(2018·山东中考模拟)若二次函数 �ͳ� 的图象与 � 轴只有一个交点,那么 m 的值为( ) A.0 B.0 或 2 C.2 或﹣2 D.0,2 或﹣2 3.(2014·黑龙江中考真题)如图,抛物线 y=ax2+2x+c 经过点 A(0,3),B(﹣1,0),请解答下列问题: (1)求抛物线的解析式; (2)抛物线的顶点为点 D,对称轴与 x 轴交于点 E,连接 BD,求 BD 的长. 注:抛物线 y=ax2+bx+c(a≠0)的顶点坐标是(﹣ , ). 考查题型六 二次函数图象特征与系数关系的应用方法 1.(2019·陕西中考模拟)已知二次函数 y=ax2+bx+c 的图像经过点(0,m)、(4、m)、(1,n),若 n<m,则 ( ) A.a>0 且 4a+b=0 B.a<0 且 4a+b=0 C.a>0 且 2a+b=0 D.a<0 且 2a+b=0 2.(2019·广东中考模拟)如图是二次函数 y=ax2+bx+c 图象的一部分,图象过点 A(﹣5,0),对称轴为直 线 x=﹣2,给出四个结论:①abc>0;②4a+b=0;③若点 B(﹣3,y1)、C(﹣4,y2)为函数图象上的两点, 则 y2<y1;④a+b+c=0.其中,正确结论的个数是( ) A.1 B.2 C.3 D.4 4.(2013·广西中考真题)已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac; ②abc>0;③2a﹣b=0;④8a+c<0;⑤9a+3b+c<0,其中结论正确的是 .(填正确结论的序号) 知识点三 抛物线与 � 轴的交点 二次函数 � 文 细� � � ܾ� � � 的图像与 � 轴的两个交点的横坐标 �㘵 、 �� ,是对应一元二次方程 细� � � ܾ� � � 文 �的两个实数根.抛物线与 � 轴的交点情况可以由对应的一元二次方程的根的判别式判定: ①有两个交点 � � 锘 � � 抛物线与 � 轴相交; ②有一个交点(顶点在 � 轴上) � � 文 � � 抛物线与 � 轴相切; ③没有交点 � � 增 � � 抛物线与 � 轴相离. 考查题型七 利用二次函数与 x 轴的交点判断字母的值范围的方法 1.(2018·湖北中考真题)已知二次函数 y=x2﹣x+ 㘵 � m﹣1 的图象与 x 轴有交点,则 m 的取值范围是( ) A.m≤5 B.m≥2 C.m<5 D.m>2 考查题型八 二次函数与一元二次方程、不等式综合应用的方法 1.(2012·江苏中考模拟)若二次函数 � 文 �� − m� � − 㘵 ,当 � � 㘵 时,y 随 x 的增大而减小,则 m 的取值 范围是( ) A. m 文 㘵 B. m 锘 㘵 C. m � 㘵 D. m � 㘵2.(2017·江苏中考模拟)若二次函数 y=(x﹣m)2﹣1,当 x≤3 时,y 随 x 的增大而减小,则 m 的取值范 围是( ) A.m=3 B.m>3 C.m≥3 D.m≤3 3.(2019·四川中考真题)如图,抛物线 � 文 细� � � ܾ� � ��细 � �� 过点 � ⸲ 㘵ͳ�� , ��ͳ�� ,且顶点在第一象限, 设 � 文 � 细 � � ܾ � � ,则 M 的取值范围是___. 考查题型九 二次函数与其他函数结合的应用方法 1.(2019·内蒙古中考模拟)在同一直角坐标系中,一次函数 y=ax+c 和二次函数 y=ax2+c 的图象大致为 ( ) A. B. C. D. 2.(2018·安徽中考模拟)二次函数 � 文 细�� � m� � � � 的图象如图,则一次函数 � 文 m� � � 的图象经过 ( ) A.第一、二、三象限 B.第一、二、四象限 C.第二、三、四象限 D.第一、三、四象限 3.(2018·山东中考模拟)已知二次函数 y=(x+m)2﹣n 的图象如图所示,则一次函数 y=mx+n 与反比例函 数 y= m� � 的图象可能是( ) A. B. C. D. 4.(2019·安徽中考模拟)二次函数 y=a(x﹣m)2﹣n 的图象如图,则一次函数 y=mx+n 的图象经过( ) A.第一、二、三象限 B.第一、二、四象限 C.第二、三、四象限 D.第一、三、四象限 知识点四 根据条件确定二次函数表达式的几种基本思路(重点) 三点式(带入) 1,已知抛物线 y=ax2+bx+c 经过 A( � ,0),B( � � ,0),C(0,-3)三点,求抛物线的解析式。 2,已知抛物线 y=a(x-1)2+4 , 经过点 A(2,3),求抛物线的解析式。 顶点式(顶点坐标(- ܾ �细 , �细�⸲ܾ � �细 )) 1,已知抛物线 y=x2-2ax+a2+b 顶点为 A(2,1),求抛物线的解析式。 2,已知抛物线 y=4(x+a)2-2b 的顶点为(3,1),求抛物线的解析式。 交点式(带入) 1,已知抛物线与 x 轴两个交点分别为(3,0),(5,0),求抛物线 y=(x-a)(x-b)的解析式。 2,已知抛物线线与 x 轴两个交点(4,0),(1,0)求抛物线 y= 㘵 � a(x-2a)(x-b)的解析式。 定点式 1, 在直角坐标系中,不论 a 取何值,抛物线 � 文⸲ 㘵 � � � � �⸲细 � � � �细 ⸲ � 经过 x 轴上一定点 Q,直线 � 文 �细 ⸲ ��� � � 经过点 Q,求抛物线的解析式。 2.抛物线 y= x2 +(2m-2)x-4m 与 x 轴的交点一定经过直线 y=mx+m+4,求抛物线的解析式。 3,抛物线 y=ax2+ax-2 过直线 y=mx-2m+2 上的定点 A,求抛物线的解析式。 知识点五 通过二次函数解决实际问题 考查题型十 借助抛物线图像解决实际问题 1.(2019·山东中考真题)从地面竖直向上抛出一小球,小球的高度 h (单位: m )与小球运动时间 � (单位: s )之间的函数关系如图所示.下列结论:①小球在空中经过的路程是 40m ;②小球抛出 3 秒后,速度越来 越快;③小球抛出 3 秒时速度为 0;④小球的高度 ㄷ 文 ��m 时, � 文 㘵��b .其中正确的是( ) A.①④ B.①② C.②③④ D.②③ 2.(2018·重庆中考模拟)一位篮球运动员在距离篮圈中心水平距离 4m 处起跳投篮,球沿一条抛物线运动, 当球运动的水平距离为 2.5m 时,达到最大高度 3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为 3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( ) A.此抛物线的解析式是 y=﹣ 㘵 � x2+3.5 B.篮圈中心的坐标是(4,3.05) C.此抛物线的顶点坐标是(3.5,0) D.篮球出手时离地面的高度是 2m 考查题型十一 利用直角坐标系解决实际问题 1.(2017·甘肃中考模拟)图(1)是一个横断面为抛物线形状的拱桥,当水面在图(1)位置时,拱顶(拱 桥洞的最高点)离水面 2 m,水面宽 4 m.如图(2)建立平面直角坐标系,则抛物线的关系式是( ) A.y=﹣2x2 B.y=2x2 C.y=﹣0.5x2 D.y=0.5x2 2.(2019·山西中考模拟)如图所示的是抛物线型拱桥,当拱顶离水面 2m 时,水面宽 4m,若水面下降 2m, 则水面宽度增加( ) A. � � � � m B. � �m C. � � ⸲ � m D. �m考查题型十二 利用二次函数求最大面积 1.(2017·江西南昌二中中考模拟)中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另 外三边用长为 30 米的篱笆围成,已知墙长为 18 米(如图所示),设这个苗圃园垂直于墙的一边的长为 x 米. (1)若苗圃园的面积为 72 平方米,求 x; (2)若平行于墙的一边长不小于 8 米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小 值;如果没有,请说明理由; (3)当这个苗圃园的面积不小于 100 平方米时,直接写出 x 的取值范围. 考查题型十三 利用二次函数求最大利润 1.(2013·辽宁中考真题)某商场购进一批单价为 4 元的日用品.若按每件 5 元的价格销售,每月能卖出 3 万件;若按每件 6 元的价格销售,每月能卖出 2 万件,假定每月销售件数 y(件)与价格 x(元/件)之间 满足一次函数关系. (1)试求 y 与 x 之间的函数关系式; (2)当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少? 考查题型十四 利用二次函数解决运动中的几何问题 1.(2019·云南中考模拟)如图,在△ABC 中,∠B=90°,AB=3cm,BC=6cm,动点 P 从点 A 开始沿 AB 向 点 B 以 1cm/s 的速度移动,动点 Q 从点 B 开始沿 BC 向点 C 以 2cm/s 的速度移动,若 P,Q 两点分别从 A,B 两点同时出发,P 点到达 B 点运动停止,则△PBQ 的面积 S 随出发时间 t 的函数关系图象大致是( ) A. B. C. D. 2.(2019·河南中考模拟)如图,正方形 ABCD 的边长为 4,点 P、Q 分别是 CD、AD 的中点,动点 E 从点 A 向点 B 运动,到点 B 时停止运动;同时,动点 F 从点 P 出发,沿 P→D→Q 运动,点 E、F 的运动速度相同.设 点 E 的运动路程为 x,△AEF 的面积为 y,能大致刻画 y 与 x 的函数关系的图象是( ) A. B. C. D. 3.(2019·河南中考模拟)如图,在 ������ 中, �� 文 9�� ,AB=10cm,BC=8cm,点 P 从点 A 沿 AC 向点 C 以 1cm/s 的速度运动,同时点 Q 从点 C 沿 CB 向点 B 以 2cm/s 的速度运动(点 Q 运动到点 B 停止)。则四边形 PABQ 的面积 y( �m � )与运动时间 x(s)之间的函数图象为( ) A. B. C. D.查看更多