八年级数学上册第13章全等三角形易错课堂三课件新版华东师大版

八年级数学上册第13章全等三角形易错课堂三课件新版华东师大版

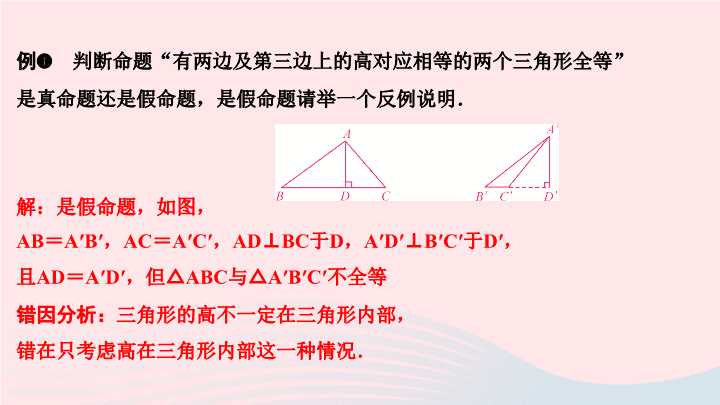
第13章　全等三角形 易错课堂(三)　全等三角形 例 ❶ 　 判断命题 “ 有两边及第三边上的高对应相等的两个三角形全等 ” 是真命题还是假命题，是假命题请举一个反例说明． 解：是假命题，如图， AB ＝ A′B′ ， AC ＝ A′C′ ， AD⊥BC 于 D ， A′D′⊥B′C′ 于 D′ ， 且 AD ＝ A′D′ ，但△ ABC 与△ A′B′C′ 不全等 错因分析： 三角形的高不一定在三角形内部 ， 错在只考虑高在三角形内部这一种情况． 【 对应训练 】 1 ．△ ABC 中， AB ＝ AC ， CD 为 AB 上的高，且△ ADC 为等腰三角形， 则∠ BCD 的度数为 22.5° 或 67.5° ． 2 ．判断命题 “ 有两边及其中一边上的高对应相等的两个三角形全等 ” 是真命题还是假命题，是假命题请举一个反例说明． 解： 假命题，反例如图所示， AD ＝ AC ， BD ＝ CD ， 高为 AE ，△ ABD 与△ ACD 符合条件，但不全等 例 ❷ 　 等腰三角形的一个外角等于 100° ， 则这个等腰三角形的顶角是 ___________ ． 错因分析： 易错在认为 100° 的外角是与等腰三角形顶角相邻的外角 ， 漏掉这个外角也可能是与底角相邻的外角 . 80° 或 20° 【 对应训练 】 3 ．已知一个等腰三角形的两内角的度数之比为 1 ∶ 4 ， 则这个等腰三角形顶角的度数为 ____________ ． 20° 或 120° 例 ❸ 　 如图， AB ＝ AC ， BD ＝ CD ， DE ⊥ BA ，点 E 为垂足， DF ⊥ AC ， 点 F 为垂足．求证： DE ＝ DF. 错因分析： 易错在只由条件利用 “ 边边边 ” 证明 △ ABD 和 △ ACD 全等 ， 根据全等三角形对应角相等可得 ∠ BAD ＝ ∠ CAD ， 直接得出 “ DE ＝ DF ” ， 应该再加上两个条件 “ DE ⊥ BA 于点 E ， DF ⊥ AC 于点 F. ” 【对应训练】 4 ．如图，已知 BE 平分∠ ABC ， CE 平分∠ ACD ，且交 BE 于点 E. 求证： AE 平分∠ FAC. 证明：作 EM⊥AB 于点 M ， EN⊥BC 于点 N ， EK⊥AC 于点 K ， 证 EM ＝ EN ＝ EK 即可得 AE 平分∠ FAC 例 ❹ 　 在△ ABC 中， AB ＝ AC ， AB 的垂直平分线与 AC 所在的直线相交 所得的锐角为 50° ，则∠ B 等于 ______________. 错因分析： 错在只考虑交点在 AC 边上 ， 漏掉交点可能在 CA 的延长线上这种情况． 70° 或 20° 【 对应训练 】 5 ．已知△ ABC 中，∠ A ＝ 50° ，两条高 BD ， CE 所在的直线 相交于点 H ，则∠ BHC 的度数为 _______________ ． 130° 或 50°