- 2021-05-26 发布 |
- 37.5 KB |
- 12页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级数学上册第14章全等三角形14-2三角形全等的判定(第2课时)课件(新版)沪科版
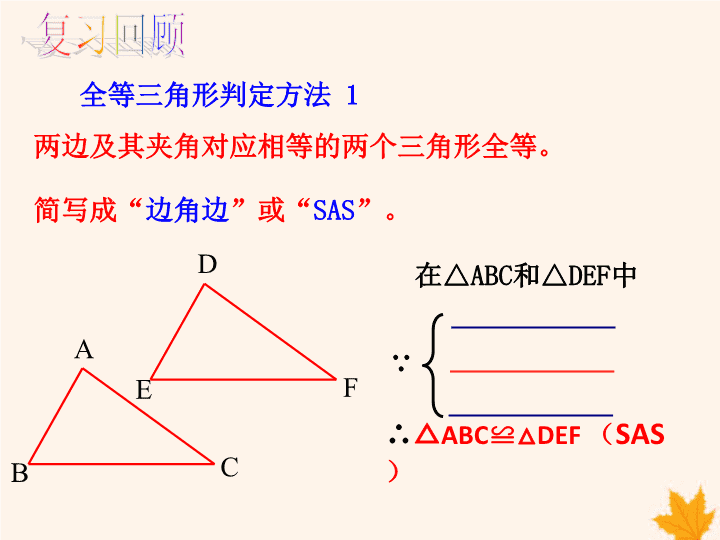
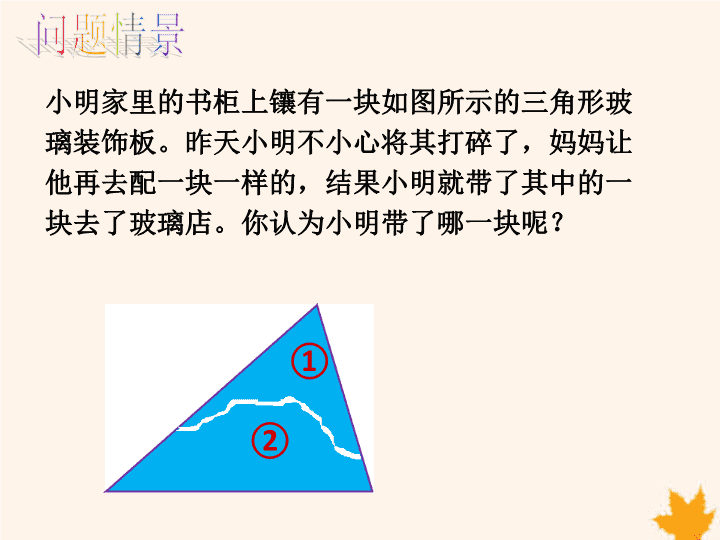
14.2 三角形全等的判定 第二课时 ASA 第十四章 A B C D E F 全等三角形判定方法 1 ∴△ABC≌△DEF (SAS) 两边及其夹角对应相等的两个三角形全等。 简写成“边角边”或“SAS”。 在△ABC和△DEF中 ∵ 小明家里的书柜上镶有一块如图所示的三角形玻 璃装饰板。昨天小明不小心将其打碎了,妈妈让 他再去配一块一样的,结果小明就带了其中的一 块去了玻璃店。你认为小明带了哪一块呢? ① ② 画线段AB=5cm , 再画∠BAP=45°, ∠ABQ=60°, AP与BQ相交于点C。 剪下所画的△ABC与 同桌进行比较。 A B PQ C 45° 60° 两角及其夹边对应相等的两个三 角形是否全等? 画一个△ABC,使得AB=5cm, ∠A=45°,∠B=60°. 5cm 你能得到什么结论? P A B Q C 45° 60° 两角及其夹边对应相等的两个三 角形是否全等? P A B Q C 45° 60° 5cm5cm 三角形全等判定方法 2 在△ABC与△DEF中 ∴ △ABC≌△DEF(ASA) 两角及其夹边对应相等的两个三角形全等。 简写成“角边角”或“ASA”。 ∠A=∠D AB=DE ∠B=∠E ∵ C A B 40° 60°cm5.4 D E F 40° 60°cm5.4 已知:如图,∠1=∠2,∠3=∠4.求证:DB=CB 证明:∵∠3 +∠5=180°,∠4 +∠6=180° ∴ ∠5=∠6(等角的补角相等) 在△ABD和△ABC中, ∴ △ABD ≌ △ABC ( ASA) B D A C P 1 2 3 45 6 (平角定义) 又∵∠3 =∠4 (已知) ∠1=∠2 ( 已知 ) AB=AB (公共边) ∠5=∠6 ( 已证 ) ∵ ∴ DB = CB (全等三角形对应边相等) 证明: 在△ABC和△BAD中 ∵ ∠DAB=∠CBA (已证) AB = BA (公共边) ∴△ABC≌△BAD ( ASA ) 1.已知:如图,∠1=∠2,∠3=∠4, 求证:△ABC≌△BAD. 1 2 43 ∵ ∠1=∠2,∠3=∠4(已知) 即 ∠DAB = ∠CBA ∠1 = ∠2 (已知) ∴ ∠1+∠3=∠2+∠4(等式性质) 2.已知:如图,在△ABC中, AD平分∠BAC,AD⊥BC于点D, 求证:∠B=∠C. 1 2 3 4 在△ABD和△ACD中 ∵ ∠3 = ∠4 (已证) AD = AD (公共边) ∴△ABD≌△ACD ( ASA ) ∵ AD平分∠BAC(已知) ∠1 = ∠2 (已证) 证明: ∴∠1=∠2 (角平分线定义) ∵ AD⊥BC(已知) ∴∠3=∠4=90° (垂直定义) ∴∠B =∠C (全等三角形对应角相等) 3.已知:如图,点A、B、C、D在同一条直线上, AB=CD,AE⊥AD于A,BF⊥AD于B,CE∥DF. 求证:AE=BF. 1 2 已知:如图,A、B、C、D四点在同一条直线上,AB=CD, AE⊥AD于A,BF⊥AD于B,CE∥DF.求证:AE=BF. 1 2 在△ACE和△BDF中 ∵ ∠2 = ∠D (已证) AC = BD (已证) ∴△ACE≌△BDF( ASA ) ∵ AE⊥AD,BF⊥AD(已知) ∠A = ∠1 (已证) 证明: ∵ CE∥DF(已知) ∴∠2=∠D ∴AE =BF (全等三角形对应边相等) ∴∠A=∠1=90°(垂直定义) ∵ AB=CD (已知) ∴ AB+BC=CD+BC(等式性质) 即 AC=BD 2.在应用“ASA”时要注意:必须是对应的两 角及两角所夹的边相等。 1.角边角:两角和它们的夹边对应相等的两个 三角形全等(ASA)。 3.今后判定两条线段相等或两个角相等可以通 过证明它们所在的两个三角形全等而得到。 本节课你有什么收获?查看更多