2021届高考数学一轮复习第二章函数概念及基本初等函数Ⅰ创新引领微课探秘基本初等函数的命题热点动向课件新人教A版

2021届高考数学一轮复习第二章函数概念及基本初等函数Ⅰ创新引领微课探秘基本初等函数的命题热点动向课件新人教A版

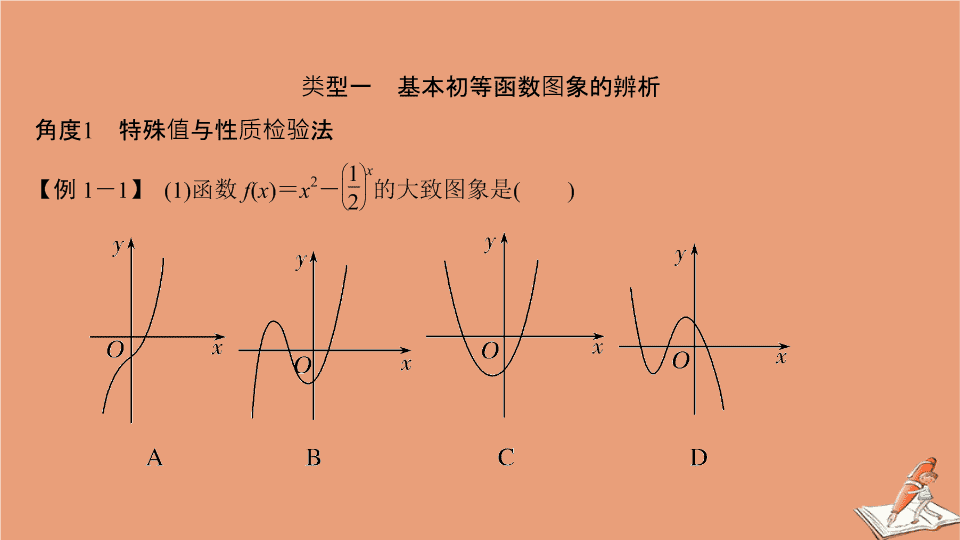
探秘基本初等函数的命题热点动向 微点聚焦突破 以二次函数、幂函数、指数与对数函数为载体考查函数图象与性质，灵活利用图象、性质解决与方程 ( 不等式 ) 的交汇融合问题，相关参数求解与讨论一直是命题的热点，常以客观题的形式呈现，考查学生数学运算、直观想象、逻辑推理数学核心素养 . 类型一　基本初等函数图象的辨析 角度 1 　特殊值与性质检验法 (2) (2019· 福州质检 ) 函数 f ( x ) ＝ x 2 ＋ ln(e － x )ln(e ＋ x ) 的大致图象为 ( 　　 ) 解析　 (1) 由 f (0) ＝－ 1 ，知图象过点 (0 ，－ 1) ，排除 D 项 . 又 f ( － 2) ＝ 4 － 4 ＝ 0 ， f ( － 4) ＝ 16 － 16 ＝ 0 ， ∴ f ( x ) 的图象过点 ( － 2 ， 0) ， ( － 4 ， 0) ，排除 A ， C ，只有 B 适合 . (2) 易知 f ( － x ) ＝ ( － x ) 2 ＋ ln(e ＋ x )ln(e － x ) ＝ x 2 ＋ ln(e － x )ln(e ＋ x ) ＝ f ( x ) ， ∴ y ＝ f ( x ) 的图象关于 y 轴对称，排除 C 项 . 又当 x → e 时， f ( x ) → － ∞ ，排除选项 B ， D. 答案　 (1)B 　 (2)A 思维升华　 1. 求解该类问题抓住两点： (1) 根据函数的奇偶性、周期性、单调性排除不符合的选项 .(2) 利用特殊值 ( 点 ) 或极限的思想，排除不可能选项 . 2. 注意两点： (1) 特殊点或特殊值要具备特殊性和代表性，只能否定错误的结论 . (2) 紧扣图象特征，揭示函数的性质 . 答案　 B 角度 2 　函数的图象变换法 【例 1 － 2 】 已知定义域为 R 的函数 f ( x ) 满足 f ( x ) ＝－ f ( x － 1) ，则函数 f ( x ) 在 ( － 1 ， 1] 上的图象可能是 ( 　　 ) 解析　 由 f ( x ) ＝－ f ( x － 1) 知，把 f ( x ) 在 ( － 1 ， 0) 上的图象向右平移一个单位长度，再把所得的图象关于 x 轴作对称变换，可以得到 y ＝ f ( x ) 在 (0 ， 1) 上的图象 . 结合图象特征， A ， B ， D 不满足，只有 C 符合 . 答案　 C 思维升华　 1. 通过图象变换识别函数图象要掌握两点：一是熟悉基本初等函数的图象 ( 如指数函数、对数函数等函数的图象 ) ；二是了解一些常见的变换形式，如平移变换、伸缩变换、翻折变换 . 2. 函数图象进行左右平移变换，一定是仅仅相对于 “ 自变量 x ” 而言的，一定把 x 的系数变为 1. 【训练 2 】 (2020· 武汉部分重点中学联考 ) 已知函数 y ＝ sin ax ＋ b ( a >0) 的图象，如图所示，则函数 y ＝ log a ( x ＋ b ) 的图象可能是 ( 　　 ) 解析　 由 y ＝ sin ax ＋ b 的图象知，周期 T >2π ， 0< b <1. ∴ y ＝ log a ( x ＋ b ) 在 ( － b ，＋ ∞ ) 上是减函数，排除 B ， D. 把 y ＝ log a x 的图象向左平移 b 个单位长度， 得 y ＝ log a ( x ＋ b ) 的图象，排除 C 项，只有 A 符合 . 答案　 A 类型二　基本初等函数的性质应用 角度 1 　比较数值的大小 【例 2 － 1 】 (2020· 青岛二中检测 ) 设 x ， y ， z 为正实数，且 log 2 x ＝ log 3 y ＝ log 5 z >0 ，则下列关系式不可能成立的是 ( 　　 ) 解析　 令 log 2 x ＝ log 3 y ＝ log 5 z ＝ k >0 ， 则 x ＝ 2 k >1 ， y ＝ 3 k >1 ， z ＝ 5 k >1 ， 若 k >1 时，则 f ( x ) ＝ x k － 1 在 (0 ，＋ ∞ ) 上单调递增， 综上，选项 A ， B ， D 都有可能成立，只有 C 不成立 . 答案　 C 思维升华　 1. 本题考查对数定义，幂函数、指数函数的单调性及应用，着重考查逻辑推理、数学运算等数学核心素养 . 2. 运用基本初等函数性质求解问题，要注意不同参数取值对性质的影响，必要时要进行分类讨论 . A. f ( a )> f ( b )> f ( c ) B. f ( b )> f ( c )> f ( a ) C. f ( c )> f ( b )> f ( a ) D. f ( c )> f ( a )> f ( b ) 答案　 D 角度 2 　利用性质求函数值或范围 解析　 (1) 由 g ( x ＋ 2) ＝－ g ( x ) ，得 g ( x ＋ 4) ＝ g ( x ) ， ∴ 4 是函数 g ( x ) 的周期 . 则 g ( － 2 021) ＝ g ( － 505 × 4 － 1) ＝ g ( － 1). 又 f ( x ) 在 ( － 2 ， 0) ∪ (0 ， 2) 上是偶函数， ∴ g ( － 1) ＝ f ( － 1) ＝ f (1) ＝ log 2 1 ＝ 0. 思维升华　 破解此类题的关键：一是活用函数的性质，如周期性、奇偶性；二是利用转化思想，把原不等式转化为关于自变量的不等式组，解不等式组，即可得自变量的取值范围 . 若能灵活应用特值法，则可加快解题的速度 . 解析　 当 x >0 时， f ( x ) ＝ 2 x － 2 － x 是增函数； 当 x ≤ 0 时， f ( x ) ＝ 0. 类型三　运用基本初等函数图象性质解零点问题 又当 x → － ∞ 时， f ( x ) → － ∞ ；当 x → ＋ ∞ 时， f ( x ) → 0 且 f ( x )>0 ， 又 f (0) ＝ 0 ，从而作出 t ＝ f ( x ) 的简图，如图所示 . 令 t ＝ f ( x ) ， g ( t ) ＝ t 2 ＋ mt ＋ m － 1. 由 g ( t ) ＝ 0 ，得 t ＝－ 1 或 t ＝ 1 － m . 要使原方程有 3 个不同的实数解，必须 t ＝ 1 － m 与 t ＝ f ( x ) 的图象有两个交点 . 思维升华　 1. 题目以函数的图象、性质为载体，考查函数零点 ( 方程的根 ) 中参数的求解，综合考查直观想象、数学运算、逻辑推理等数学核心素养 . 2. 涉及复合函数零点的步骤： ① 换元，令 t ＝ f ( x ) ， y ＝ g ( t ) ， f ( x ) 为 “ 内函数 ” ， g ( t ) 为 “ 外函数 ” ； ② 作图，作 “ 外函数 ” y ＝ g ( t ) 的图象与 “ 内函数 ” t ＝ f ( x ) 的图象； ③ 观察图象进行分析 . 解析　 作出函数 f ( x ) 的图象如图所示， 不妨设 a < b < c < d ，则－ log 2 a ＝ log 2 b ， ∴ ab ＝ 1. 又根据二次函数的对称性，可知 c ＋ d ＝ 7 ， ∴ 10< cd <12 ， ∴ abcd 的取值范围是 (10 ， 12). 答案　 (10 ， 12)