- 2021-05-26 发布 |
- 37.5 KB |
- 19页
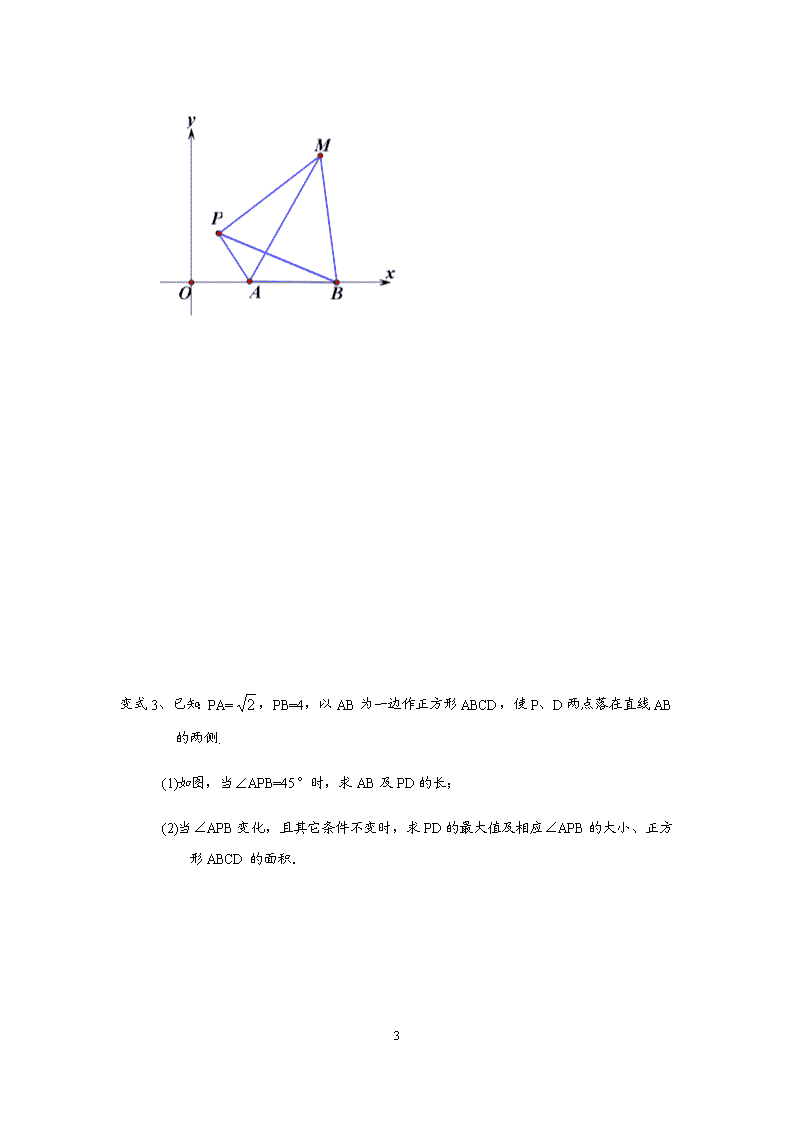
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学复习 瓜豆原理 ——旋转相似之主动从动
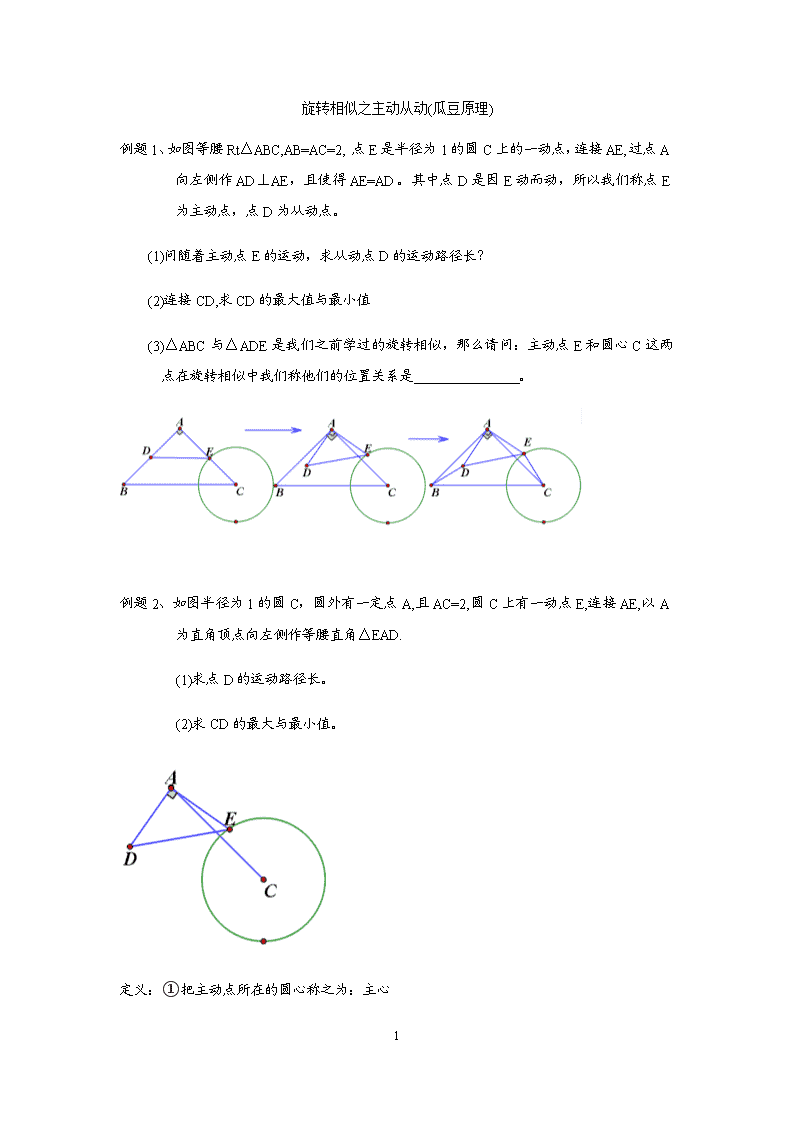
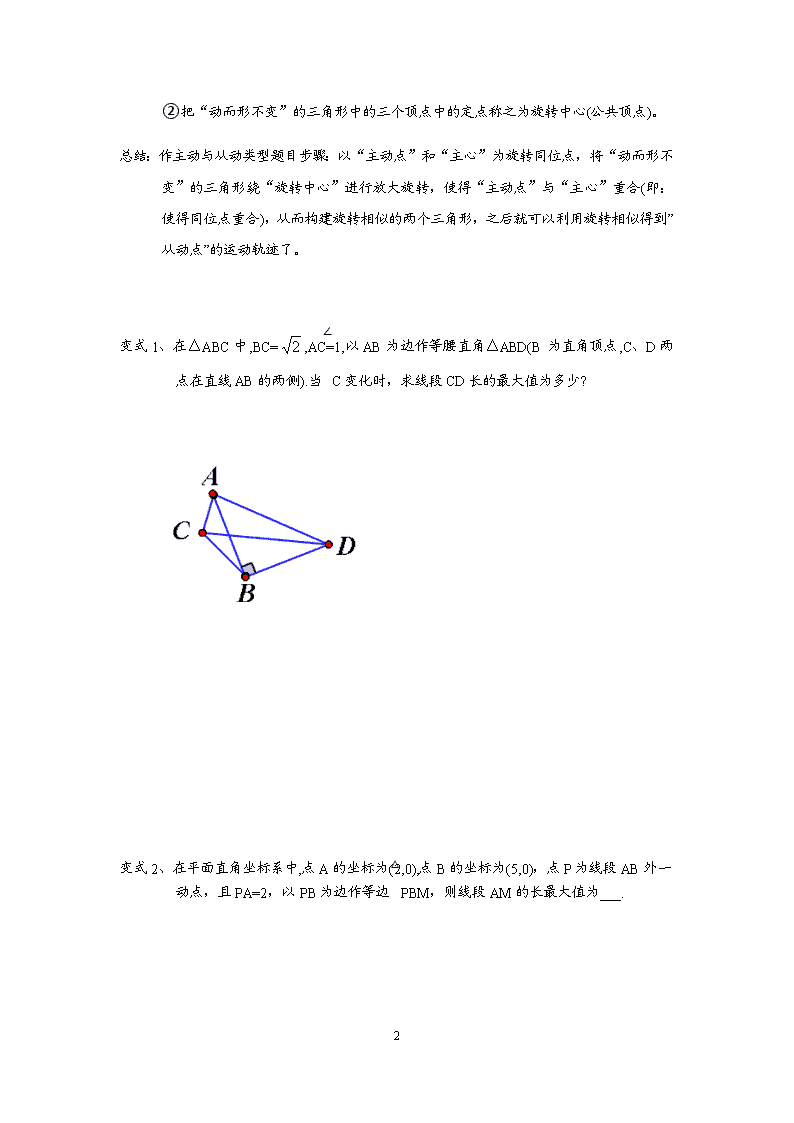
1 旋转相似之主动从动(瓜豆原理) 例题 1、如图等腰 Rt△ABC,AB=AC=2,点 E 是半径为 1 的圆 C 上的一动点,连接 AE,过点 A 向左侧作 AD⊥AE,且使得 AE=AD。其中点 D 是因 E 动而动,所以我们称点 E 为主动点,点 D 为从动点。 (1)问随着主动点 E 的运动,求从动点 D 的运动路径长? (2)连接 CD,求 CD 的最大值与最小值 (3)△ABC 与△ADE 是我们之前学过的旋转相似,那么请问:主动点 E 和圆心 C 这两 点在旋转相似中我们称他们的位置关系是 。 例题 2、如图半径为 1 的圆 C,圆外有一定点 A,且 AC=2,圆 C 上有一动点 E,连接 AE,以 A 为直角顶点向左侧作等腰直角△EAD. (1)求点 D 的运动路径长。 (2)求 CD 的最大与最小值。 定义:①把主动点所在的圆心称之为:主心 2 ②把“动而形不变”的三角形中的三个顶点中的定点称之为旋转中心(公共顶点)。 总结:作主动与从动类型题目步骤:以“主动点”和“主心”为旋转同位点,将“动而形不 变”的三角形绕“旋转中心”进行放大旋转,使得“主动点”与“主心”重合(即: 使得同位点重合),从而构建旋转相似的两个三角形,之后就可以利用旋转相似得到” 从动点”的运动轨迹了。 变式 1、在△ABC 中,BC= 2 ,AC=1,以 AB 为边作等腰直角△ABD(B 为直角顶点,C、D 两 点在直线 AB 的两侧).当∠C 变化时,求线段 CD 长的最大值为多少? 变式 2、在平面直角坐标系中,点 A 的坐标为(2,0),点 B 的坐标为(5,0),点 P 为线段 AB 外一 动点,且 PA=2,以 PB 为边作等边△PBM,则线段 AM 的长最大值为___. 3 变式 3、已知:PA= 2 ,PB=4,以 AB 为一边作正方形 ABCD,使 P、D 两点落在直线 AB 的两侧. (1)如图,当∠APB=45°时,求 AB 及 PD 的长; (2)当∠APB 变化,且其它条件不变时,求 PD 的最大值及相应∠APB 的大小、正方 形 ABCD 的面积. 4 变式 4、△ABC 中,AB=4,AC=2,以 BC 为边在△ABC 外作正方形 BCDE,BD、CE 交于点 O,则线段 AO 的最大值为 . 5 例题 3、如图,点 O 在线段 AB 上,OA=1,OB=3,以 O 为圆心,OA 为半径作圆 O,点 M 在圆 O 上运动,连接 MB,以 MB 为腰作等腰 Rt△ABC,使∠MBC=90°,M,B, C 三点按逆时针顺序排列,连接 AC,则 AC 长的取值范围是_____. 变式 1、如图,P 是圆 O 上一个动点,A 是圆 O 外的的一个定点,且 AO=4,连接 AP,作 AQ⊥AP,且 AQ=AP。若圆 O 的半径为 1,则当点 P 在圆 O 上运动时,求 OQ 的 最值. 6 变式 2、如图,点 P 是半径为 1 的圆 O 上的一个动点,点 A 是圆外的一个定点,且 OA=3, 连接 AP,以 AP 为边作等边三角形 APQ,随着点 P 运动的过程中,求 OQ 的最值 变式 3、如图,点 P 是半径为 1 的圆 O 上的一个动点,点 A 是圆外的一个定点,且 OA= 12 , 连接 AP,以 AP 为斜边作等腰直角三角形 APQ,当点 P 绕着点 O 运动一周后,求点 Q 的运动路径长. 7 变式 4、已知⊙O 的半径为 2,A 为圆上一定点,P 为圆上一动点,以 AP 为边作等腰 Rt△ APG,P 点在圆上运动一周的过程中,OG 的最大值为_____. 变式 5、如图,已知 A、C 是半径为 2 的⊙O 上的两动点,以 AC 为直角边在⊙O 内作等腰 Rt△ABC,∠C=90°.连接 OB.求 OB 的最值. 8 变式 6、已知⊙O 的半径为 2,A 为圆内一定点,AO=1.P 为圆上一动点,以 AP 为边作等 腰△APG,AP=PG,∠APG=120°,OG 的最大值为 . 变式 7、(2018·南通市)如图,正方形 ABCD 中,AB=2 5 ,O 是 BC 边的中点,点 E 是 正方形内一动点,OE=2,连接 DE,将线段 DE 绕点 D 逆时针旋转 90°得 DF, 连接 AE,CF. (1)求证:AE=CF. (2)若 A,E,O 三点共线,连接 OF,求线段 OF 的长. (3)求线段 OF 长的最小值. 9 A B C D A B CO E D F 变式 8、如图,线段 PA=3,点 B 是线段 PA 外一点,PB=5,连接 AB,将 AB 绕点 A 逆时针旋转 90° 得到线段 AC,随着点 B 的位置的变化,直接写出 PC 的范围。 10 变式 9、如图,已知圆 O 的半径为 2,A 是圆上一定点,B 是 OA 的中点,E 是圆上一动点, 以 BE 为边作正方形 BEFG(B、E、F、G 四点按逆时针顺序排列),当点 E 绕⊙O 圆 周旋转时,点 F 的运动轨迹围成的图形的面积是 。 变式 10、如图,已知在平面直角坐标系中,⊙O 的半径为 2,点 A 是⊙O 上一动点,点 B 是反比例函数 xy 4 (x>0)图象上一动点,以 AB 为斜边作等腰直角△ABC,连 结 OC,则 OC 的最小值为 . 11 变式 11、如图,正方形 ABCD 中,AB=3cm,以 B 为圆心,1cm 长为半径画 B,点 P 在 B 上移动, 连接 AP,并将 AP 绕点 A 逆时针旋转 90°至 AP′,连接 BP′.在点 P 移动的过程中,BP′ 长度的最小值为___cm. 变式 12、如图,已知扇形 AOB 中 OA=3,∠AOB=120。C 是弧 AB 上的动点,以 BC 为边向 右上方作正方形 BCDE.当点 C 从点 A 移动至点 B 时,求点 D 经过的路径长。 12 变式 13、在平面直角坐标系中,点 A 的坐标为(2,0)点 B 的坐标为(5,0),点 P 为线段 AB 外一动点,且 PA=2,PM=PB,∠BPM=90°,求线段 AM 的最大值及此时点 P 的坐标。 变式 14、如图,线段 AB,M 为 AB 的中点,动点 P 到点 M 的距离是 1,连接 PB,线段 PB 绕点 P 逆时针旋转 90°得到线段 PC,连接 AC,则线段 AC 长度的最大值是____ 13 旋转相似之构建相似三角形 例题 4、如图点 P 在半径为 2 的圆 O 上运动,点 A 是圆 O 外的一个定点,且 AO=6,连接 AP,过点 A 向上作 AQ⊥AP,且 AQ:AP=1:2。 ①问当点 P 绕点 O 运动一圈后,求点 Q 的运动轨迹长。 ②问在点 P 运动过程中,求 OQ 的最值。 14 变式 1、如图点 P 在半径为 2 的圆 O 上运动,点 A 是圆 O 外的一个定点,且 AO=6,连接 AP,过点 A 向上作 AQ⊥AP,且 tan∠QPA= 5 5 。 ①问当点 P 绕点 O 运动一圈后,求点 Q 的运动轨迹长。 ②问在点 P 运动过程中,求 OQ 的最值。 15 变式 2、如图,点 O 在线段 AB 上,OA=1,OB=2,以 O 为圆心,OA 为半径作⊙O,点 M 在⊙O 上运动,连接 MB,以 MB 为直角边作 Rt△ABC,使∠MBC=90°,且 tan ∠MCB= 2 1 ,M,B,C 三点按逆时针顺序排列,连接 AC,则 AC 长的取值范围是_____. 变式 3、(1)如图 1,在△ACB=90°,CH⊥AB 于点 H,若 AB=6,则 CH 的最大值为 。 (2)如图 2,在四边形 ABCD 中,AB=12,BC=CD,∠BCD=60°,AD=9,连接 AC,求 △ABC 面积的最大值。 (3)如图 3.某市郊区点 O 处有棵古树,点 A 处是某市古树名木保护研究中心,且 16 OA=40km.为加强对该古树的检测和保护.拟在距古树 3km 处设置三个观测点 B, C,D.以形成保护区域四边形 ABCD.那么,是否可以形成一个满足要求的面积最 大的四边形 ABCD?若可以,求出满足条件的四边形 ABCD 的最大面枳;若不可 以,并说明理由.(研究中心及各观测点的占地面枳爸略不计) 构建旋转全等进行边的转换 【条件】 CODAOBODOCOBOA ,, 将△OCD 绕点 O 旋转。 【1】求证:△OAC≌△OBD; 【2】若 AC=3,求 BD 的长。 17 例题 1.1、如图,在四边形 ABCD 中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,求 BD 的长. 变式 1、如图,点 A 是△DBC 内一点,AB= 32 ,BC=8,∠DAC=120°,∠ABC=60°, AD=AC,求 BD 的长。 变式 2、①如左图,四边形 ABCD 中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45∘ ,求 BD 的长。 18 ②如右图,在①的条件下,当△ACD 在线段 AC 的左侧时,求 BD 的长。 变式 3、如图,四边形 ABCD 中,∠CAB=90°,∠ADC=∠ACB=α,tanα=43,CD=5,AD=12, 求 BD 的长。 19 变式 4、如图,在四边形 ABCD 中,BC=5,CD=8,AB=AC= AD2 1 ,∠BAC=2∠ADC,请直接写 出 BD 的长。查看更多