人教版初中数学八年级下册课件19.1.2 函数的图象第2课时 函数的表示方法

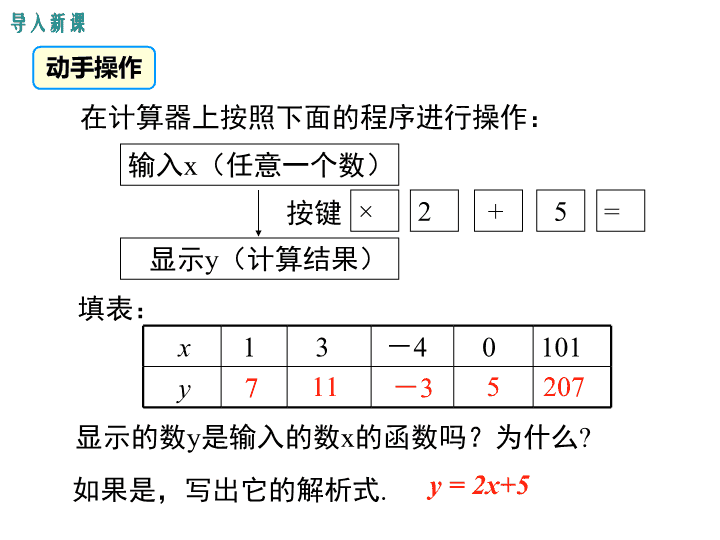
人教版初中数学八年级下册课件19.1.2 函数的图象第2课时 函数的表示方法

导入新课 讲授新课 当堂练习 课堂小结 19.1.2 函数的图象 第十九章 一次函数 第2课时 函数的表示方法 情境引入 学习目标 1．了解函数的三种表示方法及其优点； 2．能用适当的方式表示简单实际问题中的变量之间 的函数关系；(重点） 3．能对函数关系进行分析，对变量的变化情况进行 初步讨论.（难点） 在计算器上按照下面的程序进行操作： 输入x（任意一个数） 按键 × 2 = 显示y（计算结果） 　x 1 3 －4 0 101 　y 7 11 －3 5 207 显示的数y是输入的数x的函数吗？为什么? 填表： + 5 如果是，写出它的解析式. y = 2x+5 导入新课 动手操作 讲授新课 函数的三种表示方法 用平面直角坐标系中的 一个图象来表示的． 问题1.下图是某地气象站用自动温度记录仪描出的 某一天的温度曲线，气温T是不是时间t 的函数？ 这里是怎样表示气温T 与时间t之间的函数关 系的？ 是 合作探究 问题2.正方形的面积S与边长x的取值如下表， 面积S是不是边长x的函数？ 这里是怎样表示正方形面积S与边长x之间的 函数关系的？ 列表格来表示的． 1 4 9 16 25 36 49 是 问题3.某城市居民用的天然气，１m3收费2.88元， 使用x（m3） 天然气应缴纳的费用y（元）为y = 2.88x． y是不是x 的函数？ 这里是怎样表示缴纳的天然气费y与所用天 然气的体积x的函数关系的？ 用函数解析式y＝2.88x来表示． 是 函数的三种表示法： y = 2.88x 图象法、列表法、解析式法． 1 4 9 16 25 36 49 知识要点 1.解析式法：准确地反映了函数与自变量之间的数 量关系. 2.列表法：具体地反映了函数与自变量的数值对应 关系. 3.图象法：直观地反映了函数随自变量的变化而变 化的规律. 议一议 这三种表示函数的方法各有什么优点？ 　例 1.如图，要做一个面积为12 m2的小花坛，该花 坛的一边长为 x m，周长为 y m． 　 （1）变量 y 是变量 x 的函数吗？如果是，写出自 变量的取值范围； 　 （2）能求出这个问题的函数解析式吗？ x 解：（1）y 是 x 的函数，自变量 x 的取值范围是x＞ 0． 　（2）y =2（x +　 ）　 12 x 典例精析 　 （3）当 x 的值分别为1，2，3，4，5，6 时，请 列表表示变量之间的对应关系； 　 （4）能画出函数的图象吗？ x/m 1 2 3 4 5 6 y/m 26 16 14 14 14.8 16 40 35 30 25 20 15 10 5 5 10O x y （3） 已知等腰三角形的面积为30cm2，设它的底边 长为xcm，底边上的高为ycm (1)求底边上的高y随底边长x变化的函数解析 式．并求自变量的取值范围． (2)当底边长为10cm时,底边上的高是多少cm? 解： x＞0 (2)当x=10时，y=60÷10=6 x y 60=(1) 做一做 　例 2.一水库的水位在最近5 h 内持续上涨，下表记录 了这5 h 内6 个时间点的水位高度，其中 t 表示时间，y 表示水位高度． 　 （1）在平面直角坐标系中描出表中数据对应的点， 这些点是否在一条直线上？由此你发现水位变化有什 么规律？ t/h 0 1 2 3 4 5 y/m 3 3.3 3.6 3.9 4.2 4.5 x/h y/m O 1 2 3 4 5 6 7 8 1 2 3 4 解：可以看出，这6个点 ，且每 小时水位 .由此猜想，在这个时间 段中水位可能是以同一速度均匀上升的. 在同一直线上 上升0.3m 5 （2）水位高度 y 是否为时间 t 的函数？如果是，试写 出一个符合表中数据的函数解析式，并画出函数图象． 这个函数能表示水位的变化规律吗？ （2）由于水位在最近5小时内持续上涨，对于时间t 的每一个确定的值，水位高度y 都有 的值 与其对应，所以，y t 的函数. 函数解析式为： . 自变量的取值范围是： . 它表示在这 小 时内，水位匀速上升的速度为 ，这个函数 可以近似地表示水位的变化规律. 唯一 是 y=0.3t+3 0≤t≤5 5 0.3m/h （3）据估计这种上涨规律还会持续2 h，预测 再过2 h水位高度将达到多少m． （3）如果水位的变化规律不变，按上述函数预测， 再持续2小时，水位的高度： . 此时函数图象（线段AB）向 延伸到对应的 位置，这时水位高度约为 m. 5.1m 右 5.1 已知火车站托运行李的费用C（元）和托运行李的 重量P（千克）（P为整数）的对应关系如表： 做一做 P 1 2 3 4 5 … C 2 2.5 3 3.5 4 … （1）已知小周的所要托运的行李重12千克，请问小 周托运行李的费用为多少元？ （2）写出C与P之间的函数解析式. （3）小李托运行李花了15元钱，请问小李的行李重 多少千克？ 7.5元 C=0.5P+1.5 27千克 1. 小明所在学校与家距离为2千米，某天他放学后骑自 行车回家，行驶了5分钟后，因故停留10分钟，继续骑 了5分钟到家.如图，能大致描述他回家过程中离家的距 离s(千米)与所用时间t(分)之间的关系图象的是（ ） 当堂练习 D 2.某工厂投入生产一种机器，每台成本y（万元/ 台）与生产数量x（台）之间是函数关系，函数y 与自变量x的部分对应值如下表： x（单位：台） 10 20 30 y（单位：万元/台） 60 55 50 C则y与x之间的解析式是（ ） A.y=80- 2x B.y=40+ 2x C. y=65- x 2 1 D.y=60- x 2 1 3.用列表法与解析式法表示n边形的内角和m（单 位：度）是边数n的函数. 解：因为n表示的是多边形的边数，所以n是大于 等于3的自然数，列表如下： n 3 4 5 6 … m … 所以m=（n-2）·180°（n≥3，且n为自然数）. 180 360 540 720 提示：n边形的内角和公式是:(n-2) ×180°. 4.用解析式法与图象法表示等边三角形的周长l是 边长a的函数. a … 1 2 3 4 … l … 3 6 9 12 … 描点、连线： 用描点法画函数l=3a的图象. O 2 x y 1 2 3 4 5 8 6 4 10 12 解：因为等边三角形的周长l是边长a的3倍，所 以周长l与边长a的函数关系可表示为l=3a（a＞0）. 5.一条小船沿直线向码头匀速前进.在0min ，2min， 4min，6min时，测得小船与码头的距离分别为200m， 150m，100m，50m. （1）小船与码头的距离是时间的函数吗？ （2）如果是，写出函数的解析式，并画出函数图象. 函数解析式为： . 列表： t/min 0 2 4 6 …… s/m 200 150 100 50 …… 是 s = 200-25t 船速度为（200-150） ÷2=25m/min， s=200-25t t/min s/m O 1 2 3 4 5 6 7 50 100 150 200 画图： 课堂小结 函数的表 示方法 解析式法：反映了函数与 自变量之间的数量关系 列表法：反映了函数与自 变量的数值对应关系 图象法：反映了函数随自 变量的变化而变化的规律