【数学】2019届一轮复习北师大版(文科数学)第三章第2讲 导数与函数的单调性学案
第2讲 导数与函数的单调性
函数的单调性与导数的关系
条件
结论
函数y=f(x)在区间(a,b)上可导
f′(x)>0
f(x)在(a,b)内单调递增
f′(x)<0
f(x)在(a,b)内单调递减
f′(x)=0
f(x)在(a,b)内是常数函数
判断正误(正确的打“√”错误的打“×”)
(1)若函数f(x)在(a,b)内单调递增,那么一定有f′(x)>0.( )
(2)如果函数f(x)在某个区间内恒有f′(x)=0,则f(x)在此区间内没有单调性.( )
(3)在(a,b)内f′(x)≤0且f′(x)=0的根有有限个,则f(x)在(a,b)内是减函数.( )
答案:(1)× (2)√ (3)√
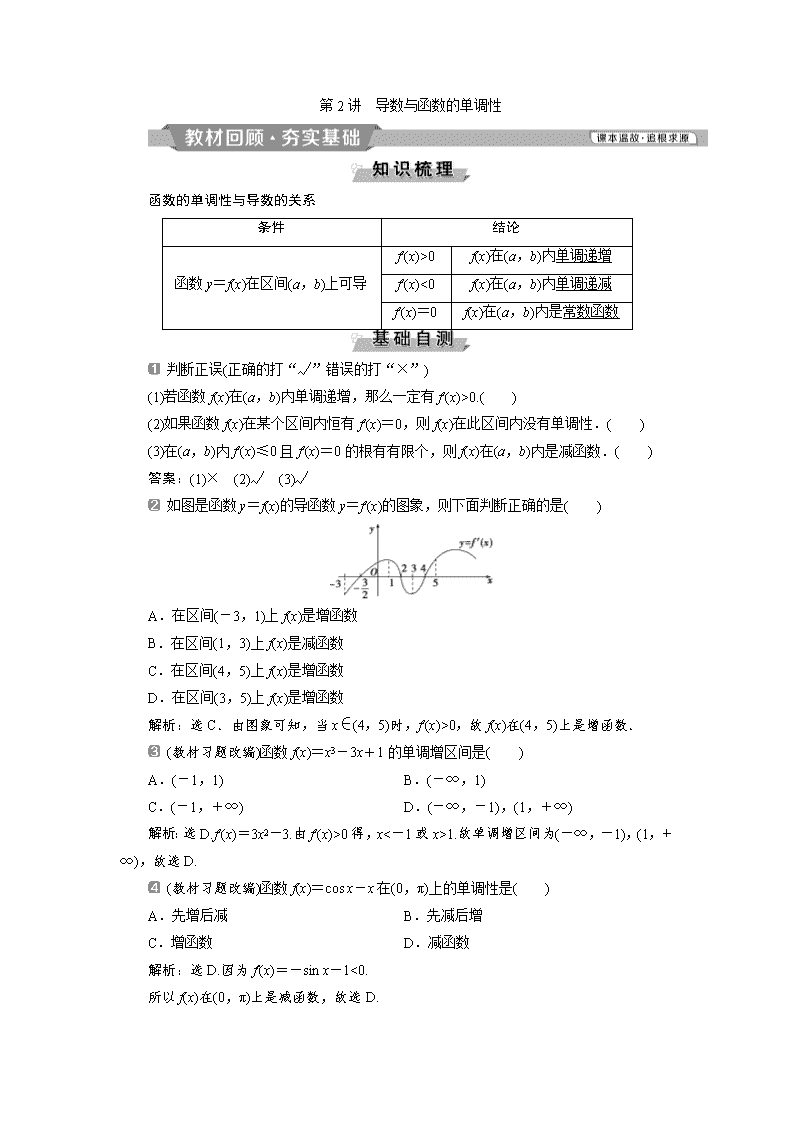
如图是函数y=f(x)的导函数y=f′(x)的图象,则下面判断正确的是( )
A.在区间(-3,1)上f(x)是增函数
B.在区间(1,3)上f(x)是减函数
C.在区间(4,5)上f(x)是增函数
D.在区间(3,5)上f(x)是增函数
解析:选C.由图象可知,当x∈(4,5)时,f′(x)>0,故f(x)在(4,5)上是增函数.
(教材习题改编)函数f(x)=x3-3x+1的单调增区间是( )
A.(-1,1) B.(-∞,1)
C.(-1,+∞) D.(-∞,-1),(1,+∞)
解析:选D.f′(x)=3x2-3.由f′(x)>0得,x<-1或x>1.故单调增区间为(-∞,-1),(1,+∞),故选D.
(教材习题改编)函数f(x)=cos x-x在(0,π)上的单调性是( )
A.先增后减 B.先减后增
C.增函数 D.减函数
解析:选D.因为f′(x)=-sin x-1<0.
所以f(x)在(0,π)上是减函数,故选D.
函数f(x)=x-ln x的单调递减区间为( )
A.(0,1) B.(0,+∞)
C.(1,+∞) D.(-∞,0)∪(1,+∞)
解析:选A.由f′(x)=1-<0,得>1,
即x<1,又x>0,
所以函数f(x)的单调递减区间为(0,1).
(教材习题改编)函数f(x)=sin x+kx在(0,π)上是增函数,则实数k的取值范围为________.
解析:因为f′(x)=cos x+k≥0,
所以k≥-cos x,x∈(0,π)恒成立.
当x∈(0,π)时,-1<-cos x<1,
所以k≥1.
答案:k≥1
不含参数的函数的单调性
[典例引领]
(1)函数y=x2-ln x的单调递减区间为( )
A.(-1,1) B.(0,1)
C.(1,+∞) D.(0,+∞)
(2)已知定义在区间(-π,π)上的函数f(x)=xsin x+cos x,则f(x)的单调递增区间是________.
【解析】 (1)y=x2-ln x,
y′=x-==(x>0).
令y′<0,得0
0,
则其在区间(-π,π)上的解集为和,
即f(x)的单调递增区间为和.
【答案】 (1)B (2)和
求函数单调区间的步骤
(1)确定函数f(x)的定义域;
(2)求f′(x);
(3)在定义域内解不等式f′(x)>0,得单调递增区间;
(4)在定义域内解不等式f′(x)<0,得单调递减区间.
[注意] (1)求函数的单调区间时,一定要先确定函数的定义域,否则极易出错.
(2)个别导数为0的点不影响所在区间的单调性,如函数f(x)=x3,f′(x)=3x2≥0(x=0时,f′(x)=0),但f(x)=x3在R上是增函数.
[通关练习]
1.函数y=4x2+的单调增区间为( )
A.(0,+∞) B.(,+∞)
C.(-∞,-1) D.
解析:选B.由y=4x2+,得y′=8x-,
令y′>0,即8x->0,解得x>,
所以函数y=4x2+的单调增区间为.
故选B.
2.已知函数f(x)=xln x,则f(x)( )
A.在(0,+∞)上递增 B.在(0,+∞)上递减
C.在(0,)上递增 D.在上递减
解析:选D.因为函数f(x)=xln x,定义域为(0,+∞),所以f′(x)=ln x+1(x>0),
当f′(x)>0时,解得x>,
即函数的单调递增区间为(,+∞);
当f′(x)<0时,解得00,故f(x)在(0,+∞)上单调递增;
②当a≤0时,f′(x)<0,故f(x)在(0,+∞)上单调递减;
③当00,
故f(x)在(0, )上单调递减,在( ,+∞)上单调递增.
解决含参数的函数单调性问题应注意2点
(1)研究含参数的函数的单调性,要依据参数对不等式解集的影响进行分类讨论.
(2)划分函数的单调区间时,要在函数定义域内讨论,还要确定导数为0的点和函数的间断点.
[通关练习]
已知函数f(x)=x3+x2+ax+1(a∈R),求函数f(x)的单调区间.
解:f′(x)=x2+2x+a开口向上,Δ=4-4a=4(1-a).
①当1-a≤0,即a≥1时,f′(x)≥0恒成立,
f(x)在R上单调递增.
②当1-a>0,即a<1时,令f′(x)=0,
解得x1==-1-,x2=-1+,
令f′(x)>0,解得x<-1-或x>-1+;
令f′(x)<0,解得-1--有解.
设G(x)=-,
所以只要a>G(x)min即可.
而G(x)=(-1)2-1,
所以G(x)min=-1.
所以a>-1.
(2)由h(x)在[1,4]上单调递减得,
当x∈[1,4]时,h′(x)=-ax-2≤0恒成立,
即a≥-恒成立.
所以a≥G(x)max,而G(x)=(-1)2-1,
因为x∈[1,4],所以∈[,1],
所以G(x)max=-(此时x=4),
所以a≥-,即a的取值范围是[-,+∞).
根据函数单调性求参数的一般思路
(1)利用集合间的包含关系处理:y=f(x)在(a,b)上单调,则区间(a,b)是相应单调区间的子集.
(2)f(x)为增函数的充要条件是对任意的x∈(a,b)都有f′(x)≥0且在(a,b)内的任一非空子区间上f′(x)不恒为零,应注意此时式子中的等号不能省略,否则漏解.
(3)函数在某个区间存在单调区间可转化为不等式有解问题.
[注意] (1)注意利用分离参数法或函数的性质求解恒成立问题.
(2)对等号单独检验,检验参数的取值能否使f′(x)在整个区间恒等于0,若f′(x)恒等于0,则参数的这个值应舍去;若只有在个别点处有f′(x)=0,则参数可取这个值.
[通关练习]
已知函数f(x)=x3-ax-1.
(1)若f(x)在R上为增函数,求实数a的取值范围;
(2)若函数f(x)在(-1,1)上为单调减函数,求实数a的取值范围;
(3)若函数f(x)的单调递减区间为(-1,1),求实数a的值;
(4)若函数f(x)在区间(-1,1)上不单调,求实数a的取值范围.
解:(1)因为f(x)在(-∞,+∞)上是增函数,
所以f′(x)=3x2-a≥0在(-∞,+∞)上恒成立,
即a≤3x2对x∈R恒成立.
因为3x2≥0,
所以只需a≤0.
又因为a=0时,f′(x)=3x2≥0,
f(x)=x3-1在R上是增函数,所以a≤0,即实数a的取值范围为(-∞,0].
(2)由题意知f′(x)=3x2-a≤0在(-1,1)上恒成立,
所以a≥3x2在(-1,1)上恒成立,
因为当-10.
令f′(x)=0,解得x=±.
因为f(x)在区间(-1,1)上不单调,所以f′(x)=0在(-1,1)上有解,需0<<1,得00,f′(x)<0的解,并注意函数f(x)的定义域.
(2)含参函数的单调性要分类讨论,通过确定导数的符号判断函数的单调性.
(3)已知函数单调性可以利用已知区间和函数单调区间的包含关系或转化为恒成立问题两种思路解决.
利用导数研究函数的单调性应注意4点
(1)求单调区间应遵循定义域优先的原则.
(2)注意两种表述“函数f(x)在(a,b)上为减函数”与“函数f(x)的减区间为(a,b)”的区别.
(3)在某区间内f′(x)>0(f′(x)<0)是函数f(x)在此区间上为增(减)函数的充分不必要条件.
(4)可导函数f(x)在(a,b)上是增(减)函数的充要条件是:对∀x∈(a,b),都有f′(x)≥0(f′(x)≤0),且f′(x)在(a,b)的任何子区间内都不恒为零.
1.函数f(x)=ex-ex,x∈R的单调递增区间是( )
A.(0,+∞) B.(-∞,0)
C.(-∞,1) D.(1,+∞)
解析:选D.由题意知,f′(x)=ex-e,令f′(x)>0,解得x>1,故选D.
2.函数f(x)的导函数f′(x)有下列信息:
①f′(x)>0时,-1<x<2;
②f′(x)<0时,x<-1或x>2;
③f′(x)=0时,x=-1或x=2.
则函数f(x)的大致图象是( )
解析:选C.根据信息知,函数f(x)在(-1,2)上是增函数.在(-∞,-1),(2,+∞)上是减函数,故选C.
3.若函数f(x)=kx-ln x在区间(1,+∞)上单调递增,则k的取值范围是( )
A.(-∞,-2] B.(-∞,-1]
C.[2,+∞) D.[1,+∞)
解析:选D.由于f′(x)=k-,f(x)=kx-ln x在区间(1,+∞)上单调递增⇔f′(x)=k-≥
0在(1,+∞)上恒成立.由于k≥,而0<<1,所以k≥1.即k的取值范围为[1,+∞).
4.已知函数f(x)=xsin x,x∈R,则f,f(1),f的大小关系为( )
A.f>f(1)>f B.f(1)>f>f
C.f>f(1)>f D.f>f>f(1)
解析:选A.因为f(x)=xsin x,
所以f(-x)=(-x)sin(-x)=xsin x=f(x).
所以函数f(x)是偶函数,所以f=f.
又x∈时,得f′(x)=sin x+xcos x>0,所以此时函数是增函数.
所以ff(1)>f,故选A.
5.函数f(x)的定义域为R.f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
A.(-1,1) B.(-1,+∞)
C.(-∞,-1) D.(-∞,+∞)
解析:选B.由f(x)>2x+4,得f(x)-2x-4>0.设F(x)=f(x)-2x-4,则F′(x)=f′(x)-2.
因为f′(x)>2,所以F′(x)>0在R上恒成立,所以F(x)在R上单调递增,而F(-1)=f(-1)-2×(-1)-4=2+2-4=0,故不等式f(x)-2x-4>0等价于F(x)>F(-1),所以x>-1,选B.
6.若函数f(x)=ax3+3x2-x恰好有三个单调区间,则实数a的取值范围是________.
解析:由题意知f′(x)=3ax2+6x-1,由函数f(x)恰好有三个单调区间,得f′(x)有两个不相等的零点,所以3ax2+6x-1=0需满足a≠0,且Δ=36+12a>0,解得a>-3,所以实数a的取值范围是(-3,0)∪(0,+∞).
答案:(-3,0)∪(0,+∞)
7.(2018·张掖第一次诊断考试)若函数f(x)=-x2+x+1在区间上单调递减,则实数a的取值范围是________.
解析:f′(x)=x2-ax+1,因为函数f(x)在区间(,3)上单调递减,所以f′(x)≤0在区间(,3)上恒成立,所以,即,解得a≥,所以实数a的取值范围为[
eq f(10,3),+∞).
答案:[,+∞)
8.(2017·高考江苏卷)已知函数f(x)=x3-2x+ex-,其中e是自然对数的底数.若f(a-1)+f(2a2)≤0,则实数a的取值范围是________.
解析:由f(x)=x3-2x+ex-,得f(-x)=-x3+2x+-ex=-f(x),所以f(x)是R上的奇函数,又f′(x)=3x2-2+ex+≥3x2-2+2=3x2≥0,当且仅当x=0时取等号,所以f(x)在其定义域内单调递增,所以不等式f(a-1)+f(2a2)≤0⇔f(a-1)≤-f(2a2)=f(-2a2)⇔a-1≤-2a2,解得-1≤a≤,故实数a的取值范围是.
答案:
9.已知函数f(x)=+-ln x-,其中a∈R,且曲线y=f(x)在点(1,f(1))处的切线垂直于直线y=x.
(1)求a的值;
(2)求函数f(x)的单调区间.
解:(1)对f(x)求导得f′(x)=--(x>0),
由f(x)在点(1,f(1))处的切线垂直于直线y=x,知f′(1)=--a=-2,解得a=.
(2)由(1)知f(x)=+-ln x-,则f′(x)=(x>0).
令f′(x)=0,解得x=-1或x=5.
因为x=-1不在f(x)的定义域(0,+∞)内,故舍去.
当x∈(0,5)时,f′(x)<0,
故f(x)在(0,5)内为减函数;
当x∈(5,+∞)时,f′(x)>0,
故f(x)在(5,+∞)内为增函数.
综上,f(x)的单调增区间为(5,+∞),
单调减区间为(0,5).
10.已知函数f(x)=ln x,g(x)=ax+b.
(1)若f(x)与g(x)在x=1处相切,求g(x)的表达式;
(2)若φ(x)=-f(x)在[1,+∞)上是减函数,求实数m的取值范围.
解:(1)由已知得f′(x)=,
所以f′(1)=1=a,所以a=2.
又因为g(1)=0=a+b,
所以b=-1,
所以g(x)=x-1.
(2)因为φ(x)=-f(x)=-ln x在[1,+∞)上是减函数.
所以φ′(x)=≤0在[1,+∞)上恒成立.
即x2-(2m-2)x+1≥0在[1,+∞)上恒成立,
则2m-2≤x+,x∈[1,+∞),
因为x+∈[2,+∞),
所以2m-2≤2,m≤2.
故实数m的取值范围是(-∞,2].
1.(2017·高考山东卷)若函数exf(x)(e=2.718 28…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质.下列函数中具有M性质的是( )
A.f(x)=2-x B.f(x)=x2
C.f(x)=3-x D.f(x)=cos x
解析:选A.对于选项A,f(x)=2-x=,则exf(x)=ex·=,因为>1,所以exf(x)在R上单调递增,所以f(x)=2-x具有M性质.对于选项B,f(x)=x2,exf(x)=exx2,[exf(x)]′=ex(x2+2x),令ex(x2+2x)>0,得x>0或x<-2;令ex(x2+2x)<0,得-20时,f′(x)>0,f(x)是增函数;当x<0时,f′(x)<0,f(x)是减函数.又f(-3)=f(5)=1,因此不等式f(x)<1的解集是(-3,5).
3.设函数f(x)=ex+x-2,g(x)=ln x+x2-3.若实数a,b满足f(a)=0,g(b)=0,则( )
A.g(a)<00,所以f(a)=0时a∈(0,1).又g(x)=ln x+x2-3在(0,+∞)上单调递增,且g(1)=-2<0,
所以g(a)<0.由g(2)=ln 2+1>0,g(b)=0得b∈(1,2),又f(1)=e-1>0,
所以f(b)>0.综上可知,g(a)<00,函数单调递增,所以由f(x2+2)0),
则h′(x)=--<0,
即h(x)在(0,+∞)上是减函数.
由h(1)=0知,当00,从而f′(x)>0;
当x>1时,h(x)<0,从而f′(x)<0.
综上可知,f(x)的单调递增区间是(0,1),单调递减区间是(1,+∞).
6.设函数f(x)=aln x+,其中a为常数.
(1)若a=0,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性.
解:(1)由题意知a=0时,f(x)=,x∈(0,+∞),
此时f′(x)=,
可得f′(1)=,又f(1)=0,
所以曲线y=f(x)在(1,f(1))处的切线方程为x-2y-1=0.
(2)函数f(x)的定义域为(0,+∞).
f′(x)=+=.
当a≥0时,f′(x)>0,函数f(x)在(0,+∞)上单调递增;
当a<0时,令g(x)=ax2+(2a+2)x+a,
Δ=(2a+2)2-4a2=4(2a+1).
①当a=-时,Δ=0,
f′(x)=≤0,函数f(x)在(0,+∞)上单调递减.
②当a<-时,Δ<0,g(x)<0,
f′(x)<0,函数f(x)在(0,+∞)上单调递减.
③当-0,
设x1,x2(x10,
所以当x∈(0,x1)时,g(x)<0,f′(x)<0,函数f(x)单调递减,
当x∈(x1,x2)时,g(x)>0,f′(x)>0,函数f(x)单调递增,
当x∈(x2,+∞)时,g(x)<0,f′(x)<0,函数f(x)单调递减.
综上可得:当a≥0时,函数f(x)在(0,+∞)上单调递增;
当a≤-时,函数f(x)在(0,+∞)上单调递减;
当-
查看更多