- 2021-05-25 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021高三数学人教B版一轮学案:第八章 第七节 抛物线
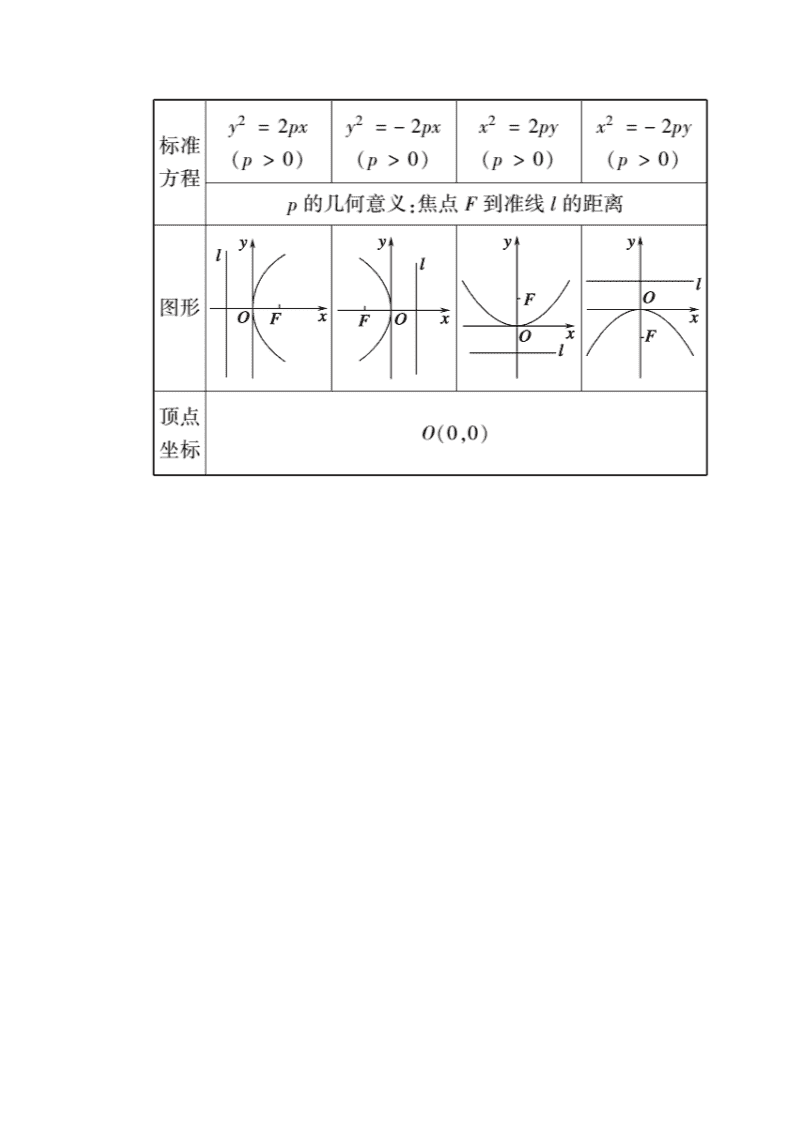
www.ks5u.com 第七节 抛物线 最新考纲 考情分析 1.掌握抛物线的定义、几何图形、标准方程及简单几何性质(范围、对称性、顶点、离心率). 2.理解数形结合的思想. 3.了解抛物线的实际背景及抛物线的简单应用. 1.抛物线的定义、标准方程、几何性质是近几年高考命题的热点. 2.常与圆、椭圆、双曲线、直线、导数等知识交汇命题. 3.题型主要以解答题的形式出现,属于中高档题,有时也会以选择题、填空题的形式出现,属中低档题. 知识点一 抛物线的定义 平面内与一个定点F和一条定直线l(l不经过点F)距离相等的点的轨迹叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线. 数学表达式:|MF|=d(其中d为点M到准线的距离). 当定点在定直线上时,轨迹为过定点F与定直线l垂直的一条直线. 知识点二 抛物线的标准方程及几何性质 抛物线常见的几何性质 1.焦半径、通径:抛物线y2=2px(p>0)上一点P(x0,y0)到焦点F的距离|PF|=x0+,也称为抛物线的焦半径. 过焦点垂直于对称轴的弦称为通径,通径长等于2p,是过焦点最短的弦. 2.直线AB过抛物线y2=2px(p>0)的焦点,交抛物线于A(x1,y1),B(x2,y2)两点,如图可得. ①y1y2=-p2,x1x2=. ②|AB|=x1+x2+p,x1+x2≥2=p,即当x1=x2时,弦长最短为2p. ③+为定值. ④弦长AB=(α为AB的倾斜角). ⑤以AB为直径的圆与准线相切. ⑥焦点F对A,B在准线上射影的张角为90°. 1.思考辨析 判断下列结论正误(在括号内打“√”或“×”) (1)平面内与一个定点F和一条定直线l的距离相等的点的轨迹一定是抛物线.( × ) (2)抛物线y2=4x的焦点到准线的距离是4.( × ) (3)若一抛物线过点P(-2,3),其标准方程可写为y2=2px(p>0).( × ) 2.小题热身 (1)以x=1为准线的抛物线的标准方程为( D ) A.y2=2x B.y2=-2x C.y2=4x D.y2=-4x (2)设抛物线y2=2px(p>0)的焦点在直线2x+3y-8=0上,则该抛物线的准线方程为( D ) A.x=-1 B.x=-2 C.x=-3 D.x=-4 解析:因为抛物线y2=2px的焦点在2x+3y-8=0上,所以p=8,所以抛物线的准线方程为x=-4,故选D. (3)已知点F,直线l:x=-,点B是l上的动点.若过点B垂直于y轴的直线与线段BF的垂直平分线交于点M,则点M的轨迹是( D ) A.双曲线 B.椭圆 C.圆 D.抛物线 解析:由已知得|MF|=|MB|,根据抛物线的定义知,点M的轨迹是以点F为焦点,直线l为准线的抛物线. (4)抛物线8x2+y=0的焦点坐标为. 解析:由8x2+y=0,得x2=-y. ∴2p=,p=,∴焦点为. (5)若抛物线y=4x2上的一点M到焦点的距离为1,则点M的纵坐标是. 解析:M到准线的距离等于M到焦点的距离,又准线方程为y=-,设M(x,y),则y+=1,∴y=. 考点一 抛物线的定义及应用 【例1】 (1)(2020·贵阳市监测考试)抛物线C:y2=2px(p>0)的焦点F到准线l的距离为2,则C的焦点坐标为( ) A.(4,0) B.(2,0) C.(1,0) D.(,0) (2)(2020·广东七校联考)已知抛物线y2=24ax(a>0)上的点M(3,y0)到其焦点的距离是5,则该抛物线的方程为( ) A.y2=8x B.y2=12x C.y2=16x D.y2=20x 【解析】 (1)因为抛物线焦点到准线的距离为2,所以p=2,所以抛物线的方程为y2=4x,抛物线的焦点坐标为(1,0),选C. (2)抛物线y2=24ax(a>0)的准线方程为x=-6a,点M(3,y0)到其焦点的距离是5,根据抛物线的定义可知,点M(3,y0)到准线的距离也为5,即3+6a=5,∴a=,∴y2=8x,故选A. 【答案】 (1)C (2)A 方法技巧 1.已知椭圆+x2=1与抛物线x2=ay有相同的焦点F,O为原点,点P是抛物线准线上一动点,点A在抛物线上,且|AF|=4,则|PA|+|PO |的最小值为( A ) A.2 B.4 C.3 D.4 解析:∵椭圆+x2=1,∴c2=5-1=4,即c=2,则椭圆的焦点为(0,±2),不妨取焦点(0,2),∵抛物线x2=ay,∴抛物线的焦点坐标为,∵椭圆+x2=1与抛物线x2=ay有相同的焦点F,∴=2,即a=8,则抛物线方程为x2=8y,准线方程为y=-2,∵|AF|=4,由抛物线的定义得A到准线的距离为4,y+2=4,即点A的纵坐标y=2,又点A在抛物线上,∴x=±4,不妨取点A坐标为(4,2),A关于准线的对称点的坐标为B(4,-6),则|PA|+|PO|=|PB|+|PO|≥|OB|,即O,P,B三点共线时,有最小值,最小值为|OB|====2,故选A. 2.设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5.若以MF为直径的圆过点A(0,2),则C的方程为( C ) A.y2=4x或y2=8x B.y2=2x或y2=8x C.y2=4x或y2=16x D.y2=2x或y2=16x 解析:由已知得抛物线的焦点F, 设点M(x0,y0), 则=,=. 由已知得,·=0,即y-8y0+16=0, 因而y0=4,M. 由|MF|=5,得=5. 又p>0,解得p=2或p=8. 考点二 抛物线的标准方程及几何性质 【例2】 (1)设F为抛物线C:y2=4x的焦点,M为抛物线C上的一点,O为原点,则使△OFM为等腰三角形的点M的个数为( ) A.1 B.2 C.4 D.6 (2)已知抛物线y2=4x的焦点为F,以F为圆心的圆与抛物线交于M,N两点,与抛物线的准线交于P,Q两点,若四边形MNPQ为矩形,则矩形MNPQ的面积是( ) A.16 B.12 C.4 D.3 【解析】 (1)当|MO|=|MF|时,有2个点M满足题意;当|OM|=|OF|时,有2个点M满足题意.所以点M的个数为4,故选C. (2)根据题意,四边形MNPQ为矩形,可得|PQ|=|MN|,从而得圆心F到准线的距离与到MN的距离相等,所以有M点的横坐标为3,代入抛物线方程,从而求得M(3,2),N(3,-2),所以|MN|=4,|NP|=4,所以矩形MNPQ的面积S=4×4=16. 【答案】 (1)C (2)A 方法技巧 (1)涉及抛物线上的点到焦点的距离或到准线的距离时,常可相互转化;(2)应用抛物线的几何性质解题时,常结合图形思考,通过图形可以直观地看出抛物线的顶点、对称轴、开口方向等几何特征,体现了用数形结合思想解题的直观性. 1.若抛物线y2=4x的焦点是F,准线是l,点M(4,m)是抛物线上一点,则经过点F,M且与l相切的圆有( D ) A.0个 B.1个 C.2个 D.4个 解析:因为点M(4,m)在抛物线y2=4x上,所以可得m=±4.由于圆经过焦点F且与准线l 相切,所以由抛物线的定义知圆心在抛物线上.又圆经过抛物线上的点M,所以圆心在线段FM的垂直平分线上,故圆心是线段FM的垂直平分线与抛物线的交点.结合抛物线的性质知对于点M(4,4)和(4,-4),线段FM的垂直平分线与抛物线都各有2个交点,所以满足条件的圆有4个,故选D. 2.抛物线有如下光学性质:由焦点射出的光线经抛物线反射后平行于抛物线的对称轴;反之,平行于抛物线对称轴的入射光线经抛物线发射后必经过抛物线的焦点.已知抛物线y2=4x的焦点为F,一平行于x轴的光线从点M(3,1)射出,经过抛物线上的点A反射后,再经抛物线上的另一点B射出,则直线AB的斜率为( B ) A. B.- C.± D.- 解析:将y=1,代入y2=4x,可得x=,即A.由抛物线的光学性质可知,直线AB经过焦点F(1,0),所以kAB==-,故选B. 考点三 直线与抛物线的位置关系 命题方向1 焦点弦问题 【例3】 (1)过抛物线y2=8x的焦点F作倾斜角为135°的直线交抛物线于A,B两点,则弦AB的长为( ) A.4 B.8 C.12 D.16 (2)(2020·重庆市调研抽测)已知抛物线C:y2=2px(p>0)的焦点F与双曲线-4y2=1的右焦点相同,过点F分别作两条直线l1,l2,直线l1与抛物线C交于A,B两点,直线l2与抛物线C交于D,E两点,若l1与l2的斜率的平方和为1,则|AB|+|DE|的最小值为( ) A.16 B.20 C.24 D.32 【解析】 (1)抛物线y2=8x的焦点F的坐标为(2,0),直线AB的倾斜角为135°,故直线AB的方程为y=-x+2,代入抛物线方程y2=8x,得x2-12x+4=0.设A(x1,y1),B(x2,y2),则弦AB的长|AB|=x1+x2+4=12+4=16. (2)由双曲线方程知其右焦点坐标为(1,0),所以=1,即p=2,所以抛物线C的方程为y2=4x.由题意可设直线l1的方程为y=k1(x-1)(k1≠0),直线l2的方程为y=k2(x-1)(k2≠0),则k+k=1,于是由消去y,得kx2-(2k+4)x+k=0,所以xA+xB==2+,同理可得,xD+xE=2+.因为F为抛物线的焦点,所以由抛物线的定义可得|AB|+|DE|=(xA++xB+)+(xD++xE+)=xA+xB+xD+xE+2p=2++2++4=8+=8+≥8+=24,当且仅当k=k=时,|AB|+|DE|取得最小值24,故选C. 【答案】 (1)D (2)C 命题方向2 直线与抛物线的位置关系 【例4】 (2020·重庆市七校联考)已知A,B是x轴正半轴上两点(A在B的左侧),且|AB|=a(a>0),过A,B分别作x轴的垂线,与抛物线y2=2px(p>0)在第一象限分别交于D,C两点. (1)若a=p,点A与抛物线y2=2px的焦点重合,求直线CD的斜率; (2)若O为坐标原点,记△OCD的面积为S1,梯形ABCD的面积为S2,求的取值范围. 【解】 (1)由题意知A(,0),则B(+a,0),D(,p),则C(+a,),又a=p,所以kCD==-1. (2)设直线CD的方程为y=kx+b(k≠0),C(x1,y1),D(x2,y2),由,得ky2-2py+2pb=0, 所以Δ=4p2-8pkb>0,得kb<, 又y1+y2=,y1y2=,由y1+y2=>0,y1y2=>0,可知k>0,b>0, 因为|CD|=|x1-x2|=a, 点O到直线CD的距离d=, 所以S1=·a·=ab. 又S2=(y1+y2)·|x1-x2|=··a=, 所以=,因为0查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档