数学华东师大版八年级上册教案14-1 第2课时 验证勾股定理

数学华东师大版八年级上册教案14-1 第2课时 验证勾股定理

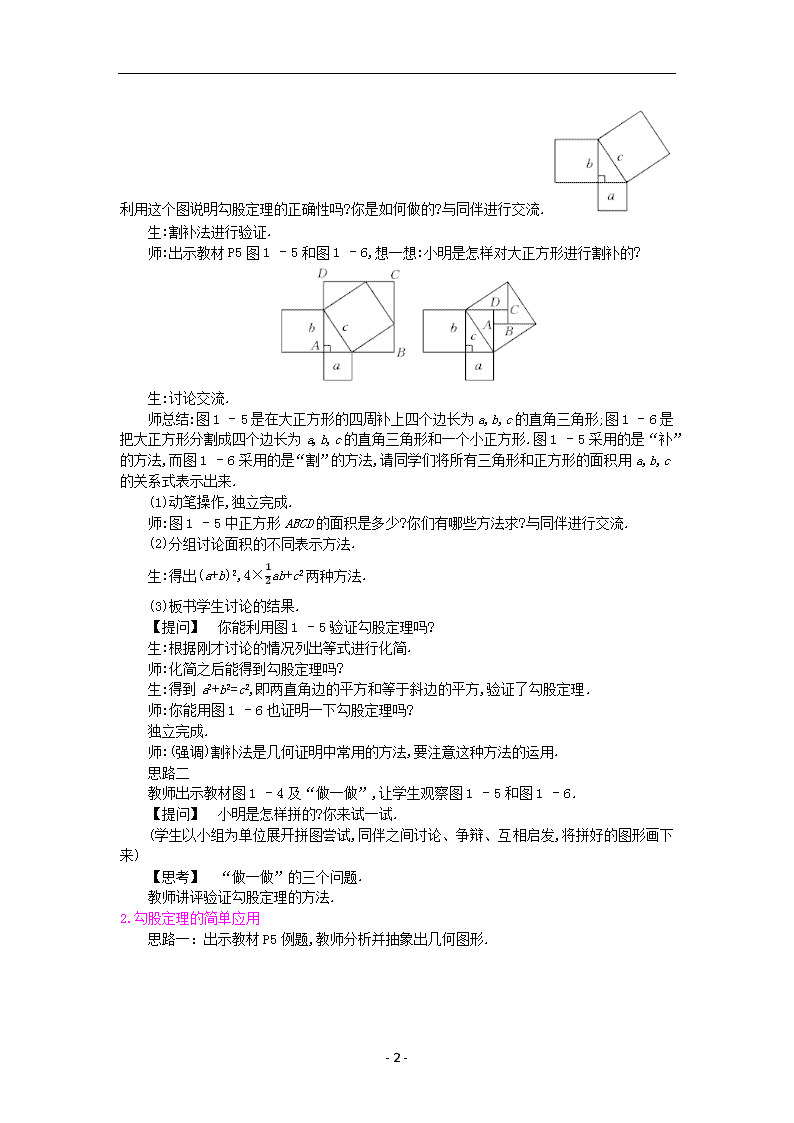
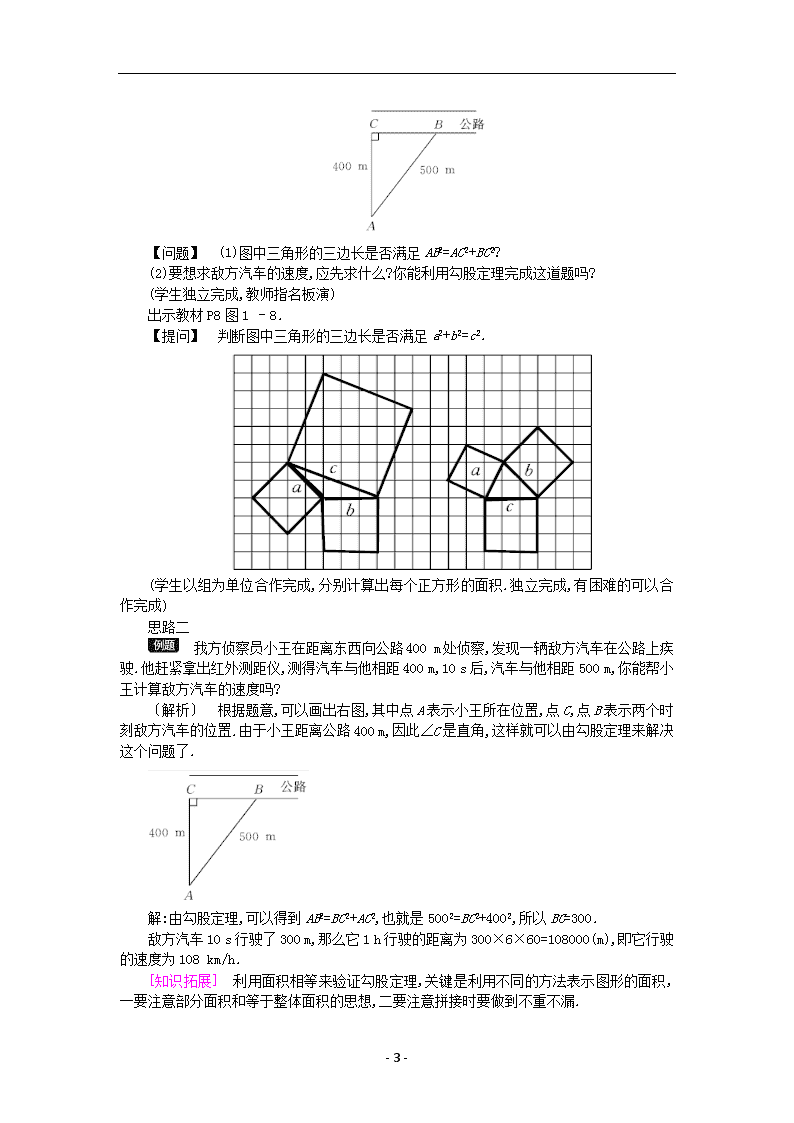
- 1 - 1.1 探索勾股定理 第 2 课时 验证勾股定理 教学目标 【知识与能力】 1.掌握勾股定理,理解和利用拼图验证勾股定理的方法. 2.能运用勾股定理解决一些简单的实际问题. 【过程与方法】 通过拼图法验证勾股定理,使学生经历观察、猜想、验证的过程,进一步体会数形结合的思想. 【情感态度价值观】 培养学生大胆探索,不怕失败的精神. 教学重难点 【教学重点】 经历勾股定理的验证过程,能利用勾股定理解决实际问题. 【教学难点】 用拼图法验证勾股定理. 课前准备 【教师准备】教材图 1 - 4,1 - 5,1 - 6,1 - 7 的图片. 【学生准备】4 个全等的直角三角形纸片. 教学过程 第一环节：引入新课 导入一: 【提问】 直角三角形的三边有怎样的关系?在研究直角三角形三边关系时,我们是通过 测量、数格子的方法发现了勾股定理,那么,我们怎样用科学的方法去证明勾股定理的正确性 呢?请跟我一起去探索吧! 导入二: 上节课我们用什么方法探索发现了勾股定理? 学生思考(测量、数格子). 第二环节：新知构建 [过渡语] 一样的科学结论,可能会有很多的证明方式,人们对勾股定理的验证,就给出 了多种的证明方式,我们也一起来尝试下吧. 1.勾股定理的验证 思路一 【师生活动】 师:投影教材 P4 图 1 - 4,分别以直角三角形的三条边的长度为边长向外作正方形,你能 利 用 这 个 图 说 明 勾 股 定 理 的 正 确 性 吗 ? 你 是 如 何 做 的 ? 与 同 伴 进 行 交 流 . - 2 - 生:割补法进行验证. 师:出示教材 P5 图 1 - 5 和图 1 - 6,想一想:小明是怎样对大正方形进行割补的? 生:讨论交流. 师总结:图 1 - 5 是在大正方形的四周补上四个边长为 a,b,c 的直角三角形;图 1 - 6 是把大正方形分割成四个边长为a,b,c的直角三角形和一个小正方形.图1 - 5采用的是“补” 的方法,而图 1 - 6 采用的是“割”的方法,请同学们将所有三角形和正方形的面积用 a,b,c 的关系式表示出来. (1)动笔操作,独立完成. 师:图 1 - 5 中正方形 ABCD 的面积是多少?你们有哪些方法求?与同伴进行交流. (2)分组讨论面积的不同表示方法. 生:得出(a+b)2,4× 1 2 ab+c2 两种方法. (3)板书学生讨论的结果. 【提问】 你能利用图 1 - 5 验证勾股定理吗? 生:根据刚才讨论的情况列出等式进行化简. 师:化简之后能得到勾股定理吗? 生:得到 a2+b2=c2,即两直角边的平方和等于斜边的平方,验证了勾股定理. 师:你能用图 1 - 6 也证明一下勾股定理吗? 独立完成. 师:(强调)割补法是几何证明中常用的方法,要注意这种方法的运用. 思路二 教师出示教材图 1 - 4 及“做一做”,让学生观察图 1 - 5 和图 1 - 6. 【提问】 小明是怎样拼的?你来试一试. (学生以小组为单位展开拼图尝试,同伴之间讨论、争辩、互相启发,将拼好的图形画下 来) 【思考】 “做一做”的三个问题. 教师讲评验证勾股定理的方法. 2.勾股定理的简单应用 思路一：出示教材 P5 例题,教师分析并抽象出几何图形. - 3 - 【问题】 (1)图中三角形的三边长是否满足 AB2=AC2+BC2? (2)要想求敌方汽车的速度,应先求什么?你能利用勾股定理完成这道题吗? (学生独立完成,教师指名板演) 出示教材 P8 图 1 - 8. 【提问】 判断图中三角形的三边长是否满足 a2+b2=c2. (学生以组为单位合作完成,分别计算出每个正方形的面积.独立完成,有困难的可以合 作完成) 思路二 我方侦察员小王在距离东西向公路 400 m 处侦察,发现一辆敌方汽车在公路上疾 驶.他赶紧拿出红外测距仪,测得汽车与他相距 400 m,10 s 后,汽车与他相距 500 m,你能帮 小王计算敌方汽车的速度吗? 〔解析〕 根据题意,可以画出右图,其中点 A 表示小王所在位置,点 C,点 B 表示两个时 刻敌方汽车的位置.由于小王距离公路 400 m,因此∠C 是直角,这样就可以由勾股定理来解决 这个问题了. 解:由勾股定理,可以得到 AB2=BC2+AC2,也就是 5002=BC2+4002,所以 BC=300. 敌方汽车 10 s 行驶了 300 m,那么它 1 h 行驶的距离为 300×6×60=108000(m),即它行 驶的速度为 108 km/h. [知识拓展] 利用面积相等来验证勾股定理,关键是利用不同的方法表示图形的面积, 一要注意部分面积和等于整体面积的思想,二要注意拼接时要做到不重不漏. - 4 - 曾任美国总统的伽菲尔德在《新英格兰教育日志》上发表了他提出的一个勾股定理证明, 如图所示,这就是他拼出的图形.它的面积有两种表示方法,既可以表示为 1 2 (a+b)(a+b),又可 以表示为 1 2 (2ab+c2),所以可得 1 2 (a+b)(a+b)= 1 2 (2ab+c2),化简可得 a2+b2=c2. 第三环节：课堂小结 1.勾股定理的验证方法 测量法 数格子法 面积法 2.在实际问题中,首先要找到直角三角形,然后再应用勾股定理解题. 第四环节：检测反馈 1.下列选项中,不能用来证明勾股定理的是 ( ) 解析:A,B,C 都可以利用图形面积得出 a,b,c 的关系,即可证明勾股定理,故 A,B,C 选项 不符合题意;D,不能利用图形面积证明勾股定理,故此选项正确.故选 D. 2.用四个边长均为 a,b,c 的直角三角板,拼成如图所示的图形,则下列结论中正确的是 ( ) A.c2=a2+b2 B.c2=a2+2ab+b2 C.c2=a2-2ab+b2 D.c2=(a+b)2 - 5 - 解析:由题意得到四个完全一样的直角三角板围成的四边形为正方形,其边长为 c,里面 的小四边形也为正方形,边长为 b-a,则有 c2= 1 2 ab×4+(b-a)2,整理得 c2=a2+b2.故选 A. 3.如图所示,大正方形的面积是 ,另一种方法计算大正方形的面积是 , 两种结果相等,推得勾股定理是 . 解析:如图所示,大正方形的面积是(a+b)2,另一种计算方法是 4× 1 2 ab+c2,即(a+b)2=4× 1 2 ab+c2,化简得 a2+b2=c2. 答案:(a+b)2 4× 1 2 ab+c2 a2+b2=c2 4.操作:剪若干个大小形状完全相同的直角三角形,三边长分别记为 a,b,c(如图(1)所 示),分别用 4 张这样的直角三角形纸片拼成如图(2)(3)所示的形状,图(2)中的两个小正方 形的面积 S2,S3 与图(3)中小正方形的面积 S1 有什么关系?你能得到 a,b,c 之间有什么关系? 解析:根据已知图形的形状得出面积关系,进一步证明勾股定理即可求解. 解:分别用 4 张直角三角形纸片,拼成如图(2)(3)所示的形状,观察图(2)(3)可发现,图 (2)中的两个小正方形的面积之和等于图(3)中的小正方形的面积,即 S2+S3=S1,这个结论用关 系式可表示为 a2+b2=c2. 第五环节：布置作业 1.教材作业 【必做题】 教材第 6 页随堂练习. 【选做题】 教材第 7 页习题 1.2 第 3 题. 2.课后作业 【基础巩固】 1.我国古代数学家赵爽的《勾股圆方图》是由四个全等的直角三角形与中间的一个小正方形 拼成的一个大正方形(如图所示).如果大正方形的面积是 13,小正方形的面积是 1,直角三角 . D,E,F,G,H,I 都在矩形 KLMJ 的边上,则矩形 KLMJ 的面积为 关系验证 勾股定理.图(2) 是由图(1)放入矩形 内得到的, ∠BAC=90°,AB=6,AC=8,点 弦五”的记载.如图(1)所示的是由边长相等的小正方形和直角三角形构成的,可以用其面积 4.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则 【能力提升】 (3)如果 a2+b2=100,a+b=14,求此直角三角形的面积. 出验证过程) (2)请用四个这样的直角三角形再拼出另一个几何图形,也能验证(1)中所写的等式.(不用写 关于 a,b,c 的等式.(要有过程) 个 (1)它可以看做是由四个边长分别为 a,b,c 的直角三角形拼成的,请从面积关系出发,写出一 北京召开的第 24 届国际数学家大会会标的图案如图所示..3‸ت㈳ 四边形 = ت Δ ‸ + Δ ‸㈳ + Δ D. ت‸ 四边形 ‸㈳ = 四边形 ‸C. Δ = ت Δ ‸㈳ + Δ B. ت Δ ‸㈳ = Δ A. AE,EB 在一条直线上.证明中用到的面积相等的关系是 ( ) 2.历史上对勾股定理的一种证法采用了如图所示的图形,其中两个全等的直角三角形边 A.1 B.2 C.12 D.13 形的两直角边长分别为 a,b,那么(a-b)2 的值是 ( ) - 6 - - 7 - 5.在北京召开的国际数学家大会的会标如图所示,它是由四个相同的直角三角形与中间的小 正方形拼成的一个大正方形,若大正方形的面积是 13,小正方形的面积是 1,直角三角形的较 长直角边为 a,较短直角边为 b,则 a4+b4 的值为( ) A.35 B.43 C.89 D.97 6.据传当年毕达哥拉斯借助如图所示的两个图验证了勾股定理,你能说说其中的道理吗? 7.如图所示,在平面内,把矩形 ABCD 绕点 B 按顺时针方向旋转 90°得到矩形 A'BC'D'.设 AB=a,BC=b,BD=c.请利用该图验证勾股定理. 【拓展探究】 8.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如 图(1)所示).图(2)是由弦图变化得到的,它是用八个全等的直角三角形拼接而成的.记图中 正方形 ABCD,正方形 EFGH,正方形 MNKT 的面积分别为 S1,S2,S3.若 S1+S2+S3=16,则 S2 的值是 . 9.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感, 他惊喜地发现,当两个全等的直角三角形如图(1)或图(2)摆放时,都可以用“面积法”来证明, 下 面 是 小 聪 利 用 图 (1) 证 明 勾 股 定 理 的 过 程 . .× 48=24 2 1 ab= 2 1 (2) 如 图 所 示 . (3) ∵ 2ab=(a+b)2-(a2+b2)=196-100=96, ∴ ab=48, ∴ S= ab+(a-b)2=a2+b2. 2 1 3.解:(1)大正方形的面积=4 个三角形的面积+小正方形的面积,即 c2=4× 故选 D.). ‸ت㈳ 四边形 = ت Δ ‸ + Δ ‸㈳ + Δ c2+2ab=a2+2ab+b2,整理得 a2+b2=c2,∴证明中用到的面积相等的关系是 (a+b)2, ∴ 2 1 ab= 2 1 c2+ 2 1 ab+ 2 1 可 知 , ‸ت㈳ 四边形 = ت Δ ‸ + Δ ‸㈳ + Δ 2.D( 解 析 : 由 2ab=12,则(a-b)2=a2-2ab+b2=13-12=1.故选 A.) ab×4=13-1=12,即 2 1 1.A(解析:根据勾股定理可得 a2+b2=13,四个直角三角形的面积和是 【答案与解析】 a2+b2=c2.∴ , ∴ , = ‸ت㈳ 五边形 又∵ , = ‸ت㈳ 五边形 ∵ 证明:连接 , 验证 a2+b2=c2. 将两个全等的直角三角形按图(2)所示摆放,其中∠DAB=90°,连接 BE. 请参照上述证法,利用图(2)完成下面的验证过程. ∴a2+b2=c2. a(b-a), 2 1 c2+ 2 1 ab= 2 1 b2+ 2 1 ∴ a(b-a), 2 1 c2+ 2 1 = ت‸ Δ + ت‸㈳ Δ = ت‸㈳ 四边形 又∵ ab, 2 1 b2+ 2 1 = ت㈳ Δ ㈳‸ + Δ = ت‸㈳ 四边形 ∵ 证明:连接 DB,过点 D 作 BC 边上的高 DF,则 DF=EC=b-a. 将两个全等的直角三角形按图(1)所示摆放,连接 DC,其中∠DAB=90°,求证 a2+b2=c2. - 8 - ∴ ,(a(b-a 2 1 c2+ 2 1 ab+ 2 1 ab, 又 ∵ S 五 边 形 ACBED=S Δ ACB+S Δ ABD+S Δ BDE= 2 1 b2+ 2 1 ab+ 2 1 ADE= S Δ+ ت㈳ Δ 9. 证 明 : 连 接 BD, 过 点 B 作 DE 边 上 的 高 BF, 则 BF=b-a, ∵ S 五 边 形 ACBED=S Δ ACB+ .) 3 16 .故答案为 3 16 ,∴S2= 3 16 S1+S2+S3=GF2+2CG·DG+GF2+NG2+NF2-2NG·NF=3GF2=16,∴GF2= ∴ S1=(CG+DG)2=CG2+DG2+2CG · DG=GF2+2CG · DG,S2=GF2,S3=(NG-NF)2=NG2+NF2-2NG · NF, ∴ (解析:∵八个直角三角形全等,四边形ABCD,EFGH,MNKT是正方形,∴CG=NG,CF=DG=NF=GK, 3 16 8. 此 a2+b2=c2. c2+ab,因 2 1 (a2+b2)+ab= 2 1 c2+ab,∴ 2 1 ab= 2 1 c2+2× 2 1 (a2+b2)+ab,又 S=SRtΔDBD'+2SRtΔABD= 2 1 (a+b)(a+b)= 2 1 S= DAB 和 Rt Δ BC'D' 的 形 状 和 大 小 完 全 一 样 , 设 梯 形 DAC'D' 的 面 积 为 S, 则 7.解:连接 D'D,依题意,图中的四边形 DAC'D'为直角梯形,ΔDBD'为等腰直角三角形,RtΔ 和. a,b 的直角三角形的面积和,∴a2+b2=c2,即在直角三角形中斜边的平方等于两直角边的平方 形的面积的和是 a2+b2,∵它们的面积都等于边长为 a+b 的正方形的面积-4 个直角边分别为 6.解:根据题意,第一个图形中间空白小正方形的面积是 c2;第二个图形中空白的两个小正方 =13-1=12,ab=6,则 a4+b4=(a2+b2)2-2a2b2=(a2+b2)2-2(ab)2=132-2×62=169-72=97.故选 D.) 5.D( 解 析 : 依 题 意 有 :a2+b2= 大 正 方 形 的 面 积 =13,2ab= 四 个 直 角 三 角 形 的 面 积 和 形 KLMJ 的面积=22×20=440.故答案为 440.) PB=AC=8,CQ=AB=6,∵图(2)是由图(1)放入矩形内得到的,∴IP=8+6+8=22,DQ=6+8+6=20,∴矩 解析:如图所示,延长 AB 交 KL 于 P,延长 AC 交 LM 于 Q,则ΔABC≌ΔPFB≌ΔQCG,∴)4.440 - 9 - - 10 - 1 2 ab+ 1 2 b2+ 1 2 ab= 1 2 ab+ 1 2 c2+ 1 2 a(b-a),∴a2+b2=c2. 板书设计 1.1.2 1.勾股定理的验证. 2.勾股定理的简单应用. 教学反思 成功之处 在课堂教学中,始终注意了调动学生的积极性.兴趣是最好的老师,所以无论是引入、拼 图,还是历史回顾,都注意去调动学生,让学生满怀激情地投入到活动中.勾股定理作为“千古 第一定理”,其魅力在于其历史价值和应用价值,因此充分挖掘了其内涵.特别是让学生事先 进行调查,再在课堂上进行展示,这极大地调动了学生的积极性,既加深了对勾股定理文化的 理解,又培养了学生收集、整理资料的能力. 不足之处 在教学过程中,过于让学生发散思维,而导致课堂秩序略有松散. 再教设计 勾股定理的验证既是本节课的重点,也是本节课的难点,为了突破这一难点,可以设计拼 图活动,先让学生从形上感知,再层层设问,从面积(数)入手,师生共同探究,最后由学生独立 探究,这样学生较容易突破本节课的难点. 备课资源 古诗中的数学题 请你先欣赏下面一首诗: 平平湖水清可鉴,面上半尺生红莲; 出泥不染亭亭立,忽被强风吹一边; 渔人观看忙向前,花离原位两尺远; 能算诸君请解题,湖水如何知深浅? 你能用所学的数学知识解决上述诗中的问题吗? 〔解析〕 要解决诗中提出的问题,关键是将实际问题转化为数学问题,画出符合题意的 图形,如图所示.在 RtΔBCD 中,由勾股定理建立方程求线段的长. 解:如图所示,AD 表示莲花的高度,CD 是水的深度,CB 是莲花吹倒后离原位的距离. - 11 - 设 CD=x 尺,则 AD=BD= + 1 2 尺. 在 RtΔBCD 中,∠BCD=90°,由勾股定理得 BD2=CD2+BC2,即 + 1 2 2 =22+x2. 解得 x=3.75. 所以所求的湖水深度为 3.75 尺. [方法总结] 建立数学模型是解决实际问题的常用方法.本例是利用莲花无风时与水面 垂直构造直角三角形这一几何模型.在直角三角形中常用勾股定理建立方程求线段的长.