- 2021-05-25 发布 |
- 37.5 KB |
- 7页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考理科二面角和二面角的求法
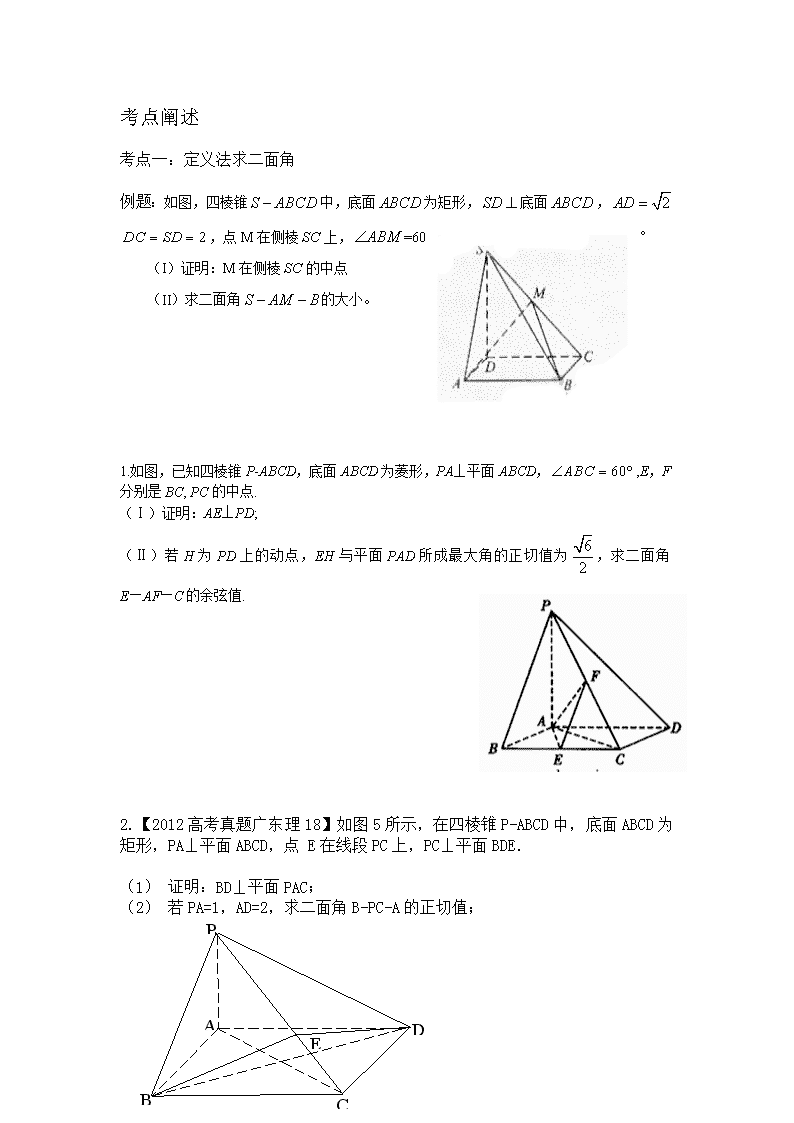
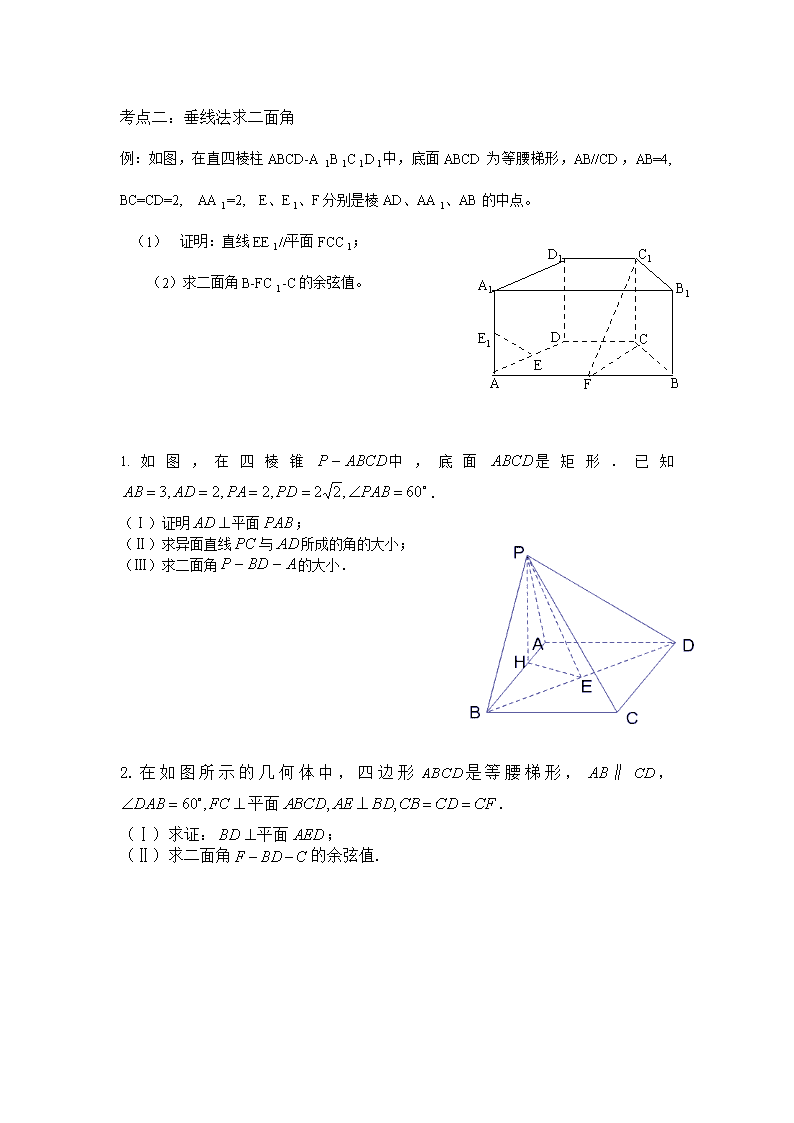
二面角和二面角的求法 知识清单 1.二面角的定义: 从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二 面角的棱,这两个半平面叫做二面角的面。 2.二面角的平面角:以二面角的棱上任意一点为顶点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫二面角的平面角。 3.直二面角:平面角是直角的二面角叫直二面角。两相交平面如果所组成的二面角是直二面角,那么这两个平面垂直; 反过来,如果两个平面垂直,那么所成的二面角为直二面角 4.求二面角的方法 (1)定义法:在棱上选择有关点,过这个点分别在两个面内作垂直于棱的射线得到平面角 (2)垂线法 三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.通常当点P在一个半平面上则通常用三垂线定理法求二面角的大小。 (3)射影面积法 凡二面角的图形中含有可求原图形面积和该图形在另一个半平面上的射影图形面积的都可利用射影面积公式(cos)求出二面角的大小。 (4) 向量法 考点阐述 考点一:定义法求二面角 例题:如图,四棱锥中,底面为矩形,底面, ,点M在侧棱上,=60° (I)证明:M在侧棱的中点 (II)求二面角的大小。 1.如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,,E,F分别是BC, PC的中点. (Ⅰ)证明:AE⊥PD; (Ⅱ)若H为PD上的动点,EH与平面PAD所成最大角的正切值为,求二面角E—AF—C的余弦值. 2.【2012高考真题广东理18】如图5所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点 E在线段PC上,PC⊥平面BDE. (1) 证明:BD⊥平面PAC; P A B C D E (2) 若PA=1,AD=2,求二面角B-PC-A的正切值; 考点二:垂线法求二面角 E A B C F E1 A1 B1 C1 D1 D 例:如图,在直四棱柱ABCD-ABCD中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA=2, E、E、F分别是棱AD、AA、AB的中点。 (1) 证明:直线EE//平面FCC; (2)求二面角B-FC-C的余弦值。 1.如图,在四棱锥中,底面是矩形.已知. (Ⅰ)证明平面; (Ⅱ)求异面直线与所成的角的大小; (Ⅲ)求二面角的大小. 2.在如图所示的几何体中,四边形是等腰梯形,∥,平面. (Ⅰ)求证:平面; (Ⅱ)求二面角的余弦值. 3.如图,在三棱锥中,,,,平面平面。 (Ⅰ)求直线与平面所成角的大小; (Ⅱ)求二面角的大小。 考点三:射影面积法求二面角 例题:如图,在三棱锥中,,, A C B P ,. (Ⅰ)求证:; (Ⅱ)求二面角的余弦值的大小; A1 D1 B1 C1 E D B C A 图5 1.如图5,E为正方体ABCD-A1B1C1D1的棱CC1的中点,求平面AB1E和底面A1B1C1D1所成锐角的余弦值. 2.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1. (Ⅰ)证明PC⊥AD; (Ⅱ)求二面角A-PC-D的余弦值; 3.如图,已知正三棱柱-的底面边长为2,侧棱长为,点E在侧棱上,点F在侧棱上,且,. (I) 求证:; (II) 求二面角的大小。 考点四:向量法求二面角 例题:如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5. (Ⅰ)求证:AA1⊥平面ABC; (Ⅱ)求二面角A1-BC1-B1的余弦值; 1.如图,直三棱柱中,,是棱的中点, (1)证明: (2)求二面角的大小. B1 C1 A1 D C A B 2.如图,在四棱锥P—ABCD中,底面是边长为的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=,M,N分别为PB,PD的中点. (Ⅰ)证明:MN∥平面ABCD; (Ⅱ) 过点A作AQ⊥PC,垂足为点Q,求二面角A—MN—Q的平面角的余弦值. A D B C M P Q N 3.如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=P D. (I)证明:平面PQC⊥平面DCQ; (II)求二面角Q—BP—C的余弦值.查看更多