- 2021-05-25 发布 |
- 37.5 KB |
- 21页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级数学上册第13章全等三角形13-2三角形全等的判定第5课时斜边直角边作业课件新版华东师大版
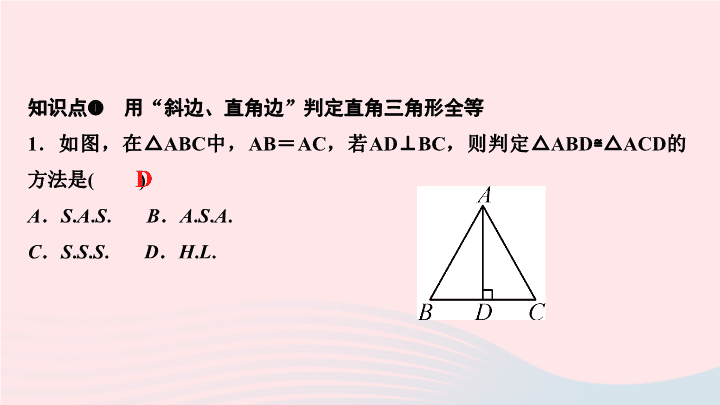
第13章 全等三角形 13.2 三角形全等的判定 第5课时 斜边直角边 知识点 ❶ 用 “ 斜边、直角边 ” 判定直角三角形全等 1 .如图,在△ ABC 中, AB = AC ,若 AD⊥BC ,则判定△ ABD≌△ACD 的方法是 ( ) A . S . A . S . B . A . S . A . C . S . S . S . D . H . L . D 2 .使两个直角三角形全等的条件是 ( ) A .一个锐角对应相等 B .两个锐角对应相等 C .一条边对应相等 D .两条边对应相等 D 3 .如图,已知 AB⊥AC , CD⊥BD ,若用“ H . L .” 证明△ ABC≌△DCB ,则还应添加条件 _____________________ ;若用“ A . A . S .” 证明△ ABC≌△DCB ,则还应添加条件 ________________________________ . AB = DC 或 AC = DB ∠ ABC =∠ DCB 或∠ ACB =∠ DBC 4 . ( 孝感中考 ) 如图,已知 AB = CD , AE⊥BD , CF⊥BD ,垂足分别为 E , F , BF = DE ,求证: AB∥CD. 知识点 ❷ 直角三角形全等的综合判定 5 .如图,已知 AB = AD ,那么添加下列一个条件后,仍无法判定△ ABC≌△ADC 的是 ( ) A . CB = CD B .∠ BAC =∠ DAC C .∠ BCA =∠ DCA D .∠ B =∠ D = 90° C 6 .如图, AD , A′D′ 分别是锐角△ ABC 和锐角△ A′B′C′ 的 BC , B′C′ 边上的高,且 AB = A′B′ , AD = A′D′ ,若使△ ABC≌△A′B′C′ ,请你补充条件 _______________( 答案不唯一 ) . ( 填一个你认为适当的条件 ) AC = A′C′ 7 .下列命题: ① 两直角边对应相等的两个直角三角形全等; ② 两锐角对应相等的两个直角三角形全等; ③ 斜 边和一直角边对应相等的两个直角三角形全等; ④ 一锐角和一直角边对应相等的两个直角三角形全等; ⑤ 一锐角和斜边对应相等的两个直角三角形全等. 其中正确的命题有 ____________ . ( 填序号 ) ①③④⑤ 8 .如图, CD⊥AB , BE⊥AC ,垂足分别为 D , E , BE 与 CD 相交于点 O ,且 AD = AE. 有下列结论: ①∠ B = ∠ C ; ②△ ADO ≌△ AEO ; ③△ BOD ≌△ COE ; ④ 图中有四组三角形全等. 其中正确的结论有 ( ) A .1 个 B . 2 个 C . 3 个 D . 4 个 D 9 .如图, BE⊥AC , CF⊥AB ,垂足分别是 E , F , BE , CF 相交于点 O ,若 BE = CF ,则图中共有 ____ 对全等三角形. 3 10 .如图,在 Rt △ABC 中,∠ C = 90° , AC = 7 , BC = 3 ,一条线段 PQ = AB , P , Q 两点分别在 AC 和与 AC 垂直的射线 AX 上移动, 当 AP = __________ 时,才能使△ ABC 与△ QPA 全等. 3 或 7 11 . ( 郸城月考 ) 如图,在△ ABC 中,∠ BAC = 90° , AB = AC , D 在 AC 上, E 在 BA 的延长线上, BD = CE , BD 的延长线交 CE 于点 F ,求证: BF⊥CE. 证明:∵ BD = CE , AB = AC ,∴ Rt △BAD≌ Rt △CAE( H . L .) ,∴∠ ADB =∠ E.∵∠BAC = 90° ,∴∠ EBF +∠ ADB = 90° ,∴∠ EBF +∠ E = 90° ,∴∠ BFE = 90° ,即 BF⊥CE 12 . ( 习题 2 变式 ) 如图,已知 AE⊥BC , DF⊥BC , E , F 是垂足, AE = DF , AB = DC ,求证: AC = DB. 证明:先证△ ABE≌△DCF( H . L .) ,再证△ ABC≌△DCB ,即可得出结论 13 . ( 习题 1 变式 ) 如图,在△ ABC 中, D 是 BC 的中点, DE⊥AB , DF⊥AC ,垂足分别为点 E , F ,且 DE = DF. 求证: AB = AC. 证明:连结 AD ,先证 Rt △BDE≌ Rt △CDF ,得 BE = CF ,再证 Rt △ADE≌ Rt △ADF ,得 AE = AF ,∴ BE + AE = CF + AF ,即 AB = AC 14 . ( 例题 7 变式 ) 如图, AB = AC ,点 D , E 分别在 AC , AB 上, AG⊥BD 于点 G , AF⊥CE 于点 F ,且 AG = AF. 求证: BD = CE. 证明:先证 Rt △ABG≌ Rt △ACF ,得∠ B =∠ C , 再证△ ABD≌△ACE ,即可得出结论 15 .如图①,点 A , E , F , C 在同一条直线上, AE = CF ,过点 E , F 分别作 DE⊥AC , BF⊥AC ,连结 AB , CD , BD , BD 交 AC 于点 G ,且 AB = CD. (1) 试证明 BD 与 EF 互相平分; (2) 若将△ DEC 的边 EC 沿 AC 方向移动变为图②时,其余条件不变, (1) 中结论是否仍成立?请说明理由.查看更多