- 2021-05-24 发布 |
- 37.5 KB |
- 3页

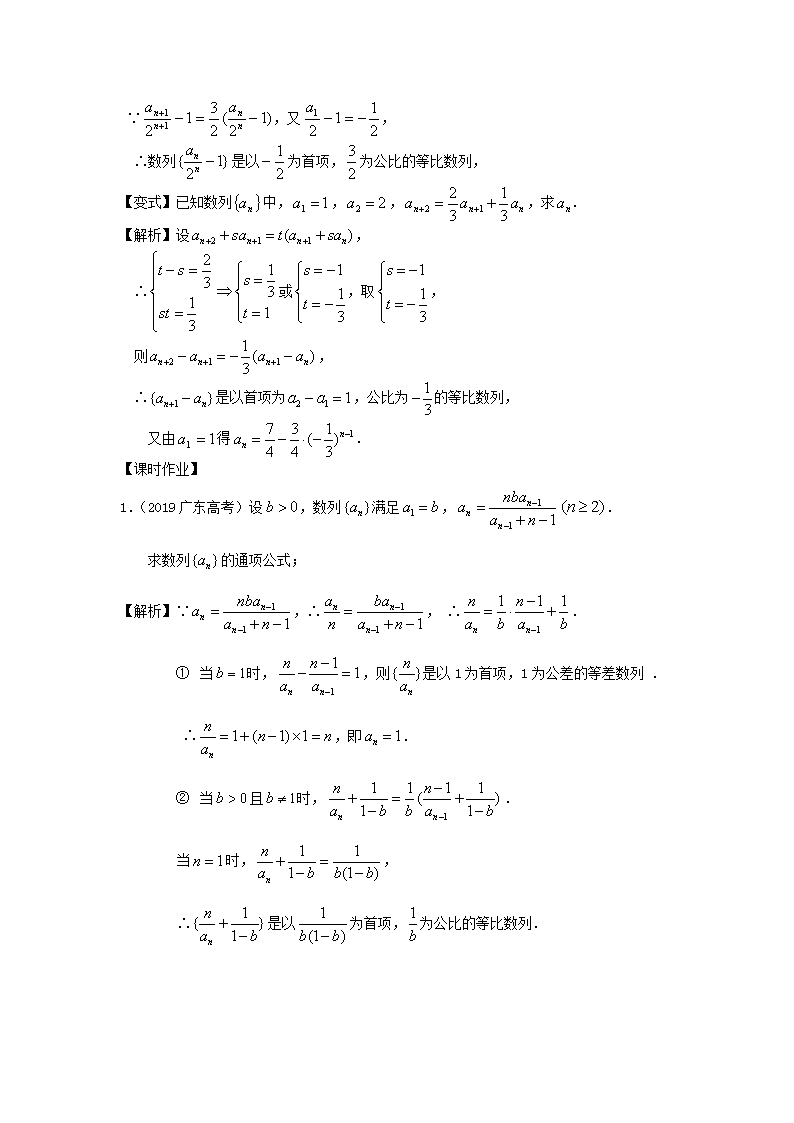
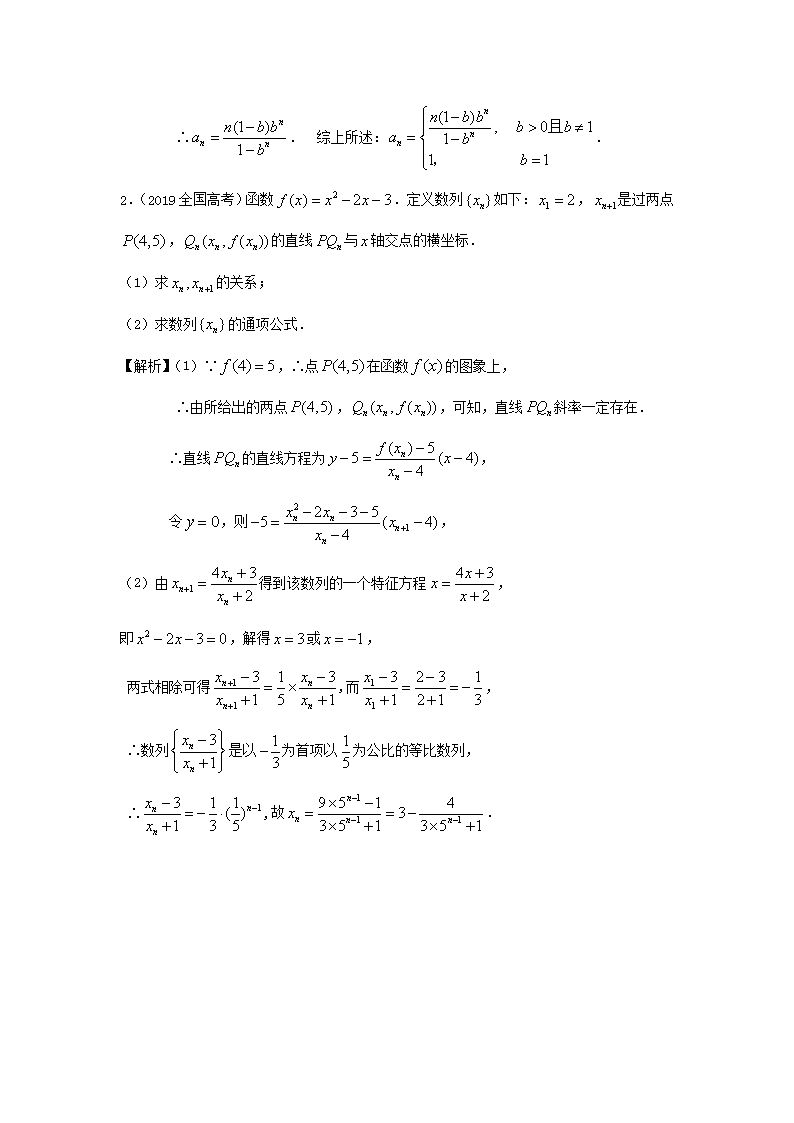
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
三维设计广东文人教版2014高考数学第一轮复习考案 递推数列求通项1 文
第44课 递推数列求通项(1) 【补充题型】 1.递推公式形如(其中p、q、r、h均为常数,且) 方法:作特征方程,解出. 【例1】已知数列满足:对于都有. (1)若,求; (2)若,求. 【解析】作特征方程,∴,∴. (1)∵,∴. (2)∵,∴, ∴数列是以为首项,以为公差的等差数列, ∴数列从第5项开始都不存在,∴当,时,. 【变式】已知数列满足性质:对于,且,求的通项公式. 【解析】作特征方程,∴,解得或. ∴数列是以为首项,以为公比的等比数列, 2.递推公式形如 方法:①设, ②解出,的值,其中,满足, ③再用换元法转化为等比数列求解. 【例2】(2019汕头质检)已知数列中,,,求. 【解析】设,∴. ∴或,取,则, ∴是以首项为,公比为的等比数列, ∵,又, ∴数列是以为首项,为公比的等比数列, 【变式】已知数列中,,,,求. 【解析】设, ∴或,取, 则, ∴是以首项为,公比为的等比数列, 又由得. 【课时作业】 1.(2019广东高考)设,数列满足,. 求数列的通项公式; 【解析】∵,∴, ∴. ① 当时,,则是以1为首项,1为公差的等差数列 . ∴,即. ② 当且时,. 当时,, ∴是以为首项,为公比的等比数列. ∴. 综上所述:. 2.(2019全国高考)函数.定义数列如下:,是过两点,的直线与轴交点的横坐标. (1)求的关系; (2)求数列的通项公式. 【解析】(1)∵,∴点在函数的图象上, ∴由所给出的两点,,可知,直线斜率一定存在. ∴直线的直线方程为, 令,则, (2)由得到该数列的一个特征方程, 即,解得或, 两式相除可得,而, ∴数列是以为首项以为公比的等比数列, ∴,故.查看更多