- 2021-05-24 发布 |
- 37.5 KB |
- 22页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级上册青岛版数学课件2-5解直角三角形的应用
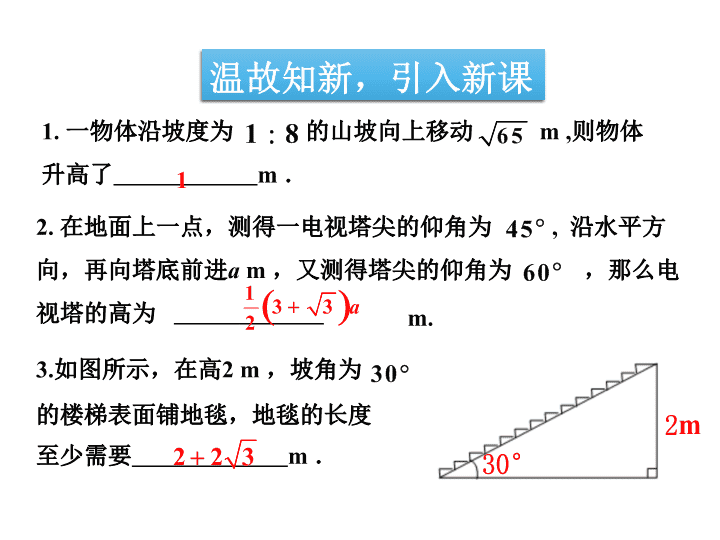
2.5解直角三角形的应用 1. 一物体沿坡度为 的山坡向上移动 m ,则物体 升高了 m . 1 8 65 2. 在地面上一点,测得一电视塔尖的仰角为 , 沿水平方 向,再向塔底前进a m ,又测得塔尖的仰角为 ,那么电 视塔的高为 45 60 3.如图所示,在高2 m ,坡角为 的楼梯表面铺地毯,地毯的长度 至少需要 m . 30 1 3 32 a 2 2 3 1 m. 温故知新,引入新课 w如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮四 由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里 后到达该岛的南偏西25°的C处.之后,货轮继续向东航行. w请与同伴交流你是怎么想的? 怎么去做? w你认为货轮继续向东航行途中会有触礁的危险吗? A 导学知识,合作探究 1.思路点拔 (2)请同学们根据题意在练习本上画出示意图,然后说明你 是怎样画出来的. A B C D 北 东 (1)我们注意到题中有很多方位,在平面图形中,方位是如何 规定的? 应该是“上北下南,左西右东”. 首先我们可将小岛A确定, 货轮B在小岛A的南偏西 55°的B处,C在B的正东 方,且在A南偏东25°处. 示意图如右. (3)货轮要向正东方向继续行驶,有没有触礁的危险,由谁 来决定? 根据题意,小岛四周10海里内有暗礁,那么货轮继续向东航行的 方向如果到A的最短距离大于10海里,则无触礁的危险,如果小 于10海里则有触礁的危险.A到BC所在直线的最短距离为过A作 AD⊥BC,D为垂足,即AD的长度.我们需根据题意,计算出AD 的长度,然后与10海里比较. A B C D 北 东 (4)下面我们就来看AD如何求.根据题意,有哪些已知条件呢? 已知BC=20海里,∠BAD=55°,∠CAD=25°. (5)在示意图中,有两个直角三 角形Rt△ABD和Rt△ACD.你能在 哪一个三角形中求出AD呢? A B C D 北 东 在Rt△ACD中,只知道∠CAD=25°, 不能求AD. 在Rt△ABD中,知道 ∠BAD=55°,虽然知道 BC=20海里,但它不是 Rt△ABD的边,也不能求出AD. 这两个三角形有联系,AD 是它们的公共直角边.而 且BC是这两个直角三角 形BD与CD的差,即BC= BD-CD.BD,CD的对角 是已知的,BD,CD和边 AD都有联系. (6)那该怎么做呢?是不是可以将它们结合起来,站在一个 更高的角度考虑? A B C D 北 东 在Rt△ABD中, , 在Rt△ACD中, 利用BC=BD-CD就可以列出关于 AD的一元一次方程,即 ADtan 55°-ADtan 25°=20. tan 55 BD AD = tan55 .BD AD = tan25 ,CD AD= tan25 .CD AD = (7)有何联系呢? A B C D 北 东 w解:过点A作AD⊥BC交BC延长线于点D, 根据题意可 知,∠BAD=55°,∠CAD=25°,BC= 20海里.设AD=x,则 答:货轮继续向东航行途中没有触礁的危险. D ┌ A B C D 北 东tan55 ,tan25 ,Q BD CD x x = = tan55 , tan 25 .BD x CD x = = 55° 25° tan55 tan25 20.x x - = 20 20 20.67tan55 tan25 1.4281 0.4663x = ≈ ≈ (海里). 因为AD>10海里,所以无触礁的危险. w如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为 30°,再往塔的方向前进50 m至B处,测得仰角为60°,那么该塔 有多高?(小明的身高忽略不计,结果精确到1 m). w要解决这问题,我们仍需将其数 学化. w请与同伴交流你是怎么想的? 准备怎么去做? w现在你能完成这个任务吗? 2.合作探究,理解新知 这个图形与前面的图形相同,因此解答如下: D A B C ┌ 50 m 30° 60° tan ,tan ,AC BCADC BDCx x Q tan60 , tan 30 .AC x BC x tan60 tan30 50.x x 50 50 25 3 43 m .tan60 tan30 33 3 x 答:该塔约有43 m高. 解:如图,根据题意可知,∠A=30°,∠DBC=60°, AB=50 m.设CD=x,则∠ADC=60°, ∠BDC=30°, w某商场准备改善原有楼梯的安全性能,把倾 角由原来的40°减至35°,已知原楼梯的长 度为4 m,调整后的楼梯会加长多少?楼梯多 占多长一段地面?(结果精确到0.01 m). w现在你能完成这个任务吗? w请与同伴交流你是怎么想的? 准备怎 么去做? A B CD ┌ 课堂练习,巩固新知 w解:如图,根据题意可知,∠A=35°,∠BDC=40°,DB=4 m.求 (1)AB-BD的长,(2)AD的长. A B CD ┌ 4 m 35° 40° sin40 ,BC BD Q = sin40 .BC BD = sin35 ,BC AB Q = 答:调整后的楼梯会加长约0.48 m. sin45 4 0.6428 4.48 m .sin35 sin35 0.5736 BC BDAB = = ≈ ≈ 4.48 4 0.48 m .AB BD - ≈ - = w解:如图,根据题意可知,∠A=35°∠BDC=40°,DB=4m.求(2) AD的长. A B CD ┌ 4 m 35° 40° tan40 ,Q BC DC = .tan40 BCDC = tan35 ,BC AC =Q 答:楼梯多占约0.61 m一段地面. .tan35 BCAC = AD AC DC = 1 1 tan 35 tan40BC = - 1 1sin40 tan 35 tan40BD = - 0.61 m .≈ 1.钢缆长几何 w如图,一灯柱AB被一钢缆CD固定.CD与地面成40°夹角, 且DB=5 m.现再在CD上方2 m处加固另一根钢缆ED,那么, 钢缆ED的长度为多少?(结果精确到0.01 m). E B C D 2 m 40° 5 m 课堂练习,检测新知 w解:如图,根据题意可知,∠CDB=40°,EC=2 m,DB=5 m.求 DE的长. E B C D 2 m 40° 5 m tan40 ,BC BD =Q cos51.12 ,Q DB DE = w答:钢缆ED的长度约为7.97m. tan40 .BC BD = 2 tan40 2 6.1955 m .BE BC BD = + = + ≈ ( ) 5tan40 2tan 1.24.5 BEBDE BD += = ≈Q 5 7.97 m .cos51.12 0.6277 DBDE = = ≈ 51.12BDE ≈ . 2.大坝中的数学计 算 w如图,水库大坝的截面是梯形ABCD,坝顶AD=6 m,坡长 CD=8 m.坡底BC=30 m,∠ADC=135°. w(1)求坡角∠ABC的大小; w(2)如果坝长100 m,那么修建这个大坝共需多少土石方 (结果精确到0.01 m3 ). w解:如图,(1)求坡角∠ABC的大小; 过点D作DE⊥BC于点E,过点A作AF⊥BC于点F. tan45 4 2,EC DE DC = = = 答:坡角∠ABC约为13°. 4 2, 30 4 2.AF DE BF = = = - 4 2tan 0.2324. 30 4 2 AFABC BF = = ≈Q 13 .ABC ≈ w解:如图,(2)如果坝长100 m, 那么修建这个大坝共需多少土 石方(结果精确到0.01 m3 ). ,2 AD BC AFS += 答:修建这个大坝共需土石方约10 182.34 m3. 36 4 2 72 2.2S ×= = 3100 100 72 2 10182.34 m .V S = = × ≈ 如图,20海里/时的速度将一批重要物资由A处运往正西 方向的B处,经16小时的航行到达,到达后必须立即卸货. 此时.接到气象部门通知,一台风中心正以40海里/时的速 度由A向北偏西60°方向移动,距台风中200海里的圆形区 域(包括边界)均受到影响. (1)问:B处是否会受到台风的影响? 请说明理由. (2)为避免受到台风的影响,该船应在 多少小时内卸完货物? (供选用数据: ) 2 1.4, 3 1.7 拓展延伸,升华知识 解:(1)过点B作BD⊥AC.垂足为D. 依题意,得∠BAC=30°,在 Rt△ABD中, ∴B处会受到台风影响. (2)以点B为圆心,200海里为半径画圆交AC于E,F,由勾股 定理可求得DE=120, ∴ (小时). 因此,该船应在3.8小时内卸完货物. 1 1 20 16 160 200,2 2BD AB = = × × = 160 3.AD = 160 3 120.AE AD DE= - = - 160 3 120 3.840 - ≈ 利用解直角三角形的知识解决实际问题的一般步骤: 1.将实际问题抽象为数学问题; (画出平面图形,转化为解直角三角形的问题) 2.根据条件的特点,适当选用锐角三角函数等 去解直角三角形; 3.得到数学问题的答案; 4.得到实际问题的答案. (有“弦”用“弦”; 无“弦”用“切”) 课堂小结查看更多