- 2021-05-24 发布 |
- 37.5 KB |
- 11页


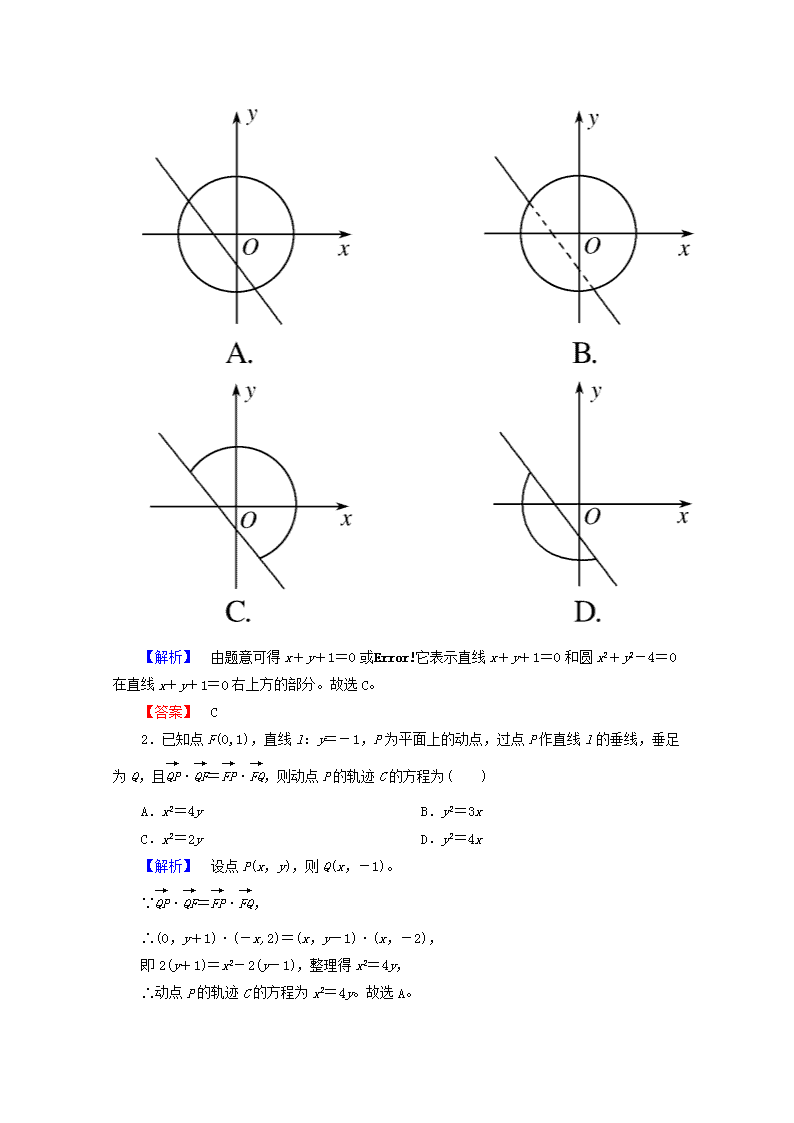
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2018届一轮复习北师大版第八章解析几何第八节曲线与方程教案
第八节 曲线与方程 ☆☆☆2017考纲考题考情☆☆☆ 考纲要求 真题举例 命题角度 1.了解方程的曲线与曲线的方程的对应关系; 2.了解解析几何的基本思想和利用坐标法研究几何问题的基本方法; 3.能够根据所给条件选择适当的方法求曲线的轨迹方程。 2016,全国卷Ⅲ,21,12分(求轨迹方程) 2015,湖北卷,21(1),5分(求曲线方程) 2015,全国卷Ⅰ,20(1),5分(求曲线方程) 2013,全国卷Ⅰ,10,5分(求曲线方程) 曲线与方程一般在客观题中主要考查圆的方程、椭圆方程、双曲线方程、抛物线方程,以考查待定系数法和定义法为主;在主观题中往往仅作为某一问的形式出现,重点结合圆锥曲线的其他性质进行综合考查。 微知识 小题练 自|主|排|查 1.曲线与方程的定义 一般地,在直角坐标系中,如果某曲线C上的点与一个二元方程f(x,y)=0的实数解建立了如下的对应关系: (1)曲线C上点的坐标都是这个方程的解; (2)以这个方程的解为坐标的点都是曲线上的点,那么,这个方程叫做曲线的方程,这条曲线叫做方程的曲线。 2.求动点的轨迹方程的基本步骤 (1)建系:建立适当的平面直角坐标系; (2)设点:轨迹上的任意一点一般设为P(x,y); (3)列式:列出或找出动点P满足的等式; (4)代换:将得到的等式转化为关于x,y的方程; (5)验证:验证所求方程即为所求的轨迹方程。 3.曲线的交点与方程组的关系 (1)两条曲线交点的坐标是两个曲线方程的公共解,即两个曲线方程组成的方程组的实数解; (2)方程组有几组解,两条曲线就有几个交点;方程组无解,两条曲线就没有交点。 微点提醒 1.求轨迹方程时,要注意曲线上的点与方程的解是一一对应关系。检验可从以下两个方面进行:一是方程的化简是否是同解变形;二是是否符合题目的实际意义。 2.求点的轨迹与轨迹方程是不同的要求,求轨迹时,应先求轨迹方程,然后根据方程说明轨迹的形状、位置、大小等。 3.求轨迹问题常用的数学思想 (1)函数与方程思想:求平面曲线的轨迹方程就是将几何条件(性质)表示为动点坐标x,y的方程及函数关系。 (2)数形结合思想:由曲线的几何性质求曲线方程是“数”与“形”的有机结合。 (3)等价转化思想:通过坐标系使“数”与“形”相互结合,在解决问题时又需要相互转化。 小|题|快|练 一 、走进教材 1.(必修2P124B组T1改编)等腰三角形ABC,若一腰的两个端点坐标分别是A(4,2),B(-2,0),A是顶点,则另一个点C的轨迹方程为( ) A.x2+y2-8x-4y=0 B.x2+y2-8x-4y-20=0(x≠10,x≠-2) C.x2+y2+8x+4y-20=0(x≠10,x≠-2) D.x2+y2-8x-4y+20=0(x≠10,x≠-2) 【解析】 设另一个点的坐标为C(x,y),则(x-4)2+(y-2)2=40,x≠10,x≠-2。整理得x2+y2-8x-4y-20=0(x≠10,x≠-2)。故选B。 【答案】 B 2.(选修2-1P36例3改编)若点P到直线x=-1的距离比它到点(2,0)的距离小1,则点P的轨迹为( ) A.圆 B.椭圆 C.双曲线 D.抛物线 【解析】 依题意,点P到直线x=-2的距离等于它到点(2,0)的距离,故点P的轨迹是抛物线。故选D。 【答案】 D 二、双基查验 1.方程(x2+y2-4)=0的曲线形状是( ) 【解析】 由题意可得x+y+1=0或它表示直线x+y+1=0和圆x2+y2-4=0在直线x+y+1=0右上方的部分。故选C。 【答案】 C 2.已知点F(0,1),直线l:y=-1,P为平面上的动点,过点P作直线l的垂线,垂足为Q,且·=·,则动点P的轨迹C的方程为( ) A.x2=4y B.y2=3x C.x2=2y D.y2=4x 【解析】 设点P(x,y),则Q(x,-1)。 ∵·=·, ∴(0,y+1)·(-x,2)=(x,y-1)·(x,-2), 即2(y+1)=x2-2(y-1),整理得x2=4y, ∴动点P的轨迹C的方程为x2=4y。故选A。 【答案】 A 3.和点O(0,0),A(c,0)距离的平方和为常数c的点的轨迹方程为________。 【解析】 设点的坐标为(x,y),由题意知 ()2+()2=c, 即x2+y2+(x-c)2+y2=c, 即2x2+2y2-2cx+c2-c=0。 【答案】 2x2+2y2-2cx+c2-c=0 4.MA和MB分别是动点M(x,y),与两定点A(-1,0)和B(1,0)的连线,则使∠AMB为直角的动点M的轨迹方程是________。 【解析】 点M在以A、B为直径的圆上,但不能是A、B两点。 【答案】 x2+y2=1(x≠±1) 5.已知圆的方程为x2+y2=4,若抛物线过点A(-1,0),B(1,0)且以圆的切线为准线,则抛物线的焦点轨迹方程是________。 【解析】 设抛物线焦点为F,过A,B,O作准线的垂线AA1,BB1,OO1,则|AA1|+|BB1|=2|OO1|=4,由抛物线定义得|AA1|+|BB1|=|FA|+|FB|, ∴|FA|+|FB|=4,故F点的轨迹是以A,B为焦点,长轴长为4的椭圆(去掉长轴两端点)。 【答案】 +=1(y≠0) 微考点 大课堂 考点一 直接法求轨迹方程 【典例1】 已知动圆过定点A(4,0),且在y轴上截得的弦MN的长为8。 (1)求动圆圆心的轨迹C的方程; (2)已知点B(-1,0),设不垂直于x轴的直线l与轨迹C交于不同的两点P,Q,若x轴是∠PBQ的角平分线,证明直线l过定点。 【解析】 (1)如图,设动圆圆心O1(x,y), 由题意,|O1A|=|O1M|, 当O1不在y轴上时, 过O1作O1H⊥MN交MN于H,则H是MN的中点, ∴|O1M|=, 又∵|O1A|=, ∴=, 化简得y2=8x(x≠0)。 又当O1在y轴上时,O1与O重合,点O1的坐标(0,0)也满足方程y2=8x, ∴动圆圆心的轨迹C的方程为y2=8x。 (2)证明:由题意,设直线l的方程为y=kx+b(k≠0), P(x1,y1),Q(x2,y2), 将y=kx+b代入y2=8x中,得k2x2+(2bk-8)x+b2=0, 其中Δ=-32kb+64>0。 由韦达定理得,x1+x2=,① x1x2=,② 因为x轴是∠PBQ的角平分线, 所以=-, 即y1(x2+1)+y2(x1+1)=0, (kx1+b)(x2+1)+(kx2+b)(x1+1)=0, 2kx1x2+(b+k)(x1+x2)+2b=0,③ 把①②代入③得2kb2+(k+b)(8-2bk)+2k2b=0, ∴k=-b,此时Δ>0,∴直线l的方程为y=k(x-1),即直线l过定点(1,0)。 【答案】 (1)y2=8x (2)直线l过定点(1,0),证明见解析 反思归纳 1.利用直接法求解轨迹方程的关键是根据条件准确列出方程,然后进行化简。 2.运用直接法应注意的问题 (1)在用直接法求轨迹方程时,在化简的过程中,有时破坏了方程的同解性,此时就要补上遗漏的点或删除多余的点,这是不能忽视的。 (2)若方程的化简过程是恒等变形,则最后的验证可以省略。 【变式训练】 已知点O(0,0),A(1,2),动点P满足|+|=2,则P点的轨迹方程是( ) A.4x2+4y2-4x-8y+1=0 B.4x2+4y2-4x-8y-1=0 C.8x2+8y2+2x+4y-5=0 D.8x2+8y2-2x+4y-5=0 【解析】 设P点的坐标(x,y),则=(x,y),=(x-1,y-2),+=(2x-1,2y-2)。所以(2x-1)2+(2y-2)2=4,整理得4x2+4y2-4x-8y+1=0。故选A。 【答案】 A 考点二 定义法求轨迹方程 【典例2】 已知圆C与两圆x2+(y+4)2=1,x2+(y-2)2=1外切,圆C的圆心轨迹为L,设L上的点与点M(x,y)的距离的最小值为m,点F(0,1)与点M(x,y)的距离为n。 (1)求圆C的圆心轨迹L的方程; (2)求满足条件m=n的点M的轨迹Q的方程。 【解析】 (1)两圆半径都为1,两圆圆心分别为C1(0,-4),C2(0,2),由题意得|CC1|=|CC2|,可知圆心C的轨迹是线段C1C2的垂直平分线,C1C2的中点为(0,-1),直线C1C2 的斜率不存在,故圆心C的轨迹是线段C1C2的垂直平分线,其方程为y=-1,即圆C的圆心轨迹L的方程为y=-1。 (2)因为m=n,所以M(x,y)到直线y=-1的距离与到点F(0,1)的距离相等,故点M的轨迹Q是以y=-1为准线,点F(0,1)为焦点,顶点在原点的抛物线,而=1,即p=2,所以,轨迹Q的方程是x2=4y。 【答案】 (1)y=-1 (2)x2=4y 反思归纳 1.定义法求轨迹方程的适用条件:动点与定点、定直线之间的某些关系满足直线、圆、椭圆、双曲线、抛物线的定义。 2.定义法求轨迹方程的关键是理解平面几何图形的定义。 【变式训练】 在△ABC中,A为动点,B,C为定点,B,C(a>0),且满足条件sinC-sinB=sinA,则动点A的轨迹方程是________。 【解析】 由正弦定理,得-=×(R为外接圆半径), 所以|AB|-|AC|=|BC|,即点A的轨迹是以B、C为焦点的双曲线的右支(不含右顶点)。又知实轴长为a,焦距为a, ∴虚半轴长为 ,∴动点A的轨迹方程为-=1(x>0且y≠0)。 【答案】 -=1(x>0且y≠0) 考点三 代入法(相关点法)求轨迹方程 【典例3】 在圆x2+y2=4上任取一点P,设点P在x轴上的正投影为点D。当点P在圆上运动时,动点M满足=2,动点M形成的轨迹为曲线C。 (1)求曲线C的方程; (2)已知点E(1,0),若A,B是曲线C上的两个动点,且满足EA⊥EB,求·的取值范围。 【解析】 (1)解法一:由=2知点M为线段PD的中点, 设点M的坐标是(x,y),则点P的坐标是(x,2y)。 因为点P在圆x2+y2=4上, 所以x2+(2y)2=4。 所以曲线C的方程为+y2=1。 解法二:设点M的坐标是(x,y),点P的坐标是(x0,y0), 由=2,得x0=x,y0=2y。 因为点P(x0,y0)在圆x2+y2=4上, 所以x+y=4。① 把x0=x,y0=2y代入方程①,得x2+4y2=4。 所以曲线C的方程为+y2=1。 (2)因为EA⊥EB,所以·=0。 所以·=·(-)=2。 设点A(x1,y1),则+y=1,即y=1-。 所以·=2=(x1-1)2+y=x-2x1+1+1-=x-2x1+2=2+。 因为点A(x1,y1)在曲线C上,所以-2≤x1≤2。 所以≤2+≤9。 所以·的取值范围为。 【答案】 (1)+y2=1 (2) 反思归纳 代入法求轨迹方程的关键是寻找所求动点与已知动点间的等量关系。常涉及中点问题、三角形重心问题及向量相等或向量间关系等知识。 【变式训练】 已知F1,F2分别为椭圆C:+=1的左、右焦点,点P为椭圆C上的动点,则△PF1F2的重心G的轨迹方程为( ) A.+=1(y≠0) B.+y2=1(y≠0) C.+3y2=1(y≠0) D.x2+=1(y≠0) 【解析】 依题意知F1(-1,0),F2(1,0), 设P(x0,y0),G(x,y), 则由三角形重心坐标关系可得 即 代入+=1得重心G的轨迹方程为+3y2=1(y≠0)。故选C。 【答案】 C 微考场 新提升 1.平面上动点P到定点F与定直线l的距离相等,且点F与直线l的距离为1。某同学建立直角坐标系后,得到点P的轨迹方程为x2=2y-1,则他的建系方式是( ) 解析 因为点P的轨迹方程为x2=2y-1, 即所求的抛物线方程为y=x2+, 抛物线的对称轴为y轴,顶点坐标为。 所以该同学的建系方式是C。 答案 C 2.若曲线C上存在点M,使M到平面内两点A(-5,0),B(5,0)距离之差的绝对值为8,则称曲线C为“好曲线”。以下曲线不是“好曲线”的是( ) A.x+y=5 B.x2+y2=9 C.+=1 D.x2=16y 解析 ∵M到平面内两点A(-5,0),B(5,0)距离之差的绝对值为8,∴M的轨迹是以A(-5,0),B(5,0)为焦点的双曲线,方程为-=1。 A项,直线x+y=5过点(5,0),故直线与M的轨迹有交点,满足题意; B项,x2+y2=9的圆心为(0,0),半径为3,与M的轨迹没有交点,不满足题意; C项,+=1的右顶点为(5,0),故椭圆+=1与M的轨迹有交点,满足题意; D项,方程代入-=1,可得y-=1,即y2-9y+9=0,∴Δ>0,满足题意。故选B。 答案 B 3.(2016·天津模拟)在平面直角坐标系中,已知两点A(3,1),B(-1,3),若点C满足=λ1+λ2(O为原点),其中λ1,λ2∈R,且λ1+λ2=1,则点C的轨迹是( ) A.直线 B.椭圆 C.圆 D.双曲线 解析 设C(x,y),因为=λ1+λ2,所以(x,y)=λ1(3,1)+λ2(-1,3),即解得又λ1+λ2=1,所以+=1,即x+2y=5,所以点C的轨迹为直线。故选A。 答案 A 4.(2017·衡水模拟)设过点P(x,y)的直线分别与x轴的正半轴和y轴的正半轴交于A,B两点,点Q与点P关于y轴对称,O为坐标原点,若=2且·=3,则点P的轨迹方程是( ) A.3x2+y2=1(x>0,y>0) B.+y2=1(x>0,y>0) C.-y2=1(x>0,y>0) D.x2+=1(x>0,y>0) 解析 由P(x,y),可知Q(-x,y)。设A(a,0),B(0,b),其中a>0,b>0,∴=(x,y-b),=(a-x,-y),由=2可得a=x,b=3y,∴x>0,y>0,又=(-a,b)=,·=(-x,y)·=x2+3y2=3,即+y2=1, ∴点P的轨迹方程为+y2=1(x>0,y>0)。故选B。 答案 B 5.(2016·临汾模拟)在△ABC中,||=4,△ABC的内切圆切BC于D点,且||-||=2,则顶点A的轨迹方程为________。 解析 如图,以BC的中点为原点,中垂线所在直线为y轴建立如图所示的平面直角坐标系,E,F分别为两个切点。 则|BE|=|BD|,|CD|=|CF|, |AE|=|AF|。 所以|AB|-|AC|=2, 所以点A的轨迹为以B,C为焦点的双曲线的右支(不含右顶点),且a=,c=2,所以b=, 所以轨迹方程为-=1(x>)。 答案 -=1(x>)(答案不唯一)查看更多