- 2021-02-26 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
河南省部分重点高中2019届高三3月联考数学(理)试卷(PDF版)
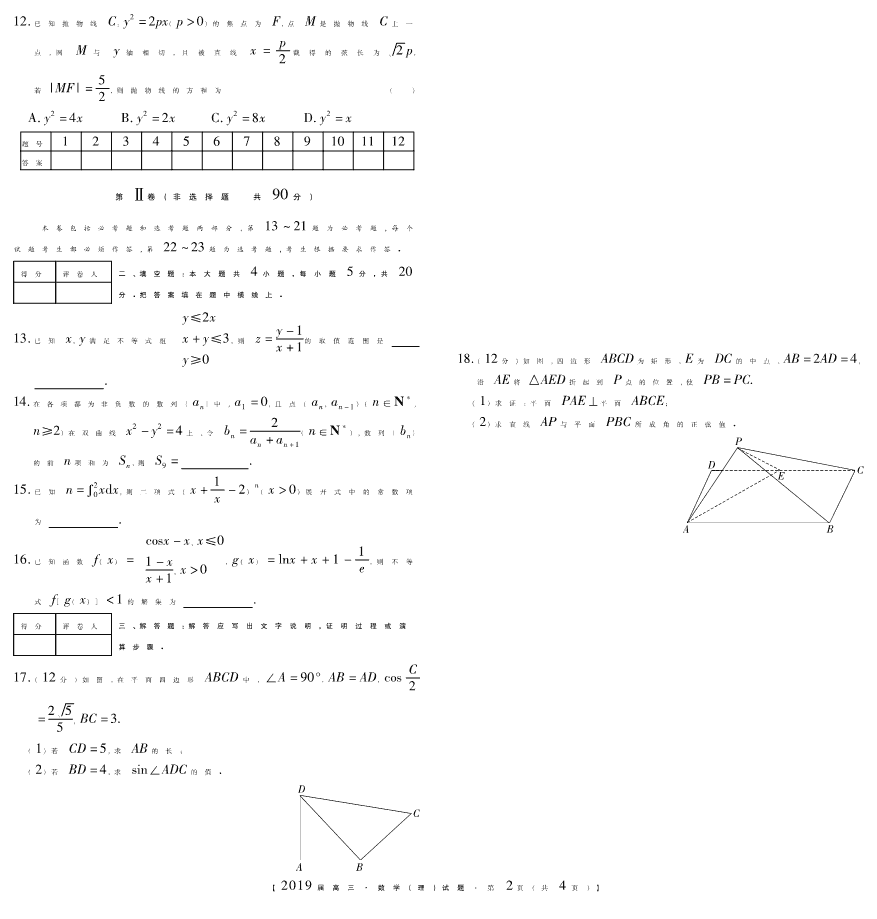
书书书 【2019届高三·数学(理)试题·第 1 页(共 4页)】 大 联 考 试 卷 数学(理) (试卷总分 150分 考试时间 120分钟) 题号 第Ⅰ卷 第Ⅱ卷 总分 合分人 复分人 得分 第Ⅰ卷(选择题 共 60分) 得分 评卷人 一、选择题:本大题共 12小题,每小题 5分,共 60 分.在每小题给出的四个选项中只有一项是符合 题目要求的. 1.已知集合 A={x∈Z|-1≤x<2},则满足条件 A∩B=B的集合 B 的个数为 ( ) A.4 B.7 C.3 D.8 2.已知复数 z=1-i,则 z2+|z|2在复平面上对应的点在 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 !"# $ !"# %&$ $ $"% '($ )"$$ &% *+$$ '% 3.国庆节期间,滕州市实验小学举行 了一次科普知识竞赛活动,设置了 一等奖、二等奖、三等奖、四等奖及 纪念奖,获奖人数的分配情况如图 所示,各个奖品的单价分别为:一 等奖 50元、二等奖 20元、三等奖 10元,四等奖 5元,纪念奖 2元,则以下说法中不正确 獉獉獉 的是 ( ) A.获纪念奖的人数最多 B.各个奖项中二等奖的总费用最高 C.购买奖品的费用平均数为 6.65元 D.购买奖品的费用中位数为 5元 4.若“p或 q”成立的充分条件是“瓙r”,则下列推理:①“p或 q”瓙r; ②瓙rp;③r瓙(p或 q);④瓙p且瓙qr.其中正确的个数是( ) A.1 B.2 C.3 D.4 5.已知 数 列 {an}为 等 比 数 列,且 a5 是 a3 与 a7 的 等 差 中 项, a2019=2018,则首项 a1= ( ) A.2019 B.±2018 C.2018 D.±2019 6.已知双曲线x2 a2 -y2 b2 =1(a>0,b>0)的左、右顶点为 A,B,点 P为双 曲线上异于 A,B的任意一点,设直线 PA,PB的斜率分别为 k1,k2, 若 k1k2=1 2,则双曲线的离心率为 ( ) A.槡3 2 B.2 C.槡6 2 D.3 2 7.设 a,b,c∈ N ,且 b<c,定 义 函 数 如 下: f(a+ b c) = a+1,(a是偶数) a-1,(a是奇数{ ) ,则 f(5-2019 2018)-f(4+2018 2019)= ( ) ! " ! " !"# $"% &"% A.1 B.-1 C.-3 D.0 8.如图,是某几何体的三视图,该几何体 的轴截面的面积为 6,则该几何体的外 接球的表面积为 ( ) A.65 3π B.65 4π C.65 12π D.33 4π ! " #$ % &9.如图,在平行四边形 ABCD中,E,F分 别是 BC,CD上的一点,且 →BE=1 3 →BC, →DF=2→FC,则 →AF+→DE= ( ) A.5 3 →AB-1 3 →AD 开始 !!" "!" #$%&"!'( "#")""#")! !#!)#$%*" ! 是偶数! 输出 "结束 是 是 否 否 B.5 3 →AB+5 3 →AD C.4 3 →AB-2 3 →AD D.5 3 →AB+1 3 →AD 10.执行如图所示的程序框图,输出的 结果为 ( ) A.1 B.2 C.3 D.4 !!"! #! $! !" $ # 11.如图,在长方体 ABCD-A1B1C1D1 中,对角线 DB1与平面 ADD1A1,ABCD,DCC1D1 的夹角分 别为 α,β,θ,且 DB1 槡=2 6,sinα+sinβ+sinθ= 槡2 6 3 ,则长方体的全面积为 ( ) A.40 B.64 C.20 D.8 【2019届高三·数学(理)试题·第 2 页(共 4页)】 12.已知抛物线 C:y2=2px(p>0)的焦点为 F,点 M是抛物线 C上一 点,圆 M 与 y轴 相 切,且 被 直 线 x= p 2截 得 的 弦 长 为 槡2p, 若|MF|=5 2,则抛物线的方程为 ( ) A.y2=4x B.y2=2x C.y2=8x D.y2=x 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 第Ⅱ卷(非选择题 共 90分) 本卷包括必考题和选考题两部分,第 13~21题为必考题,每个 试题考生都必须作答,第 22~23题为选考题,考生根据要求作答. 得分 评卷人 二、填空题:本大题共 4小题,每小题 5分,共 20 分.把答案填在题中横线上. 13.已知 x,y满足不等式组 y≤2x x+y≤3 y≥{ 0 ,则 z=y-1 x+1的取值范围是 . 14.在各项都为非负数的数列{an}中,a1 =0,且点(an,an-1)(n∈N, n≥2)在双曲线 x2-y2=4上,令 bn= 2 an+an+1 (n∈N ),数列{bn} 的前 n项和为 Sn,则 S9= . 15.已知 n=2 0xdx,则二项式(x+1 x-2)n(x>0)展开式中的常数项 为 . 16.已知函数 f(x)= cosx-x,x≤0 1-x x+1,x{ >0 ,g(x)=lnx+x+1-1 e,则不等 式 f[g(x)]<1的解集为 . 得分 评卷人 三、解答题:解答应写出文字说明,证明过程或演 算步骤. 17.(12分)如图,在平面四边形 ABCD中,∠A=90°,AB=AD,cosC 2 = 槡2 5 5 ,BC=3. (1)若 CD=5,求 AB的长; (2)若 BD=4,求 sin∠ADC的值. ! " # $ 18.(12分)如图,四边形 ABCD为矩形,E为 DC的中点,AB=2AD=4, 沿 AE将△AED折起到 P点的位置,使 PB=PC. (1)求证:平面 PAE⊥平面 ABCE; (2)求直线 AP与平面 PBC所成角的正弦值. ! " #$ % & 【2019届高三·数学(理)试题·第 3 页(共 4页)】 19.(12分)已 知 椭 圆 C:x2 a2 +y2 b2 =1(a>b>0)的 左、右 焦 点 为 F1,F2,点 P是椭圆上异于左、右顶点的任意一点,O为原点,过右 焦点 F2作∠F1PF2的外角平分线 l的垂线,垂足为 Q,且|OQ|=2, 椭圆的离心率为 1 2. (1)求椭圆 C的方程; (2)设 S是圆 x2 +y2 =7上任一点,由 S引椭圆两条切线 SA,SB, 切点分别为 A,B,求证:SA⊥SB. 20.(12分)滕州市公交公司一切为了市民着想,为方便市区学生的 上下学,专门开通了学生公交专线,在学生上学、放学的时间段运 行,为了更好地掌握发车间隔时间,公司工作人员对滕州二中车 站发车间隔时间与侯车人数之间的关系进行了调查研究,现得到 如下数据: 间隔时间 x(分钟) 10 11 13 12 15 14 侯车人数 y(人) 23 25 29 26 31 28 调查小组确定的研究方案是:先从这六组数据中选取 2组,用剩下 的 4组数据求线性回归方程,再用被选取的 2组数据进行检验; (1)从中任选 2组数据,设 X为候车时间不超过 11分钟的数据组 的个数,求随机变量 X的分布列; (2)若选取的是前两组数据,请根据后四组数据,求出 y关于 x的 线性回归方程 ) y= ) bx+ ) a; (3)若由线性回归方程得到的估计数据与所选出的检验数据的误 差均不超过 1人,则称为最佳回归方程,在(2)中求出的回归 方程是否是最佳回归方程?若规定一辆公交车的载客人数不 超过 35人,则间隔时间设置为 18分钟,是否合适? 参考公式:,) b= ∑ n i=1 xiyi-nxy ∑ n i=1 x2 i-nx2 = ∑ n i=1 (xi-x)(yi-y) ∑ n i=1 (xi-x)2 ,) a=y- ) bx. 【2019届高三·数学(理)试题·第 4 页(共 4页)】 21.(12分)已知函数 f(x)=lnx-1,g(x)=ax,a∈R. (1)若函数 y=f(x)+g(x)在(0,e]上单调递增,求实数 a的取值 范围; (2)当 a=1时,令 h(x)=exf(x)+g(x),是否存在实数 x0∈(0,+∞), 使曲线 y=h(x)在点(x0,h(x0))处的切线与曲线 H(x)= x-ex+1 ex的一条切线垂直?若存在,求出 x0 的值;若不存 在,请说明理由. 请考生在第 22、23题中任选一题作答,如果多做,则按所做的第 一题计分. 22.(10分)【选修 4-4 坐标系与参数方程】 在平面直角坐标系 xOy中,直线 l的参数方程为 x=-2+tcosα y=tsin{ α (t为 参数),以坐标原点 O为极点,x轴的正半轴为极轴建立极坐标系,圆 C的极坐标方程为 ρ=1. (1)若直线 l与圆 C相切,求 α的值; (2)直线 l与圆 C相交于不同两点 A,B,线段 AB的中点为 Q,求点 Q的轨迹的参数方程. 23.(10分)【选修 4-5 不等式选讲】 已知不等式|x+3|≥2a+b+c,a,b,c∈R. (1)当 2a+b=2,c=|x+1|时,解不等式|x+3|≥2a+b+c; (2)当 a2 +b2 +c2 =6时,不等式 |x+3|≥2a+b+c对所有实数 a,b,c都成立,求实数 x的取值范围. 你选做的题目是 题(填 22、23) 答案: 书书书 大联考·数学(理) 参考答案 1.D(解析:A={x∈Z|-1≤x<2}={-1,0,1}, ∵A∩B=B,∴BA,∵集合 A有 3个元素,∴其子 集有 8个,故选 D.) 2.D(解析:∵z=1-i,∴z2 +|z|2 =(1-i)2 + (槡2)2=2-2i,则 z2+|z|2 在复平面上对应的点在 第四象限,故选 D.) 3.B(解析:设参加竞赛的人数为 a人,由扇形统计 图可知,一等奖占 2%,二等奖占 8%,三等 奖 占 15%,四等奖占 35%,获得纪念奖的人数占 40%, 最多,A正确;各奖项的费用:一等奖 2%a×50=a, 二等奖 8% a×20=1.6a,三 等 奖 15% a×10= 1.5a,四等奖 35%a×5=1.75a,纪念奖 40%a×2 =0.8a,B错误;平均费用为 50×2%+20×8%+ 10×15%+5×35%+2×40%=6.65元,C正确; 由各个获奖的人数的比例知,购买奖品的费用的中 位数为 5元,D正确,故选 B.) 4.A(解析:由已知得,瓙rp或 q,它的逆否命题④ 为真,不正确的序号是①②③,故选 A.) 5.C(解析:设数列{an}的公比为 q,∵a5是 a3与 a7 的等差中项,∴2a5=a3+a7,即 2a1q4=a1q2+a1q6, ∴q4-2q2+1=0,解得,q=±1,则 a2019 =a1q2018 = a1(±1)2018=a1=2018,故选 C.) 6.C(解析:由题设知,A(-a,0),B(a,0),设 P(x,y), 则 k1= y x+a,k2 = y x-a,∴k1k2 = y x+a× y x-a= y2 x2-a2 =1 2,∵P(x,y)点在双曲线上,∴y2=b2 a2(x2-a2),则 b2 a2(x2-a2) x2-a2 =1 2,化简得,2b2 =a2,又 b2 =c2 -a2, ∴2c2=3a2,则 e=槡6 2,故选 C.) 7.C(解析:由题意知,f(5-2019 2018)-f(4+2018 2019)= f(3+2017 2018)-f(4+2018 2019)=(3-1)-(4+1)=-3, 故选 C.) 8.B(解析:由三视图知,该几何体是一个圆台,圆 台的上底半径为 1,下底半径为 2,设圆台的高为 h, 则轴截面的面积为 S=(2+4)h 2 =6,∴h=2,设圆 台的外接球的半径为 R,则由题意得, R2-1槡 2 + R2-2槡 2 =2,解 得,R2 =65 16,(或 R2-1槡 2 - R2-2槡 2 =2,此时无解),∴外接球的表面积为: S=4πR2=65π 4 ,故选 B.) 9.D(解析:∵四边形 ABCD是平行四边形,且 →DF= 2→FC,∴ →AF=→AD+→DF=→AD+2 3 →DC=→AD+2 3 →AB,又 →BE=1 3 →BC,∴ →DE=→DC+→CE=→AB+2 3 →CB=→AB- 2 3 →AD,则 →AF+ →DE=→AB-2 3 →AD+ →AD+2 3 →AB= 5 3 →AB+1 3 →AD,故选 D.) 10.D(解析:由程序框图知,k=1,x=1log2x=0, 否x=1+1=2,log2x=1>0,是x=2+1=3, k=1+log33=2,是x=1log2x=0,否x=1+1 =2,log2x=1>0,是x=2+2=4,k=2+log34, 否,输出 x=4,故选 D.) 11.A(解析:连结 DA1,DB,DC1,由长方体的性质 知,∠A1DB1 =α,∠BDB1 =β,∠C1DB1 =θ,∴sinα + sinβ + sinθ = A1B1 DB1 + BB1 DB1 + C1B1 DB1 = A1B1+BB1+C1B1 DB1 =A1B1+BB1+C1B1 槡2 6 = 槡2 6 3 ,则 A1B1 +BB1 +C1B1 =8,∴ A1B2 1 +BB2 1 +C1B2 1 + 2(A1B1·BB1+BB1·C1B1 +A1B1·C1B1)=64,即 DB2 1+S全 =64,∴S全 =40,故选 A.) ! " # $ % & ' ( 12.A(解析:设圆 M与 y轴切 于点 N,直线 x=p 2与圆 M交 于 A,B两 点,如 图 所 示,设 M(x0,y0),则|MN|=|MA|= |MB|=x0,|AB 槡|= 2p, ∴(槡2 2p)2 +(x0 -p 2)2 =x2 0, 解得,x0=3 4p,由抛物线的定义知,|MF|=x0 +p 2, ∵|MF|=5 2,∴ 5 2=3 4p+1 2p,即 p=2,∴抛物线 的方程为 y2=4x,故选 A.) ! " # !$"!" "!#! %!$"## &!%$"$$ 13.[-1,1 2](解析:作出 不等式组 y≤2x x+y≤3 y≥{ 0 所表示 的平面区域,如图所示,z= y-1 x+1的最大值即为直线 BA 的斜率 1 2,最小值为直线 BO的斜率 -1,故取值范 围是[-1,1 2].) 14.3(解析:∵点(an,an-1)(n∈N ,n≥2)在双曲 线 x2 -y2 =4上,∴ a2 n -a2 n-1 =4,又 a1 =0, ∴数列{a2 n}是以 0为首项,以 4为公差的等差数 列,则 a2 n =4(n-1),又 an≥0,∴an =2 n槡 -1, 则 bn= 2 an+an+1 = 2 2 n槡 -1+2槡n = 1 n槡 -1+槡n = 槡n- n槡 -1,∴S9=b1+b2+… +b9 槡 槡= 1-0+ 2- 槡1+… 槡 槡+ 9- 8=3.) 15.6(解 析:∵ n = 2 0xdx = 1 2 x2 |2 0 = 2, ∴(x+1 x-2)n=(x+1 x-2)2=(槡x-1 槡x )4,其通项 为 Tr+1=Cr 4(槡x)4-r(-1 槡x )r=(-1)rCr 4x2-r,令 2-r =0,则 r=2,∴展开式的常数项为(-1)2C2 4=6.) ! " # $ "!"#!$% %"!&!$ 16.(1 e,+∞)(解析: ∵f(x)= cosx-x,x≤0 1-x x+1,x{ >0 , ∴f′(x) = -sinx-1,x≤0 -2 (x+1)2,x{ >0, 则 f′(x)≤0,∴f(x)在 R上单调递减,又 f(0)=1, ∴不 等 式 f[g(x)]<1即 为 f[g(x)]<f(0), 则 g(x)>0,即 lnx+x+1-1 e>0,∴lnx+1>-x +1 e,由函数 y=lnx+1和 y=-x+1 e的图象知, 当 x>1 e时,不等式成立,故不等式 f[g(x)]<1的 解集为(1 e,+∞).) 17.解:(1)∵cosC 2= 槡2 5 5 , ∴cosC=2cos2 C 2-1=2×( 槡2 5 5 )2-1=3 5, (2分) !! !!!!!!!!!!!!!!!! ∵BC=3,CD=5, ∴由余弦定理得,BD2 =BC2 +CD2 -2BC·CDcosC =32+52-2×3×5×3 5=16,则 BD=4, ∵∠A=90°,AB=AD,∴AB=槡2 2BD 槡=2 2; (6分) !!! !!!!!!!!!!!!!!!! (2)由(1)知,sinC=4 5, ∵BC=3,BD=4, ∴由正弦定理得, sin∠BDC=BC·sinC BD = 3×4 5 4 =3 5, (9分)!!! ∵BC<BD,∴cos<BDC=4 5, ∵∠A=90°,AB=AD,∴∠ADB=45°, 则 sin∠ADC=sin(∠BDC+45°) =sin∠BDCcos45°+cos∠BDCsin45° =3 5×槡2 2+4 5×槡2 2= 槡7 2 10. (12分)!!!!!! 18.(1)证明:如图,取 AE的中点 O,BC的中点 F, 连结 OP,OF,PF,则 OF∥AB, ∴OF⊥BC,∵PB=PC,∴PF⊥BC, 又 OF∩PF=F,∴BC⊥平面 POF,则 BC⊥PO, (3分) ! !!!!!!!!!!!!!!!! ∵E为 DC的中点,AB=2AD=4, ∴PA=PE,则 PO⊥AE, ∵AE,BC是平面 ABCE的相交直线, ∴PO⊥平面 ABCE, 又 PO平面 PAE, ∴平面 PAE⊥平面 ABCE; (5分)!!!!!!! (2)解:在平面 ABCE内,过点 O作 Ox⊥OF,则以 O 为原点,以 Ox,OF,OP分别为 x,y,z轴,建立空间 直角坐标系,如图所示, ! " # $ %& ' ( ) * + 由题设知,A(1,-1,0),P(0,0,槡2), B(1,3,0),C(-1,3,0), ∴ →PB=(1,3, 槡- 2),→PC=(-1,3, 槡- 2), (8分) !!! !!!!!!!!!!!!!!!! 设平面 PBC的法向量为 n=(x,y,z), 由 n· →PB=(x,y,z)·(1,3, 槡- 2)=0 n· →PC=(x,y,z)·(-1,3, 槡- 2){ =0 得,x+3y 槡- 2z=0 -x+3y 槡- 2z{ =0 ,取 z 槡= 2,则 x=0,y=2 3, ∴平面 PBC的一个法向量为 n=(0,2 3,槡2), (10分) ! !!!!!!!!!!!!!!!! 设直线 AP与平面 PBC所成角为 θ, ∵ →AP=(-1,1,槡2), ∴sinθ=|cos<n,→AP>|=| n· →AP |n|·|→AP|| =| 2 3+2 4 9+2· 槡槡 1+1+2 |= 槡2 22 11 , 即直线 AP与平面 PBC所成角的正弦值为 槡2 22 11 . (12分)!!!!!!!!!!!!!!!! 19.(1)解:延长 F2Q交直线 F1P于点 R, 由题设知,|PF2|=|PR|,且 Q为 F2R的中点, ∴|OQ|=1 2|F1R|=1 2(|PF1|+|PR|) =1 2(|PF1|+|PF2|)=1 2×2a=a=2, (2分) !!!! !!!!!!!!!!!!!!!! 又 e=c a=1 2,∴c=1,则 b 槡= 3, 故椭圆 C的方程为x2 4+y2 3=1; (4分)!!!!! (2)证明:当两条切线中的一条的斜率不存在时, 不妨设点 S在第一象限且 SA⊥x轴, 则点 A为椭圆的右顶点,∴A(2,0), ∵点 S在圆 x2+y2=7上,∴S(2,槡3), 此时,B(0,槡3)为椭圆的上顶点,∴SA⊥SB; (6分) !! !!!!!!!!!!!!!!!! 当两条切线的斜率都存在时,设 S(x0,y0),一条切 线的斜率为 k, 则过点 S的切线方程为 y-y0=k(x-x0), 联立 y-y0=k(x-x0) x2 4+y2 3{ =1 消去 y得, (3+4k2)x2+8k(y0-kx0)x+4(y0-kx0)2-12=0, ∵直线和椭圆相切, ∴Δ=64k2(y0-kx0)2-4(3+4k2)[4(y0 -kx0)2 - 12]=0, 即(x2 0-4)k2-2x0y0k+y2 0-3=0, (10分)!!! 则 kSA·kSB =y2 0-3 x2 0-4, ∵S在圆 x2+y2=7上,∴x2 0+y2 0=7, ∴kSA·kSB =7-x2 0-3 x2 0-4 =-1,故 SA⊥SB. (12分) !!!! !!!!!!!!!!!!!!!! 20.解:(1)由题设知,X=0,1,2, 则 P(X=0)=C2 4 C2 6 =2 5, P(X=1)=C1 2C1 4 C2 6 =8 15, P(X=2)=C2 2 C2 6 =1 15, (3分)!!!!!!!!! ∴随机变量 X的分布列为: X 0 1 2 P 2 5 8 15 1 15 (4分)!!!!!!!!!!!!!!!!!! (2)后四组数据是: 间隔时间 x(分钟) 13 12 15 14 侯车人数 y(人) 29 26 31 28 ∴x=13+12+15+14 4 =13.5, y=29+26+31+28 4 =28.5, 又∑ 4 i=1 xiyi=13×29+12×26+15×31+14×28= 1546, ∑ n i=1 x2 i=132+122+152+142=734, (7分)!!! ∴ ) b= ∑ n i=1 xiyi-nxy ∑ n i=1 x2 i-nx2 =1546-4×13.5×28.5 734-4×13.52 =1.4, 则 ) a=y- ) bx=28.5-1.4×13.5=9.6, ∴y关于 x的线性回归方程为 ) y=1.4x+9.6; (9分) ! !!!!!!!!!!!!!!!! (3)由(2)知,当 x=10时,) y=23.6, ∴|23.6-23|<1, 当 x=11时,) y=25,∴|25-25|<1, ∴求出的回归方程是最佳回归方程; 当 x=18时,) y=1.4×18+9.6=34.8, ∵34.8<35,∴间隔时间设置为 18分钟合适. (12分) ! !!!!!!!!!!!!!!!! 21.解:(1)由题设知, y=f(x)+g(x)=lnx-1+ax, 则 y′=1 x+a, ∵函数 y=f(x)+g(x)在(0,e]上单调递增, ∴y′=1 x+a≥0在(0,e]上恒成立, 即 a≥ -1 x在(0,e]上恒成立, ∵y=-1 x在(0,e]上单调递增, ∴a≥ -1 e; (4分)!!!!!!!!!!!!! (2)由题设知,h(x)=(lnx-1)ex+x, ∴h′(x)=(lnx-1)′ex+(lnx-1)(ex)′+1 =ex x+(lnx-1)ex+1=(1 x+lnx-1)ex+1; (6分) !! !!!!!!!!!!!!!!!! 设 m(x)=1 x+lnx-1,其定义域为(0,+∞), 则 m′(x)=-1 x2 +1 x=x-1 x2 ; 令 m′(x)=0,则 x=1, 当 0<x<1时,m′(x)<0, m(x)在(0,1)上单调递减; 当 x>1时,m′(x)>0, m(x)在(1,+∞)上单调递增; ∴在(0,+∞)上, m(x)min=m(1)=1+ln1-1=0, 即当 x∈(0,+∞)时,m(x)=1 x+lnx-1≥0; (9分) ! !!!!!!!!!!!!!!!! ∴当 x0∈(0,+∞)时,ex0 >1,1 x0 +lnx0-1≥0, ∴h′(x0)=(1 x0 +lnx0-1)ex0 +1≥1, 当且仅当 x0=1时取等号. 而对于 H(x),H′(x)=1-(ex+1 ex)≤ 1-2 ex-1 e槡 x =-1, 当且仅当 x=0时取得等号. ∴h′(x0)H′(x)≤ -1, 当且仅当 x0=1,x=0时取等号, 故存在 x0=1,使得结论成立. (12分)!!!!! 22.解:(1)∵圆 C的极坐标方程为 ρ=1, ∴C的直角坐标方程为 x2+y2=1, 圆心为(0,0),半径为 r=1; ∵直线 l过点 P(-2,0),倾斜角为 α, ∴当 α=π 2时,不合题意, (2分)!!!!!!! 当 α≠ π 2时,斜率为 k=tanα, 则直线的方程为 y=k(x+2), 即 kx-y+2k=0,∵直线 l与圆 C相切, ∴ |2k| k2槡 +1 =1,解得,k=±槡3 3, 即 tanα=±槡3 3,∴α=π 6或 α=5π 6; (5分)!!! (2)∵直线 l与圆 C相交于不同两点 A,B, ∴由(1)知,α∈[0,π 6)∪(5π 6,π), 设 A,B,Q对应的参数分别为 tA,tB,tQ, 则 tQ =tA+tB 2 , (7分)!!!!!!!!!!!! 将 x=-2+tcosα y=tsin{ α 代入 x2+y2=1得, t2-4tcosα+3=0, 则 tA+tB =4cosα,∴tQ =2cosα, 又点 Q的坐标(x,y)满足 x=-2+tQcosα y=tQsin{ α , 即 x=-2+2sin2α y=2cosαsin{ α , 故点 Q的轨迹的参数方程是 x=-1+cos2α y=sin2{ α (α为 参数,α∈[0,π 6)∪(5π 6,π)). (10分)!!!! 23.解:(1)当 2a+b=2,c=|x+1|时, 不等式|x+3|≥2a+b+c为|x+3|≥2+|x+1|, 当 x≤ -3时,-x-3≥2-x-1,-3≥1,无解; (2分) ! !!!!!!!!!!!!!!!! 当 -3<x<-1时,x+3≥2-x-1,x≥ -1,无解; 当 x≥ -1时,x+3≥2+x+1,3≥3,∴x≥ -1; 综上,不等式的解集为{x|x≥ -1}; (5分)!!! (2)由柯西不等式得, (2a+b+c)2≤(22+12+12)(a2+b2+c2), ∵a2+b2+c2=6,∴(2a+b+c)2≤36, (7分)! 则 2a+b+c≤6;∵不等式 |x+3|≥2a+b+c对所 有实数 a,b,c都成立, ∴|x+3|≥6,∴x+3≥6或 x+3≤ -6, 则 x≥3或 x≤ -9, 故实数 x的取值范围是:(-∞,-9]∪[3,+∞). (10分)!!!!!!!!!!!!!!!!查看更多