广东高考文科数学试题及答案word精校版
2008年普通高等学校统一考试(广东卷)数学(文科)
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、第二十九届夏季奥林匹克运动会将于2008年8月8日在北京举行,若集合A={参加北京奥运会比赛的运动员},集合B={参加北京奥运会比赛的男运动员},集合C={参加北京奥运会比赛的女运动员},则下列关系正确的是( )
A. B. C. B∪C = A D. A∩B = C
2、已知0
-1 C. a < -1/e D. a > -1/e
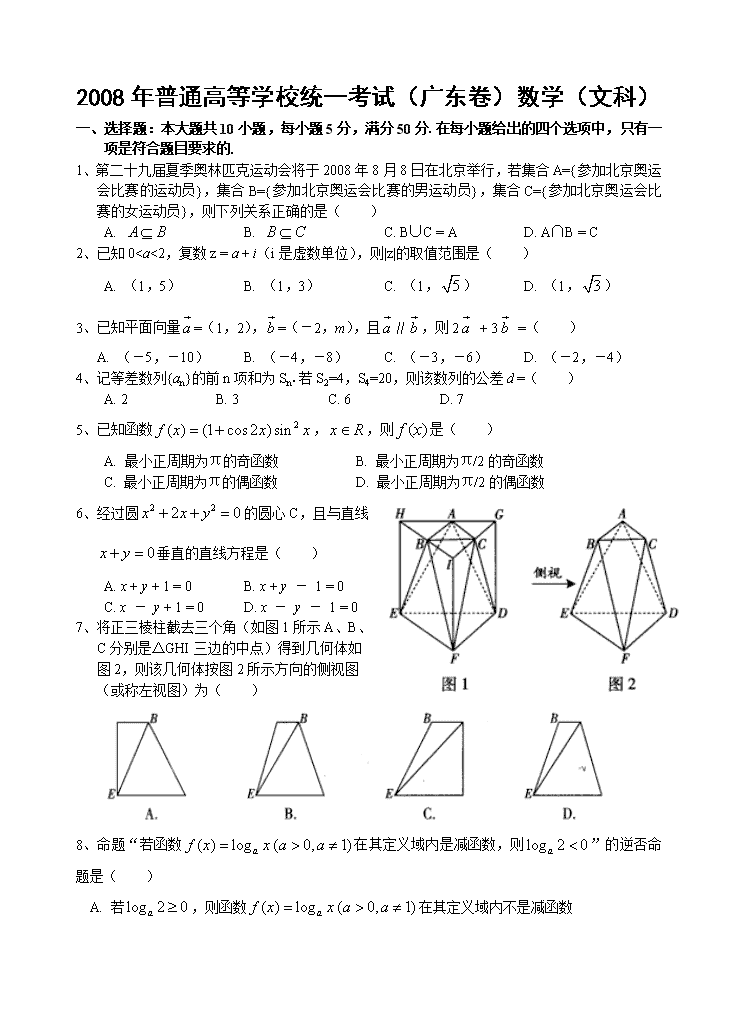
10、设a、b∈R,若a - |b| > 0,则下列不等式中正确的是( )
A. b - a > 0 B. a3 + b3 < 0 C. a2 - b2 < 0 D. b + a > 0
二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
(一)必做题(11~13题)
11、为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量。产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95),由此得到频率分布直方图如图3,则这20名工人中一天生产该产品数量在[55,75)的人数是_______。
12、若变量x、y满足,则的最大值是_______。
13、阅读右上的程序框图。若输入m = 4,n = 3,则输出a = ____,i =_____ 。(注:框图中的赋值符号“=”也可以写成“←”或“:=”)
(二)选做题(14~15题,考生只能从中选做一题)
14、(坐标系与参数方程)已知曲线C1、C2的极坐标方程分别为,(,),则曲线C1与C2交点的极坐标为________
15、(几何证明选讲)已知PA是圆O的切线,切点为A,PA=2。AC是圆O的直径,PC与圆O交于点B,PB=1,则圆O的半径R = ________
三、解答题:本大题共6小题,满分80分。解答须写出文字说明,证明过程和演算步骤。
16、(本小题满分13分)已知函数,的最大值是1,其图像经过点M(π/3,1/2)。(1)求的解析式;(2)已知、,且,,求的值。
17、(本小题满分12分)某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房。经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560 + 48x(单位:元)。为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用 = 平均建筑费用 + 平均购地费用,平均购地费用 = 购地总费用/建筑总面积)。
18、(本小题满分14分)如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP∽△BAD。
(1)求线段PD的长;
(2)若PC = R,求三棱锥P-ABC的体积。
19、(本小题满分13分)某初级中学共有学生2000名,各年级男、女生人数如下表:
一年级
二年级
三年级
女生
373
x
y
男生
377
370
z
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19。(1)求x的值;(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?(3)已知y≥245,z≥245,求初三年级中女生比男生多的概率。
20、(本小题满分14分)设b>0,椭圆方程为,
抛物线方程为。如图所示,过点F(0,b + 2)
作x轴的平行线,与抛物线在第一象限的交点为G。已知抛
物线在点G的切线经过椭圆的右焦点F1。
(1)求满足条件的椭圆方程和抛物线方程;
(2)设A、B分别是椭圆长轴的左、右端点,试探究在抛物
线上是否存在点P,使得△ABP为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标)。
21、(本小题满分14分)设数列满足,,(n = 3,4,…)。数列满足, (n = 2,3,…)是非零整数,且对任意的正整数m和自然数k,都有-1≤…≤1。
(1)求数列和的通项公式;
(2)记(n = 1,2,…),求数列的前n项和。
2008年普通高考广东卷数学(文科)(B卷)参考答案
一、选择题:CCBBD CAAAD
二、填空题:11. 13 12. 70 13. 12 3
14. , 15. ;
三、解答题:
16解:(1)依题意知 A=1
, 又 即
因此 ;
(2) ,且
,
;
17解:设楼房每平方米的平均综合费用为f(x)元,则
令 得
当 时, ;当 时,
因此 当时,f(x)取最小值;
答:为了楼房每平方米的平均综合费最少,该楼房应建为15层。
18解:(1) BD是圆的直径
又 ,
, ;
(2 ) 在中,
又
底面ABCD
三棱锥的体积为 .
19解:(1)
(2)初三年级人数为y+z=2000-(373+377+380+370)=500,
现用分层抽样的方法在全校抽取48名学生,应在初三年级抽取的人数为:
名
(3)设初三年级女生比男生多的事件为A ,初三年级女生男生数记为(y,z);
由(2)知 ,且 ,
基本事件空间包含的基本事件有:
(245,255)、(246,254)、(247,253)、……(255,245)共11个
事件A包含的基本事件有:(251,249)、(252,248)、(253,247)、(254,246)、(255,245) 共5个
;
20解:(1)由得
当时,,G点的坐标为(4,b+2)
,
过点G的切线方程为,即,
令y=0得 ,点的坐标为 (2-b,0);
由椭圆方程得点的坐标为(b,0), 即 b=1,
因此所求的椭圆方程及抛物线方程分别为和。
(2)过A作x轴的垂线与抛物线只有一个交点P,
以为直角的只有一个;
同理以为直角的只有一个;
若以为直角, 设P点的坐标为,则A、B坐标分别为、
由得,
关于的一元二次方程有一解,x有二解,即以为直角的有二个;
因此抛物线上共存在4个点使为直角三角形。
21解:(1)由得
又 ,
数列是首项为1公比为的等比数列,
,
由 得 ,由 得 ,…
同理可得当n为偶数时,;当n为奇数时,;
当n为偶数时
当n为奇数时
因此
当n为偶数时
当n为奇数时
(2)
当n为奇数时,
当n为偶数时,
令 ……①
①×得: ……②
①-②得:
当n为偶数时
当n为奇数时
因此