2021届高考数学一轮总复习课时作业52椭圆及其几何性质含解析苏教版

2021届高考数学一轮总复习课时作业52椭圆及其几何性质含解析苏教版

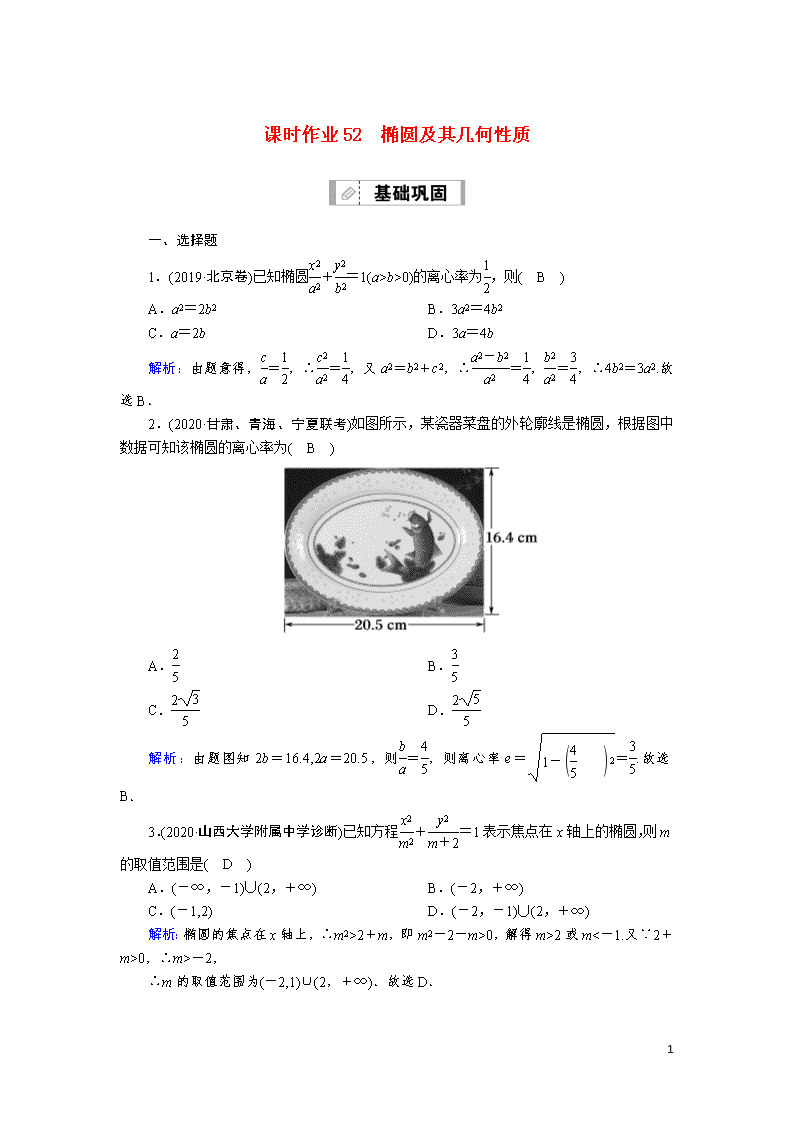
课时作业52　椭圆及其几何性质 一、选择题 ‎1．(2019·北京卷)已知椭圆＋＝1(a>b>0)的离心率为，则(　B　)‎ A．a2＝2b2 B．‎3a2＝4b2‎ C．a＝2b D．‎3a＝4b 解析：由题意得，＝，∴＝，又a2＝b2＋c2，∴＝，＝，∴4b2＝‎3a2.故选B．‎ ‎2．(2020·甘肃、青海、宁夏联考)如图所示，某瓷器菜盘的外轮廓线是椭圆，根据图中数据可知该椭圆的离心率为(　B　)‎ A． B． C． D． 解析：由题图知2b＝16.4,‎2a＝20.5，则＝，则离心率e＝＝.故选B．‎ ‎3．(2020·山西大学附属中学诊断)已知方程＋＝1表示焦点在x轴上的椭圆，则m的取值范围是(　D　)‎ A．(－∞，－1)∪(2，＋∞) B．(－2，＋∞)‎ C．(－1,2) D．(－2，－1)∪(2，＋∞)‎ 解析：椭圆的焦点在x轴上，∴m2>2＋m，即m2－2－m>0，解得m>2或m<－1.又∵2＋m>0，∴m>－2，‎ ‎∴m的取值范围为(－2,1)∪(2，＋∞)．故选D．‎ ‎4．(2020·河北衡水中学摸底)已知椭圆C：＋＝1(a>b>0)和直线l：＋＝1，若过椭圆C的左焦点和下顶点的直线与l平行，则椭圆C的离心率为(　A　)‎ 7‎ A． B． C． D． 解析：因为直线l的斜率为－，且过椭圆C的左焦点和下顶点的直线与直线l平行，所以＝.又b2＋c2＝a2，即2＋c2＝a2，即c2＝a2，所以离心率e＝＝.故选A．‎ ‎5．(2020·福建三明模拟)已知P是椭圆＋＝1上一点，F1，F2分别为椭圆的左、右焦点，且∠F1PF2＝60°，则△F1PF2面积为(　A　)‎ A．3 B．2 C． D． 解析：方法1：由椭圆的标准方程可得a＝5，b＝3，∴c＝4.设|PF1|＝t1，|PF2|＝t2，由椭圆的定义可得t1＋t2＝10①.‎ ‎∵在△F1PF2中，∠F1PF2＝60°，‎ ‎∴根据余弦定理可得|PF1|2＋|PF2|2－2|PF1||PF2|cos60°＝|F‎1F2|2＝(‎2c)2＝64，整理可得t＋t－t1t2＝64②.　把①两边平方得t＋t＋2t1t2＝100 ③，由③－②得t1t2＝12，∴S△F1PF2＝t1t2·sin∠F1PF2＝3.故选A．‎ 方法2：由于椭圆焦点三角形的面积公式为S＝b2tan，故所求面积为9tan30°＝3.故选A．‎ ‎6．(2020·河南郑州一中质量测评)已知F1，F2分别为椭圆C的两个焦点，P为椭圆上任意一点．若的最大值为3，则椭圆C的离心率为(　B　)‎ A． B． C． D． 解析：∵点P到椭圆C的焦点的最大距离为a＋c，最小距离为a－C．又的最大值为3，∴＝3，∴椭圆C的离心率e＝.故选B．‎ ‎7．(2020·宁夏石嘴山质检)已知椭圆＋＝1(a>b>0)的左焦点为F1(－2,0)，过点F1作倾斜角为30°的直线与圆x2＋y2＝b2相交的弦长为b，则椭圆的标准方程为(　A　)‎ A．＋＝1 B．＋＝1‎ C．＋＝1 D．＋＝1‎ 解析：由左焦点为F1(－2,0)，可得a2－b2＝4，过点F1作倾斜角为30°的直线的方程为y 7‎ ‎＝(x＋2)，圆心(0,0)到直线的距离d＝＝1.由直线与圆x2＋y2＝b2相交的弦长为b，可得2＝b，解得b＝2，a＝2，则椭圆方程为＋＝1.故选A．‎ ‎8．(2020·滁州模拟)已知椭圆E：＋＝1(a>b>0)的右焦点为F，短轴的一个端点为M，直线l：3x－4y＝0交椭圆E于A，B两点．若|AF|＋|BF|＝4，点M到直线l的距离不小于，则椭圆E的离心率的取值范围是(　A　)‎ A． B． C． D． 解析：根据椭圆的对称性及椭圆的定义可得，‎ ‎|AF|＋|BF|＝‎2a＝4，所以a＝2.设M(0，b)，‎ 因为d＝≥，所以1≤b<2.‎ 又e＝＝＝，所以0|C‎1C2|＝6，‎ 即P在以C1(－3,0)，C2(3,0)为焦点，长轴长为10的椭圆上，所以点P的轨迹方程为＋＝1.‎ ‎11．设F1，F2为椭圆C：＋＝1的两个焦点，M为C上一点且在第一象限．若△MF‎1F2为等腰三角形，则M的坐标为(3，)．‎ 7‎ 解析：根据题意可知c＝＝4.因为△MF‎1F2为等腰三角形，所以易知|F‎1M|＝‎2c＝8，所以|F‎2M|＝‎2a－8＝4.设M(x，y)，‎ 则得 所以M的坐标为(3，)．‎ ‎12．(2020·嘉兴模拟)已知椭圆＋＝1(a>b>c>0，a2＝b2＋c2)的左、右焦点分别为F1，F2，若以F2为圆心，b－c为半径作圆F2，过椭圆上一点P作此圆的切线，切点为T，且|PT|的最小值不小于(a－c)，则椭圆的离心率e的取值范围是.‎ 解析：因为|PT|＝，|PF2|的最小值为a－c，所以|PT|的最小值为.‎ 依题意，有≥(a－c)，所以(a－c)2≥4(b－c)2，所以a－c≥2(b－c)，所以a＋c≥2b，所以(a＋c)2≥4(a2－c2)，所以‎5c2＋‎2ac－‎3a2≥0，所以5e2＋2e－3≥0.①‎ 又b>c，所以b2>c2，所以a2－c2>c2，所以2e2<1.②‎ 联立①②，得≤e<.‎ 三、解答题 ‎13．(2020·西安模拟)已知椭圆＋＝1(a>b>0)的右焦点为F2(3,0)，离心率为e.‎ ‎(1)若e＝，求椭圆的方程；‎ ‎(2)设直线y＝kx与椭圆相交于A，B两点，M，N分别为线段AF2，BF2的中点，若坐标原点O在以MN为直径的圆上，且b>0)的两个焦点，P为C上的点，O为坐标原点．‎ ‎(1)若△POF2为等边三角形，求C的离心率；‎ ‎(2)如果存在点P，使得PF1⊥PF2，且△F1PF2的面积等于16，求b的值和a的取值范围．‎ 解：(1)连接PF1，由△POF2为等边三角形可知在△F1PF2中，∠F1PF2＝90°，|PF2|＝c，|PF1|＝c，于是‎2a＝|PF1|＋|PF2|＝(＋1)c，故C的离心率e＝＝－1.‎ ‎(2)由题意可知，满足条件的点P(x，y)存在当且仅当 |y|·‎2c＝16，·＝－1，＋＝1，‎ 即c|y|＝16，①‎ x2＋y2＝c2，②‎ ＋＝1.③‎ 由②③及a2＝b2＋c2得y2＝，又由①知y2＝，故b＝4.由②③得x2＝(c2－b2)，所以c2≥b2，从而a2＝b2＋c2≥2b2＝32，故a≥4.‎ 当b＝4，a≥4时，存在满足条件的点P.‎ 所以b＝4，a的取值范围为[4，＋∞)．‎ ‎15．如图所示，圆柱形玻璃杯中水的液面呈椭圆形状，则该椭圆的离心率为(　B　)‎ A． B． C． D． 7‎ 解析：设圆柱的底面半径为1，则椭圆的短半轴长为1，长轴长为＝，即长半轴长为，所以半焦距为，故离心率为.‎ ‎16．(2019·浙江卷)已知椭圆＋＝1的左焦点为F，点P在椭圆上且在x轴的上方．若线段PF的中点在以原点O为圆心，|OF|为半径的圆上，则直线PF的斜率是.‎ 解析：如图，取PF的中点M，连接OM，由题意知|OM|＝|OF|＝2，设椭圆的右焦点为F1，连接PF1，在△PFF1中，OM为中位线，所以|PF1|＝4，由椭圆的定义知|PF|＋|PF1|＝6，所以|PF|＝2.因为M为PF的中点，所以|MF|＝1.在等腰三角形OMF中，过O作OH⊥MF于点H，所以|OH|＝＝，所以kPF＝tan∠HFO＝＝.‎ ‎17．已知点A在椭圆＋＝1上，点P满足＝(λ－1)(λ∈R)，且·＝72，则线段OP在x轴上的投影长度的最大值为15.‎ 解析：∵＝(λ－1)，‎ ‎∴＝λ，则O，P，A三点共线，‎ ‎∵·＝72，∴||||＝72.‎ 设OP与x轴夹角为θ，A(x，y)，B为点A在x轴上的投影，‎ 7‎ 则OP在x轴上的投影长度为||cosθ＝＝72×＝72×≤72×＝15，当且仅当|x|＝时等号成立．则线段OP在x轴上的投影长度的最大值为15.‎ 7‎