高中数学全部知识点总结(供参考)
高中数学必修+选修知识点归纳
必修 1 数学知识点
第一章:集合与函数概念
1、 把研究的对象统称为元素,把一些元素组成的总
体叫做集合。集合三要素:确定性、互异性、无
序性。
2、 常见集合:正整数集合: *N 或 N ,整数集合:
Z ,有理数集合: Q ,实数集合: R .
3、 一般地,对于两个集合 A、B,如果集合 A 中任
意一个元素都是集合 B 中的元素,则称集合 A 是
集合 B 的子集。记作 BA .
4、 如果集合 BA ,但存在元素 Bx ,且 Ax ,
则称集合 A 是集合 B 的真子集.记作:A B.
5、把不含任何元素的集合叫做空集.记作: .并规定:
空集合是任何集合的子集.
6、 如果集合 A 中含有 n 个元素,则集合 A 有 n2 个子
集, 2 1n 个真子集.
7、 一般地,由所有属于集合 A 或集合 B 的元素组成
的集合,称为集合 A 与 B 的并集.记作: BA .
8、 一般地,由属于集合 A 且属于集合 B 的所有元素
组成的集合,称为 A 与 B 的交集.记作: BA .
9、全集、补集? { | , }UC A x x U x U 且
专题一:常用逻辑用语
1、命题:可以判断真假的语句叫命题;
逻辑联结词:“或”“且”“非”这些词就叫做逻辑
联结词;
简单命题:不含逻辑联结词的命题;
复合命题:由简单命题与逻辑联结词构成的命题.
常用小写的拉丁字母 p , q , r , s ,……表示命
题.
2、四种命题及其相互关系
四种命题的真假性之间的关系:
⑴、两个命题互为逆否命题,它们有相同的真假性;
⑵、两个命题为互逆命题或互否命题,它们的真假性
没有关系.
3、充分条件、必要条件与充要条件
⑴、一般地,如果已知 p q ,那么就说: p 是 q 的
充分条件, q 是 p 的必要条件;
若 p q ,则 p 是 q 的充分必要条件,简称充要条件.
⑵、充分条件,必要条件与充要条件主要用来区分命
题的条件 p 与结论 q 之间的关系:
4、复合命题
⑴复合命题有三种形式: p 或 q ( p q ); p 且 q
( p q );非 p ( p ).
⑵复合命题的真假判断
“ p 或 q ”形式复合命题的真假判断方法:一真必真;
“ p 且 q ”形式复合命题的真假判断方法:一假必假;
“非 p ”形式复合命题的真假判断方法:真假相对.
5、全称量词与存在量词
⑴全称量词与全称命题
短语“所有的”“任意一个”在逻辑中通常叫做全称
量词,并用符号“ ”表示.含有全称量词的命题,叫
做全称命题.
⑵存在量词与特称命题
短语“存在一个”“至少有一个”在逻辑中通常叫做
存在量词,并用符号“ ”表示.含有存在量词的命题,
叫做特称命题.
⑶全称命题与特称命题的符号表示及否定
①全称命题 p : , ( )x p x ,它的否定 p :
0 0, ( ).x p x 全称命题的否定是特称命题.
②特称命题 p : 0 0, ( ),x p x ,它的否定 p :
, ( ).x p x 特称命题的否定是全称命题.
§1.2.1、函数的概念
1、 设 A、B 是非空的数集,如果按照某种确定的对应
关系 f ,使对于集合 A 中的任意一个数 x ,在集
合 B 中都有惟一确定的数 xf 和它对应,那么就
称 BAf : 为集合 A 到集合 B 的一个函数,记
作: Axxfy , .
2、 一个函数的构成要素为:定义域、对应关系、值
域.如果两个函数的定义域相同,并且对应关系完
全一致,则称这两个函数相等.
§1.3.1、单调性与最大(小)值
1、注意函数单调性的证明方法:
(1)定义法:设 2121 ],,[ xxbaxx 、 那么
],[)(0)()( 21 baxfxfxf 在 上是增函数;
],[)(0)()( 21 baxfxfxf 在 上是减函数.
步骤:取值—作差—变形—定号—判断
格 式 :解 : 设 baxx ,, 21 且 21 xx , 则 :
21 xfxf =…
(2)导数法:设函数 )(xfy 在某个区间内可导,
若 0)( xf ,则 )(xf 为增函数;
若 0)( xf ,则 )(xf 为减函数.
§1.3.2、奇偶性
1、 一般地,如果对于函数 xf 的定义域内任意一个
x ,都有 xfxf ,那么就称函数 xf 为
偶函数.偶函数图象关于 y 轴对称.
2、 一般地,如果对于函数 xf 的定义域内任意一个
x ,都有 xfxf ,那么就称函数 xf 为
奇函数.奇函数图象关于原点对称.
知识链接:函数与导数
1、函数 )(xfy 在点 0x 处的导数的几何意义:
函数 )(xfy 在点 0x 处的导数是曲线 )(xfy 在
))(,( 00 xfxP 处的切线的斜率 )( 0xf ,相应的切线方
程是 ))(( 000 xxxfyy .
2、几种常见函数的导数
① 'C 0 ;② 1')( nn nxx ;
③ xx cos)(sin ' ; ④ xx sin)(cos ' ;
⑤ aaa xx ln)( ' ; ⑥ xx ee ')( ;
⑦
axxa ln
1)(log ' ;⑧
xx 1)(ln '
3、导数的运算法则
(1) ' ' '( )u v u v .
(2) ' ' '( )uv u v uv .
(3)
' '
'
2( ) ( 0)u u v uv vv v
.
4、复合函数求导法则 (理科)
复合函数 ( ( ))y f g x 的导数和函数
( ), ( )y f u u g x 的导数间的关系为 x u xy y u ,
即 y 对 x 的导数等于 y 对u 的导数与u 对 x 的导数的
乘积.
解题步骤:分层—层层求导—作积还原.
5、函数的极值
(1)极值定义:
极值是在 0x 附近所有的点,都有 )(xf < )( 0xf ,
则 )( 0xf 是函数 )(xf 的极大值;
极值是在 0x 附近所有的点,都有 )(xf > )( 0xf ,
则 )( 0xf 是函数 )(xf 的极小值.
(2)判别方法:
①如果在 0x 附近的左侧 )(' xf >0,右侧 )(' xf <0,
那么 )( 0xf 是极大值;
②如果在 0x 附近的左侧 )(' xf <0,右侧 )(' xf >0,
那么 )( 0xf 是极小值.
6、求函数的最值
(1)求 ( )y f x 在 ( , )a b 内的极值(极大或者极小值)
(2)将 ( )y f x 的各极值点与 ( ), ( )f a f b 比较,其中
最大的一个为最大值,最小的一个为极小值。
注:极值是在局部对函数值进行比较(局部性质);
最值是在整体区间上对函数值进行比较(整体性质)。
第二章:基本初等函数(Ⅰ)
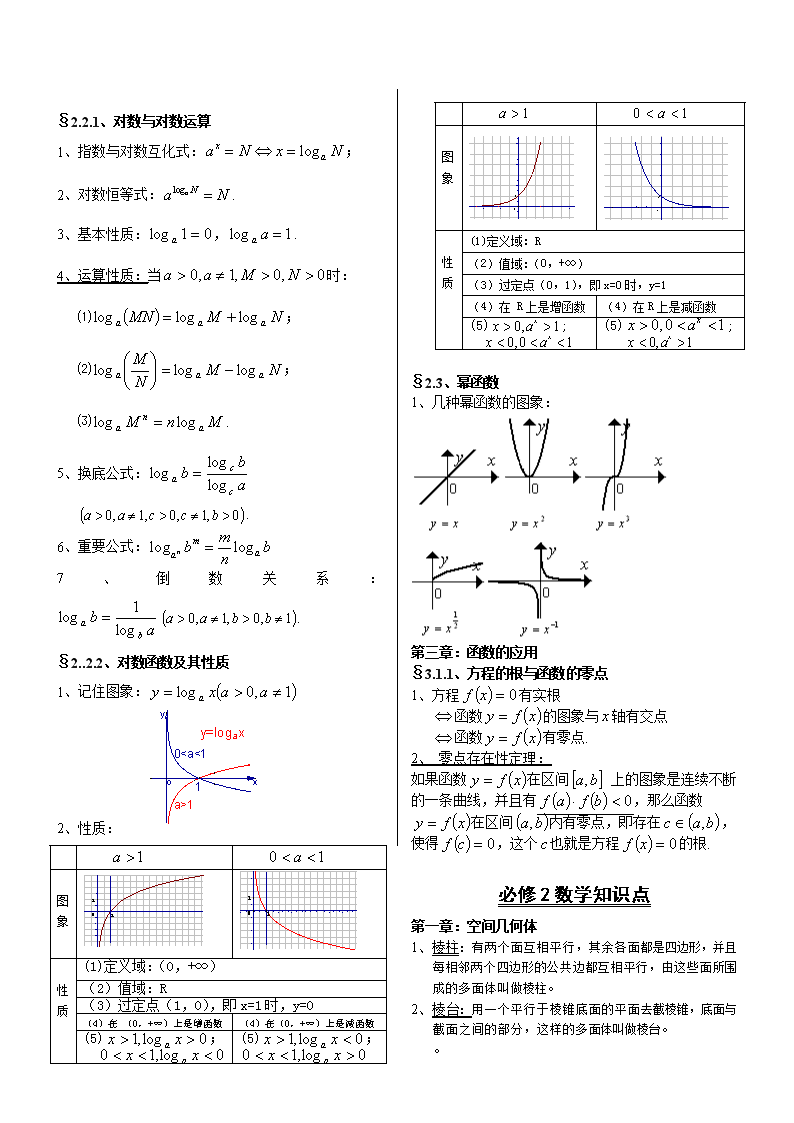
§2.1.2、指数函数及其性质
1、记住图象: 1,0 aaay x
2、性质:
§2.2.1、对数与对数运算
1、指数与对数互化式: logx
aa N x N ;
2、对数恒等式: loga Na N .
3、基本性质: 01log a , 1log aa .
4、运算性质:当 0,0,1,0 NMaa 时:
1a 10 a
图
象
�
6
�
5
�
4
�
3
�
2
�
1
�
-1
�
-4
�
-2
�
2
�
4
�
6
0
1
�
6
�
5
�
4
�
3
�
2
�
1
�
-1
�
-4
�
-2
�
2
�
4
�
6
0
1
性
质
(1)定义域:R
(2)值域:(0,+∞)
(3)过定点(0,1),即 x=0 时,y=1
(4)在 R 上是增函数 (4)在 R 上是减函数
(5) 0, 1xx a ;
0,0 1xx a
(5) 0,0 1xx a ;
0, 1xx a
�
0
1
�
1
�
y=
�
a
�
x
�
o
�
y
�
x
⑴ NMMN aaa logloglog ;
⑵ NMN
M
aaa logloglog
;
⑶ MnM a
n
a loglog .
5、换底公式:
a
bb
c
c
a log
loglog
0,1,0,1,0 bccaa .
6、重要公式: log logn
m
aa
mb bn
7、倒数关系:
ab
b
a log
1log 1,0,1,0 bbaa .
§2..2.2、对数函数及其性质
1、记住图象: 1,0log aaxy a
2、性质:
§2.3、幂函数
1、几种幂函数的图象:
第三章:函数的应用
§3.1.1、方程的根与函数的零点
1、方程 0xf 有实根
函数 xfy 的图象与 x 轴有交点
函数 xfy 有零点.
2、 零点存在性定理:
如果函数 xfy 在区间 ba, 上的图象是连续不断
的一条曲线,并且有 0 bfaf ,那么函数
xfy 在区间 ba, 内有零点,即存在 bac , ,
使得 0cf ,这个 c 也就是方程 0xf 的根.
必修 2 数学知识点
第一章:空间几何体
1、棱柱:有两个面互相平行,其余各面都是四边形,并且
每相邻两个四边形的公共边都互相平行,由这些面所围
成的多面体叫做棱柱。
2、棱台:用一个平行于棱锥底面的平面去截棱锥,底面与
截面之间的部分,这样的多面体叫做棱台。
。
3、空间几何体的表面积与体积
⑴圆柱侧面积; lrS 2侧面
⑵圆锥侧面积: lrS 侧面
⑶圆台侧面积: lRlrS 侧面
⑷体积公式:
hSV 柱体 ; hSV
3
1
锥体 ;
hSSSSV 下下上上台体
3
1
⑸球的表面积和体积:
32
3
44 RVRS 球球 , .
第二章:点、直线、平面之间的位置关系
1、公理 1:如果一条直线上两点在一个平面内,那么这条
直线在此平面内。
2、公理 2:过不在一条直线上的三点,有且只有一个平面。
3、公理 3:如果两个不重合的平面有一个公共点,那么它
1a 10 a
图
象
� 3�
2.5
�
2
�
1.5
�
1
�
0.5
�
-0.5
�
-1
�
-1.5
�
-2
�
-2.5
�
-1
�
1
�
2
�
3
�
4
�
5
�
6
�
7
�
8
0
1
1
� 3�
2.5
�
2
�
1.5
�
1
�
0.5
�
-0.5
�
-1
�
-1.5
�
-2
�
-2.5
�
-1
�
1
�
2
�
3
�
4
�
5
�
6
�
7
�
8
0
1
1
性
质
(1)定义域:(0,+∞)
(2)值域:R
(3)过定点(1,0),即 x=1 时,y=0
(4)在 (0,+∞)上是增函数 (4)在(0,+∞)上是减函数
(5) 0log,1 xx a ;
0log,10 xx a
(5) 0log,1 xx a ;
0log,10 xx a
�
01
�
1
� y=lo� g�
a� x�
o
�
y
�
x
们有且只有一条过该点的公共直线。
4、公理 4:平行于同一条直线的两条直线平行.
5、定理:空间中如果两个角的两边分别对应平行,那么这
两个角相等或互补。
6、线线位置关系:平行、相交、异面。
7、线面位置关系:直线在平面内、直线和平面平行、直
线和平面相交。
8、面面位置关系:平行、相交。
9、线面平行:
⑴判定:平面外一条直线与此平面内的一条直线平行,则
该直线与此平面平行(简称线线平行,则线面平行)。
⑵性质:一条直线与一个平面平行,则过这条直线的任一
平面与此平面的交线与该直线平行(简称线面平行,则
线线平行)。
10、面面平行:
⑴判定:一个平面内的两条相交直线与另一个平面平行,
则这两个平面平行(简称线面平行,则面面平行)。
⑵性质:如果两个平行平面同时和第三个平面相交,那么
它们的交线平行(简称面面平行,则线线平行)。
11、线面垂直:
⑴定义:如果一条直线垂直于一个平面内的任意一条直线,
那么就说这条直线和这个平面垂直。
⑵判定:一条直线与一个平面内的两条相交直线都垂直,
则该直线与此平面垂直(简称线线垂直,则线面垂直)。
⑶性质:垂直于同一个平面的两条直线平行。
12、面面垂直:
⑴定义:两个平面相交,如果它们所成的二面角是直二面
角,就说这两个平面互相垂直。
⑵判定:一个平面经过另一个平面的一条垂线,则这两个
平面垂直(简称线面垂直,则面面垂直)。
⑶性质:两个平面互相垂直,则一个平面内垂直于交线的
直线垂直于另一个平面。(简称面面垂直,则线面垂直)。
第三章:直线与方程
1、倾斜角与斜率:
12
12tan xx
yyk
2、直线方程:
⑴点斜式: 00 xxkyy
⑵斜截式: bkxy
3)一般式: 0 CByAx
3、对于直线:
222111 :,: bxkylbxkyl 有:
⑴
21
21
21 // bb
kkll ;
⑵ 1l 和 2l 相交 1 2k k ;
⑶ 1l 和 2l 重合
21
21
bb
kk ;
⑷ 12121 kkll .
4、对于直线:
0:
,0:
2222
1111
CyBxAl
CyBxAl 有:
⑴
1221
1221
21 // CBCB
BABAll ;
⑵ 1l 和 2l 相交 1221 BABA ;
⑶ 1l 和 2l 重合
1221
1221
CBCB
BABA ;
⑷ 0212121 BBAAll .
5、两点间距离公式:
2
12
2
1221 yyxxPP
6、点到直线距离公式:
22
00
BA
CByAxd
7、两平行线间的距离公式:
1l : 01 CByAx 与 2l : 02 CByAx 平行,
则
22
21
BA
CCd
第四章:圆与方程
1、圆的方程:
⑴标准方程: 222 rbyax
其中圆心为 ( , )a b ,半径为 r .
⑵一般方程: 022 FEyDxyx .
其中圆心为 ( , )
2 2
D E ,半径为 2 21 4
2
r D E F .
2、直线与圆的位置关系
直线 0 CByAx 与圆 222 )()( rbyax
的位置关系有三种:
0 相离rd ;
0 相切rd ;
0 相交rd .
弦长公式: 222 drl
2 2
1 2 1 21 ( ) 4k x x x x
3、两圆位置关系: 21OOd
⑴外离: rRd ;
⑵外切: rRd ;
⑶相交: rRdrR ;
⑷内切: rRd ;
⑸内含: rRd .
3、空间中两点间距离公式:(理科)
2
12
2
12
2
1221 zzyyxxPP
必修 3 数学知识点
第二章:统计
1、抽样方法:
①简单随机抽样(总体个数较少)
②系统抽样(总体个数较多)
③分层抽样(总体中差异明显)
注意:在 N 个个体的总体中抽取出 n 个个体组成样本,
每个个体被抽到的机会(概率)均为
N
n 。
2、总体分布的估计:
⑴一表二图:
①频率分布表——数据详实
②频率分布直方图——分布直观
③频率分布折线图——便于观察总体分布趋势
注:总体分布的密度曲线与横轴围成的面积为 1。
⑵茎叶图:
①茎叶图适用于数据较少的情况,从中便于看出数据
的分布,以及中位数、众位数等。
②个位数为叶,十位数为茎,右侧数据按照从小到大
书写,相同的数据重复写。
3、总体特征数的估计:
⑴平均数:
n
xxxxx n 321 ;
取值为 nxxx ,,, 21 的频率分别为 nppp ,,, 21 ,则其
平均数为 nn pxpxpx 2211 ;
注意:频率分布表计算平均数要取组中值。
⑵方差与标准差:一组样本数据 nxxx ,,, 21
方差:
2
1
2 )(1
n
i
i xxns ;
标准差:
2
1
)(1
n
i
i xxns
注:方差与标准差越小,说明样本数据越稳定。
平均数反映数据总体水平;方差与标准差反映数据的
稳定水平。
⑶线性回归方程
①变量之间的两类关系:函数关系与相关关系;
②制作散点图,判断线性相关关系
③线性回归方程: abxy
(最小二乘法)
1
22
1
n
i i
i
n
i
i
x y nxy
b
x nx
a y bx
注意:线性回归直线经过定点 ),( yx 。
第三章:概率
1、随机事件及其概率:
⑴事件:试验的每一种可能的结果,用大写英文字母
表示;
⑵必然事件、不可能事件、随机事件的特点;
⑶随机事件 A 的概率: 1)(0,)( APn
mAP .
2、古典概型:
⑴基本事件:一次试验中可能出现的每一个基本结果;
⑵古典概型的特点:
①所有的基本事件只有有限个;
②每个基本事件都是等可能发生。
⑶古典概型概率计算公式:一次试验的等可能基本事
件共有 n 个,事件 A 包含了其中的 m 个基本事件,则
事件 A 发生的概率
n
mAP )( .
3、几何概型:
⑴几何概型的特点:
①所有的基本事件是无限个;
②每个基本事件都是等可能发生。
⑵几何概型概率计算公式: 的测度
的测度
D
dAP )( ;
其中测度根据题目确定,一般为线段、角度、面积、
体积等。
4、互斥事件:
⑴不可能同时发生的两个事件称为互斥事件;
⑵如果事件 nAAA ,,, 21 任意两个都是互斥事件,则称
事件 nAAA ,,, 21 彼此互斥。
⑶如果事件 A,B 互斥,那么事件 A+B 发生的概率,
等于事件 A,B 发生的概率的和,
即: )()()( BPAPBAP
⑷如果事件 nAAA ,,, 21 彼此互斥,则有:
)()()()( 2121 nn APAPAPAAAP
⑸对立事件:两个互斥事件中必有一个要发生,则称
这两个事件为对立事件。
①事件 A 的对立事件记作 A
)(1)(,1)()( APAPAPAP
②对立事件一定是互斥事件,互斥事件未必是对立事
件。
必修 4 数学知识点
第一章:三角函数
§1.1.1、任意角
1、 正角、负角、零角、象限角的概念.
2、 与角 终边相同的角的集合:
Zkk ,2 .
§1.1.2、弧度制
1、 把长度等于半径长的弧所对的圆心角叫做 1 弧度
的角.
2、
r
l .
3、弧长公式: RRnl
180
.
4、扇形面积公式: lRRnS 2
1
360
2
.
§1.2.1、任意角的三角函数
1、 设 是一个任意角,它的终边与单位圆交于点
yxP , ,那么:
x
yxy tan,cos,sin
2、 设点 ,A x y 为角 终边上任意一点,那么:(设
2 2r x y )
sin y
r
,cos x
r
,tan y
x
,cot x
y
3、 sin , cos , tan 在
四个象限的符号和三角函
数线的画法.
正弦线:MP;
余弦线:OM;
正切线:AT
4、 特殊角的三角函数值.
0
6
4
3
2
sin
cos
tan
§1.2.2、同角三角函数的基本关系式
1、 平方关系: 1cossin 22 .
2、 商数关系:
cos
sintan .
§1.3、三角函数的诱导公式
(概括为“奇变偶不变,符号看象限” Zk )
1、 诱导公式一:
.tan2tan
,cos2cos
,sin2sin
k
k
k
(其中: Zk )
2、 诱导公式二:
.tantan
,coscos
,sinsin
3、诱导公式三:
.tantan
,coscos,......sinsin
4、诱导公式四:
.tantan
,coscos,......sinsin
5、诱导公式五:
.sin2cos,........cos2sin
6、诱导公式六:
�
T
�
M
�
A
�
O
�
P
�
x
�
y
sin cos ,........cos sin .2 2
图表归纳:正弦、余弦、正切函数的图像及其性质
xy sin xy cos xy tan
图象
定义域 R R },2|{ Zkkxx
值域 [-1,1] [-1,1] R
最值
max
min
2 , 1
2
2 , 1
2
x k k Z y
x k k Z y
时,
时,
max
min
2 , 1
2 , 1
x k k Z y
x k k Z y
时,
时,
无
周期性 2T 2T T
奇偶性 奇 偶 奇
单调性
Zk
在[2 ,2 ]2 2k k 上单调递增
在 3[2 ,2 ]2 2k k 上单调递减
在[2 ,2 ]k k 上单调递增
在[2 ,2 ]k k 上单调递减
在( , )2 2k k 上单调递增
对称性
Zk
对称轴方程:
2
x k
对称中心 ( ,0)k
对称轴方程: x k
对称中心 ( ,0)
2
k
无对称轴
对称中心 , 0)(
2
k
§1.5、函数 xAy sin 的图象
1、对于函数:
sin 0, 0y A x B A 有:振幅 A,周
期 2T
,初相 ,相位 x ,频率
2
1 Tf .
2、能够讲出函数 xy sin 的图象与
siny A x B 的图象之间的平移伸缩变
换关系.
1 先平移后伸缩:
siny x 平移 | | 个单位 siny x
(左加右减)
横坐标不变 siny A x
纵坐标变为原来的 A 倍
纵坐标不变 siny A x
横坐标变为原来的 1| |
倍
平移 | |B 个单位 siny A x B
(上加下减)
2 先伸缩后平移:
siny x 横坐标不变 siny A x
纵坐标变为原来的 A 倍
纵坐标不变 siny A x
横坐标变为原来的 1| |
倍
平移
个单位 siny A x
(左加右减)
平移 | |B 个单位 siny A x B
(上加下减)
3、三角函数的周期,对称轴和对称中心
函数 sin( )y x ,x∈R 及函数 cos( )y x ,
x∈R(A, , 为常数,且 A≠0)的周期 2
| |T
;函
数 tan( )y x , ,2x k k Z (A,ω, 为
常数,且 A≠0)的周期
| |T
.
对 于 sin( )y A x 和 cos( )y A x 来
说,对称中心与零点相联系,对称轴与最值点联系.
求函数 sin( )y A x 图像的对称轴与对称中心,
只需令 ( )
2
x k k Z 与 ( )x k k Z
解出 x 即可.余弦函数可与正弦函数类比可得.
4、由图像确定三角函数的解析式
利用图像特征: max min
2
y yA , max min
2
y yB .
要根据周期来求, 要用图像的关键点来求.
第三章、三角恒等变换
§3.1.1、两角差的余弦公式
记住 15°的三角函数值:
sin cos tan
12
4
26
4
26 32
§3.1.2、两角和与差的正弦、余弦、正切公式
1、 sincoscossinsin
2、 sincoscossinsin
3、 sinsincoscoscos
4、 sinsincoscoscos
5、 tan tan
1 tan tantan
.
6、 tan tan
1 tan tantan
.
§3.1.3、二倍角的正弦、余弦、正切公式
1、 cossin22sin ,
变形: 1
2sin cos sin 2 .
2、 22 sincos2cos
1cos2 2
2sin21 .
变形如下:
升幂公式:
2
2
1 cos2 2cos
1 cos2 2sin
降幂公式:
2
2
1cos (1 cos2 )2
1sin (1 cos2 )2
3、
2tan1
tan22tan
.
§3.2、简单的三角恒等变换
2、辅助角公式
)sin(cossin 22 xbaxbxay
(一般关注 , ,6 4 3
的情况).
解三角形
1、正弦定理:
RC
c
B
b
A
a 2sinsinsin
.
(其中 R 为 ABC 外接圆的半径)
2 sin , 2 sin , 2 sin ;a R A b R B c R C
sin ,sin ,sin ;2 2 2
a b cA B CR R R
: : sin :sin :sin .a b c A B C
用途:⑴已知三角形两角和任一边,求其它元素;
⑵已知三角形两边和其中一边的对角,求其它
元素。
2、余弦定理:
2 2 2
2 2 2
2 2 2
2 cos ,
2 cos ,
2 cos .
a b c bc A
b a c ac B
c a b ab C
2 2 2
2 2 2
2 2 2
cos ,2
cos ,2
cos .2
b c aA bc
a c bB ac
a b cC ab
用途:⑴已知三角形两边及其夹角,求其它元素;
⑵已知三角形三边,求其它元素。
做题中两个定理经常结合使用.
3、三角形面积公式:
BacAbcCabS ABC sin2
1sin2
1sin2
1
4、三角形内角和定理:
在△ABC 中,有 ( )A B C C A B
2 2 2
C A B 2 2 2( )C A B .
5、一个常用结论:
在 ABC 中, sin sin ;a b A B A B
若sin 2 sin 2 , .2A B A B A B 则 或 特别注意,
在三角函数中,sin sinA B A B 不成立。
:平面向量
2、 既有大小又有方向的量叫做向量.
§2.1.2、向量的几何表示
1、 带有方向的线段叫做有向线段,有向线段包含三
个要素:起点、方向、长度.
2、 向量 AB 的大小,也就是向量 AB 的长度(或称
模),记作 AB
;长度为零的向量叫做零向量;长
度等于 1 个单位的向量叫做单位向量.
3、 方向相同或相反的非零向量叫做平行向量(或共
线向量).规定:零向量与任意向量平行.
§2.1.3、相等向量与共线向量
1、 长度相等且方向相同的向量叫做相等向量.
§2.2.1、向量加法运算及其几何意义
1、 三角形加法法则和平行四边形加法法则.
2、 ba ≤ ba .
§2.2.2、向量减法运算及其几何意义
1、 与 a 长度相等方向相反的向量叫做 a 的相反向量.
2、 三角形减法法则和平行四边形减法法则.
§2.2.3、向量数乘运算及其几何意义
2、 平面向量共线定理:向量 0aa 与b 共线,
当且仅当有唯一一个实数 ,使 ab .
§2.3.2、平面向量的正交分解及坐标表示
1、 yxjyixa , .
§2.3.3、平面向量的坐标运算
1、 设 2211 ,,, yxbyxa ,则:
⑴ 2121 , yyxxba ,
⑵ 2121 , yyxxba ,
⑶ 11, yxa ,
⑷ 1221// yxyxba .
2、 设 2211 ,,, yxByxA ,则:
1212 , yyxxAB .
§2.3.4、平面向量共线的坐标表示
1、设 332211 ,,,,, yxCyxByxA ,则
⑴线段 AB 中点坐标为 22
2121 , yyxx ,
⑵△ABC 的重心坐标为 33
321321 , yyyxxx .
§2.4.1、平面向量数量积的物理背景及其含义
1、 cosbaba .
2、 a 在b 方向上的投影为: cosa .
3、
22
aa .
4、 2
aa .
5、 0 baba .
§2.4.2、平面向量数量积的坐标表示、模、夹角
1、 设 2211 ,,, yxbyxa ,则:
⑴ 2121 yyxxba
⑵ 2
1
2
1 yxa
⑶ 1 2 1 20 0a b a b x x y y
⑷ 1 2 2 1/ / 0a b a b x y x y
2、 设 2211 ,,, yxByxA ,则:
2
12
2
12 yyxxAB .
3、 两向量的夹角公式
1 2 1 2
2 2 2 2
1 1 2 2
cos x x y ya b
a b x y x y
必修 5 数学知识点
第二章:数列
1、数列中 na 与 nS 之间的关系:
1
1
, ( 1)
,( 2).n
n n
S na S S n
注意通项能否合并。
2、等差数列:
⑴定义:如果一个数列从第 2 项起,每一项与它的前
一项的差等于同一个常数,即 na - 1na =d ,(n≥
2,n∈N ),
那么这个数列就叫做等差数列。
⑵等差中项:若三数 a A b、 、 成等差数列
2
a bA
⑶通项公式: 1 ( 1) ( )n ma a n d a n m d
或 (na pn q p q 、 是常数).
⑷前 n 项和公式:
1
1
1
2 2
n
n
n n n a aS na d
⑸常用性质:
①若 Nqpnmqpnm ,,, ,则
qpnm aaaa ;
②数列{ na }为等差数列 na pn q (p,q 是常数)
3、等比数列
⑴定义:如果一个数列从第 2 项起,每一项与它的前
一项的比等于同一个常数,那么这个数列就叫做等
比数列。
⑵等比中项:若三数 a b、G、 成等比数列 2 ,G ab
( ab 同号)。反之不一定成立。
⑶通项公式: 1
1
n n m
n ma a q a q
⑷前 n 项和公式: 1 11
1 1
n
n
n
a q a a qS q q
⑸常用性质
①若 Nqpnmqpnm ,,, ,则
m n p qa a a a ;
第三章:不等式
§3.1、不等关系与不等式
1、不等式的基本性质
①(对称性) a b b a
②(传递性) ,a b b c a c
③(可加性) a b a c b c
(同向可加性) dbcadcba ,
(异向可减性) dbcadcba ,
④(可积性) bcaccba 0,
bcaccba 0,
⑤(同向正数可乘性) 0, 0a b c d ac bd
(异向正数可除性) 0,0 a ba b c d c d
⑥(平方法则) 0 ( , 1)n na b a b n N n 且
⑦(开方法则) 0 ( , 1)n na b a b n N n 且
⑧(倒数法则)
babababa 110;110
2、几个重要不等式
① 2 2 2a b ab a b R , ,(当且仅当 a b 时取
" " 号). 变形公式:
2 2
.2
a bab
②(基本不等式)
2
a b ab a b R, ,(当
且仅当 a b 时取到等号).
变形公式: 2a b ab
2
.2
a bab
用基本不等式求最值时(积定和最小,和定积最
大),要注意满足三个条件“一正、二定、三相等”.
绝对值三角不等式 .a b a b a b (理科)
5、一元二次不等式的解法
求一元二次不等式 2 0( 0)ax bx c 或
2( 0, 4 0)a b ac 解集的步骤:
一化:化二次项前的系数为正数.
二判:判断对应方程的根.
三求:求对应方程的根.
四画:画出对应函数的图象.
五解集:根据图象写出不等式的解集.
规律:当二次项系数为正时,小于取中间,大于取两边.
专题五:数系的扩充与复数
1、复数的概念
⑴虚数单位i ;
⑵复数的代数形式 ( , )z a bi a b R ;
⑶复数的实部、虚部,虚数与纯虚数.
2、复数的分类
复数 ,z a bi a b R
( 0)
( 0, 0)( 0) ( 0, 0)
b
a bb a b
实数
纯虚数
虚数
非纯虚数
3、相关公式
⑴ dcbadicbia 且,
⑵ 00 babia
⑶ 22 babiaz
⑷ z a bi
zz, 指两复数实部相同,虚部互为相反数(互为共
轭复数).
4、复数运算
⑴复数加减法: idbcadicbia ;
⑵复数的乘法:
a bi c di ac bd bc ad i ;
⑶复数的除法:
a bi c dia bi
c di c di c di
2 2 2 2 2 2
ac bd bc ad i ac bd bc ad ic d c d c d
(类似于无理数除法的分母有理化 虚数除法的分
母实数化)
5、常见的运算规律
(1) ; (2) 2 , 2 ;z z z z a z z bi
2 2 2 2(3) ;(4) ;(5)z z z z a b z z z z z R
4 1 4 2 4 3 4 4(6) , 1, , 1;n n n ni i i i i i
2
2 1 1 1(7) 1 ;(8) , ,1 1 2
i i ii i i i ii i
)9( 设
2
31 i 是 1 的立方虚根,则
01 2 , 1,, 332313 nnn
6、复数的几何意义
复平面:用来表示复数的直角坐标系,其中 x 轴叫
做复平面的实轴, y 轴叫做复平面的虚轴.
z a bi Z 一一对应复数 复平面内的点(a,b)
z a bi OZ 一一对应复数 平面向量
专题二:圆锥曲线与方程
1.椭圆
焦点的位置 焦点在 x 轴上 焦点在 y 轴上
图形
标准方程
2 2
2 2 1 0x y a ba b
2 2
2 2 1 0y x a ba b
定义 到两定点 21F F、 的距离之和等于常数 2 a ,即 21| | | | 2MF MF a ( 212 | |a F F )
轴长 长轴的长 2a 短轴的长 2b
对称性 关于 x 轴、 y 轴对称,关于原点中心对称
焦点 1 ,0F c 、 2 ,0F c 1 0,F c 、 2 0,F c
焦距 2 2 2
1 2 2 ( )F F c c a b
离心率 (0 1)ce ea
焦点的位置 焦点在 x 轴上 焦点在 y 轴上
图形
标准方程
2 2
2 2 1 0, 0x y a ba b
2 2
2 2 1 0, 0y x a ba b
定义 到两定点 21F F、 的距离之差的绝对值等于常数 2a ,即 21| | | | 2MF MF a ( 210 2 | |a F F )
轴长 实轴的长 2a 虚轴的长 2b
对称性 关于 x 轴、 y 轴对称,关于原点中心对称
焦点 1 ,0F c 、 2 ,0F c 1 0,F c 、 2 0,F c
焦距 2 2 2
1 2 2 ( )F F c c a b
y
y
x
O
M
H
N
双曲线
抛物线:
2、极坐标系的概念
在平面内取一个定点O ,叫做极点;自极点O 引一条射线 Ox 叫做极轴;再选定一个长度单位、一个角度单
位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系。
点 M 的极坐标:设 M 是平面内一点,极点O 与点 M 的距离 || OM 叫做点 M 的极径,记为 ;以极轴Ox
为始边,射线OM 为终边的 xOM 叫做点 M 的极角,记为 。有序数对 ),( 叫做点 M 的极坐标,记为
),( M .
3、极坐标与直角坐标的互化
设 M 是平面内任意一点,它的直角坐标是 ( , )x y ,极坐标是 ( , ) ,从图中可以得出:
2 2 2
cos , sin
, t n ( 0).
x y
yx y a xx
4、简单曲线的极坐标方程
⑴圆的极坐标方程
①以极点为圆心, a 为半径的圆的极坐标方程是 a ;
离心率 ( 1)ce ea
渐近线方程 by xa
ay xb
图形
标准方程
2 2y px
0p
2 2y px
0p
2 2x py
0p
2 2x py
0p
焦点 , 02
pF
, 02
pF 0, 2
pF
0, 2
pF
准线方程
2
px
2
px
2
py
2
py
xO
图 1
M( , )
②以 ( ,0)a )0( a 为圆心, a 为半径的圆的极坐标方程是 cos2a ;
③以 ( , )2a )0( a 为圆心, a 为半径的圆的极坐标方程是 sin2a ;
⑵直线的极坐标方程
①过极点的直线的极坐标方程是 )0( 和 ( 0) . (如图 1)
②过点 )0)(0,( aaA ,且垂直于极轴的直线 l 的极坐标方程是 acos . 化为直角坐标方程为 x a .(如图
2)
③过点 ( , )2A a 且平行于极轴的直线 l 的极坐标方程是 sin a . 化为直角坐标方程为 y a .(如图 4)
6、参数方程的概念
在平面直角坐标系中,如果曲线上任意一点的坐标 yx, 都是某个变数t 的函数
),(
),(
tgy
tfx 并且对于t 的每一
个允许值,由这个方程所确定的点 ),( yxM 都在这条曲线上,那么这个方程就叫做这条曲线的参数方程,联系变
数 yx, 的变数t 叫做参变数,简称参数。
相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程。
7、常见曲线的参数方程
(1)圆 2 2 2( ) ( )x a y b r 的参数方程为 cos
sin
x a r
y b r
( 为参数);
(2)椭圆
2 2
2 2 1( 0)x y a ba b
的参数方程为 cos
sin
x a
y b
( 为参数);
椭圆
2 2
2 2 1( 0)y x a ba b
的参数方程为 cos
sin
x b
y a
( 为参数);
(3)双曲线
2 2
2 2 1( 0)x y a ba b
的参数方程 sec
tan
x a
y b
( 为参数);
双曲线
2 2
2 2 1( 0)y x a ba b
的参数方程 cot
csc
x b
y a
( 为参数);
(4)抛物线 2 2y px 参数方程
22
2
x pt
y pt
(t 为参数, 1
tant );
专题七:随机变量及其分布
1、基本概念
⑴互斥事件:不可能同时发生的两个事件.
如果事件 A B C、 、 ,其中任何两个都是互斥事
件,则说事件 A B C、 、 彼此互斥.
当 A B、 是互斥事件时,那么事件 A B 发生(即
A B、 中有一个发生)的概率,等于事件 A B、 分别发
生的概率的和,即
( ) ( ) ( )P A B P A P B .
⑵对立 事件:其中必有
一个发 生的两个互斥
事件.事 件 A 的对立事
件通常 记着 A .
对立事件的概率和等于 1. ( ) 1 ( )P A P A .
⑶相互独立事件:事件 A(或 B )是否发生对事件 B
(或 A )发生的概率没有影响,(即其中一个事件是
否发生对另一个事件发生的概率没有影响).这样的两
个事件叫做相互独立事件.
当 A B、 是相互独立事件时,那么事件 A B 发生
(即 A B、 同时发生)的概率,等于事件 A B、 分别发
生的概率的积.即
( ) ( ) ( )P A B P A P B .
若 A、B 两事件相互独立,则 A 与 B 、 A 与 B、 A
与 B 也都是相互独立的.
⑷独立重复试验
①一般地,在相同条件下重复做的 n 次试验称为
n 次独立重复试验.
②独立重复试验的概率公式
如果在 1 次试验中某事件发生的概率是 p ,那么
在 n 次独立重复试验中这个试验恰好发生 k 次的概率
( ) (1 ) 0,1 2, .,k k n k
n nP k nk C p p
⑸条件概率:对任意事件 A 和事件 B,在已知事件 A
发生的条件下事件 B 发生的概率,叫做条件概率.记作
P(B|A),读作 A 发生的条件下 B 发生的概率.
公式: ( )( ) , ( ) 0.( )
P ABP B A P AP A
3、离散型随机变量的分布列
⑴概率分布(分布列)
设离散型随机变量 X 可能取的不同值为
1 2,x x ,…, ix ,…, nx ,
X 的每一个值 ix ( 1,2, ,i n )的概率
( )i iP X x p ,则称表
X
1x 2x … ix … nx
P 1p 2p … ip … np
为随机变量 X 的概率分布,简称 X 的分布列.
性质:① 0, 1,2,... ;ip i n ②
1
1.
n
i
i
p
⑵两点分布
如果随机变量 X 的分布列为
则称 X 服从两点分布,并称 ( 1)p P X 为成功概
率.
⑶二项分布
如果在一次试验中某事件发生的概率是 p,那么在
n 次独立重复试验中这个事件恰好发生 k 次的概率是
( ) (1 ) .k k n k
nP X k C p p
其中 0,1,2,..., , 1k n q p ,于是得到随机
变量 X 的概率分布如下:
X 0 1 … k … n
P
0 0 n
nC p q 1 1 1n
nC p q
…
k k n k
nC p q
…
0n n
nC p q
我们称这样的随机变量 X 服从二项分布,记作
pnBX ,~ ,并称 p 为成功概率.
判断一个随机变量是否服从二项分布,关键有三点:
①对立性:即一次试验中事件发生与否二者必居其一;
②重复性:即试验是独立重复地进行了 n 次;
③等概率性:在每次试验中事件发生的概率均相等.
注:⑴二项分布的模型是有放回抽样;
⑵二项分布中的参数是 , , .p k n
⑷超几何分布
一般地, 在含有 M 件次品的 N 件产品中,任取
n 件,其中恰有 X 件次品数,则事件 X k 发生的
概率为 ( ) ( 0,1,2, , )
k n k
M N M
n
N
C CP X k k mC
,于
是得到随机变量 X 的概率分布如下:
X 0 1
P 1 p p
其中 min ,m M n , *, , , ,n N M N n M N N≤ ≤ .
我们称这样的随机变量 X 的分布列为超几何分布列,
且称随机变量 X 服从超几何分布.
注:⑴超几何分布的模型是不放回抽样;
⑵超几何分布中的参数是 , , .M N n 其意义分别是
总体中的个体总数、N 中一类的总数、样本容量.
4、离散型随机变量的均值与方差
⑴离散型随机变量的均值
一般地,若离散型随机变量 X 的分布列为
X
1x 2x … ix … nx
P 1p 2p … ip … np
则称
1 1 2 2 i i n nE X x p x p x p x p 为离散型
随机变量 X 的均值或数学期望(简称期望).它反映了
离散型随机变量取值的平均水平.
性质:① ( ) ( ) .E aX b aE X b
②若 X 服从两点分布,则 ( ) .E X p
③若 pnBX ,~ ,则 ( ) .E X np
⑵离散型随机变量的方差
一般地,若离散型随机变量 X 的分布列为
X
1x 2x … ix … nx
P 1p 2p … ip … np
则称
2
1
( ) ( ( ))
n
i i
i
D X x E X p
为离散型随机变量 X 的
方差,并称其算术平方根 ( )D X 为随机变量 X 的标
准差.它反映了离散型随机变量取值的稳定与波动,集
中与离散的程度.
( )D X 越小, X 的稳定性越高,波动越小,取值
越集中; ( )D X 越大, X 的稳定性越差,波动越大,
取值越分散.
性质:① 2( ) ( ).D aX b a D X
②若 X 服从两点分布,则 ( ) (1 ).D X p P
③若 pnBX ,~ ,则 ( ) (1 ).D X np P
5、正态分布
正态变量概率密度曲线函数表达式:
Rxexf
x
,
2
1 2
2
2
,其中 , 是参数,
且 ,0 .记作 2( , ).N 如下图:
专题三:定积分
2、微积分基本定理(牛顿-莱布尼兹公式)
如果 ( ) ( )F x f x ,且 ( )f x 在 ],[ ba 上可积,则
( ) ( ) ( ) ( )b b
aa
f x dx F x F b F a ,
【 其 中 ( )F x 叫 做 ( )f x 的 一 个 原 函 数 , 因 为
( ) ( ) ( )F x C F x f x 】
4、定积分的性质
⑴ b
a
b
a
dxxfkdxxkf )()( (k 为常数);
⑵ b
a
b
a
b
a
dxxgdxxfdxxgxf )()()()( ;
⑶ ( ) ( ) ( )
b c b
a a c
f x dx f x dx f x dx (其中 )a c b ;
5、定积分的几何意义
X 0 1 … m
P
0 0n
M N M
n
N
C C
C
1 1n
M N M
n
N
C C
C
…
m n m
M N M
n
N
C C
C
定积分 ( )b
a
f x dx 表示在区间[ , ]a b 上的曲线
( )y f x 与直线 x a 、x b 以及 x 轴所围成的平面
图形(曲边梯形)的面积的代数和,即
( )b
a x xf x dx S S 轴上方 轴下方- .(在 x 轴上方的面积取
正号,在 x 轴下方的面积取负号)
6、求曲边梯形面积的方法与步骤
⑴画出草图,在直角坐标系中画出曲线或直线的大致
图像;
⑵借助图形确定出被积函数,求出交点坐标,确定积
分的上、下限;
⑶写出定积分表达式;
⑷求出曲边梯形的面积和,即各积分的绝对值的和.
7、定积分的简单应用
⑴定积分在几何中的应用:
几种常见的曲边梯形面积的计算方法:
(1) x 型区域:
① 由 一 条 曲 线 )其中 0 )()(( xfxfy 与 直 线
)(, babxax 以及 x 轴所围成的曲边梯形的面
积: ( )bS f x dxa= (如图(1));
图(1)
专题六:排列组合与二项式定理
1、基本计数原理
⑴ 分类加法计数原理:(分类相加)
做一件事情,完成它有 n 类办法,在第一类办法中有
1m 种不同的方法,在第二类办法中有 2m 种不同的方
法……在第 n 类办法中有 nm 种不同的方法.那么完成
这件事情共有 nmmmN 21 种不同的方法.
⑵ 分步乘法计数原理:(分步相乘)
做一件事情,完成它需要 n 个步骤,做第一个步骤有
1m 种不同的方法,做第二个步骤有 2m 种不同的方
法……做第 n 个步骤有 nm 种不同的方法.那么完成这
件事情共有 nmmmN 21 种不同的方法.
2、排列与组合
⑴排列定义:一般地,从 n 个不同的元素中任取
nmm 个元素,按照一定的顺序排成一列,叫做从
n 个不同的元素中任取 m 个元素的一个排列.
⑵组合定义:一般地,从 n 个不同的元素中任取
nmm 个元素并成一组,叫做从 n 个不同的元素中
任取 m 个元素的一个组合.
⑶排列数:从 n 个不同的元素中任取 nmm 个元素
的所有排列的个数,叫做从 n 个不同的元素中任取 m
个元素的排列数,记作 m
nA .
⑷组合数:从 n 个不同的元素中任取 nmm 个元素
的所有组合的个数,叫做从 n 个不同的元素中任取 m
个元素的组合数,记作 m
nC .
⑸排列数公式:
① 121 mnnnnAm
n
!mn
nAm
n ! ;
② !nAn
n ,规定 1!0 .
⑹组合数公式:
①
!
121
m
mnnnnC m
n
或
!! mnm
nC m
n ! ;
② mn
n
m
n CC ,规定 10 nC .
⑺排列与组合的区别:排列有顺序,组合无顺序.
⑻排列与组合的联系: m
m
m
n
m
n ACA ,即排列就是先
组合再全排列.
( 1) ( 1) ! ( )( 1) 2 1 ! !
m
m n
n m
m
A n n n m nC m nA m m m n m
⑼排列与组合的两个性质性质
排列 1
1
m
n
m
n
m
n mAAA ;组合 1
1
m
n
m
n
m
n CCC .
⑽解排列组合问题的方法
①特殊元素、特殊位置优先法(元素优先法:先考虑
有限制条件的元素的要求,再考虑其他元素;位置优
先法:先考虑有限制条件的位置的要求,再考虑其他
位置).
②间接法(对有限制条件的问题,先从总体考虑,再
把不符合条件的所有情况去掉).
③相邻问题捆绑法(把相邻的若干个特殊元素“捆绑”
为一个大元素,然后再与其余“普通元素”全排列,
最后再“松绑”,将特殊元素在这些位置上全排列).
④不相邻(相间)问题插空法(某些元素不能相邻或某
些元素要在某特殊位置时可采用插空法,即先安排好
没有限制元条件的元素,然后再把有限制条件的元素
按要求插入排好的元素之间).
⑤有序问题组合法.
⑥选取问题先选后排法.
⑦至多至少问题间接法.
⑧相同元素分组可采用隔板法.
⑨分组问题:要注意区分是平均分组还是非平均分组,
平均分成 n 组问题别忘除以 n!.
3、二项式定理
⑴二项展开公式:
0 1 1 2 2 2n n n n r n r r
n n n na b C a C a b C a b C a b
n n
nC b n N .
⑵二项展开式的通项公式:
NnNrnrbaCT rrnr
nr ,,01 .主要用途
是求指定的项.
⑶项的系数与二项式系数
项的系数与二项式系数是不同的两个概念,但当
二项式的两个项的系数都为 1 时,系数就是二项式系
数.如
在 ( )nax b 的展开式中,第 1r 项的二项式系数
为 r
nC ,第 1r 项的系数为 r n r r
nC a b ;而 1( )nx x
的
展开式中的系数等于二项式系数;二项式系数一定为
正,而项的系数不一定为正.
⑷ nx1 的展开式:
0221101 xCxCxCxCx n
n
n
n
n
n
n
n
n ,
若令 1x ,则有
n
nnnn
nn CCCC 210211 .
二项式奇数项系数的和等于二项式偶数项系数
的和.即 13120 2 n
nnnn CCCC
⑸二项式系数的性质:
(1)对称性:与首末两端“等距离”的两个二项
式系数相等,即 mn
n
m
n CC ;
(2)增减性与最大值:当 1
2
nr 时,二项式系
数C r
n 的值逐渐增大,当 1
2
nr 时,C r
n 的值逐渐减小,
且在中间取得最大值。当 n 为偶数时,中间一项(第
2
n
+1 项)的二项式系数 2
n
nC 取得最大值.当 n 为奇数时,
中间两项(第
2
1n 和
2
1n +1 项)的二项式系数
1 1
2 2
n n
n nC C
相等并同时取最大值.
⑹系数最大项的求法
设第 r 项的系数 rA 最大,由不等式组 1
1
r r
r r
A A
A A
可确定 r .
知识链接:空间向量(理科)
空间向量的许多知识可由平面向量的知识类比而得.
下面对空间向量在立体几何中证明,求值的应用进行
总结归纳.
1、直线的方向向量和平面的法向量
⑴.直线的方向向量:
若 A、B 是直线l 上的任意两点,则 AB
为直线l 的
一个方向向量;与 AB
平行的任意非零向量也是直线l
的方向向量.
⑵.平面的法向量:
若向量 n
所在直线垂直于平面 ,则称这个向量
垂直于平面 ,记作 n ,如果 n ,那么向量 n
叫做平面 的法向量.
⑶.平面的法向量的求法(待定系数法):
①建立适当的坐标系.
②设平面 的法向量为 ( , , )n x y z .
③求出平面内两个不共线向量的坐标
1 2 3 1 2 3( , , ), ( , , )a a a a b b b b .
④根据法向量定义建立方程组 0
0
n a
n b
.
⑤解方程组,取其中一组解,即得平面 的法向量.
(如图)
1、 用向量方法判定空间中的平行关系
⑴线线平行
设直线 1 2,l l 的方向向量分别是 a b
、 ,则要证明 1l ∥
2l ,只需证明 a
∥b
,即 ( )a kb k R
.
即:两直线平行或重合 两直线的方向向量共线。
⑵线面平行
①(法一)设直线l 的方向向量是 a
,平面 的法向
量是u
,则要证明l ∥ ,只需证明 a u ,即 0a u
.
即:直线与平面平行 直线的方向向量与该平面
的法向量垂直且直线在平面外
②(法二)要证明一条直线和一个平面平行,也可
以在平面内找一个向量与已知直线的方向向量是共线
向量即可.
⑶面面平行
若平面 的法向量为u
,平面 的法向量为 v
,要
证 ∥ ,只需证u
∥ v
,即证u v
.
即:两平面平行或重合 两平面的法向量共线。
3、用向量方法判定空间的垂直关系
⑴线线垂直
设直线 1 2,l l 的方向向量分别是 a b
、 ,则要证明
1 2l l ,只需证明 a b ,即 0a b
.
即:两直线垂直 两直线的方向向量垂直。
⑵线面垂直
①(法一)设直线l 的方向向量是 a
,平面 的法向
量是u
,则要证明l ,只需证明 a
∥u
,即 a u
.
②(法二)设直线l 的方向向量是 a
,平面 内的两
个相交向量分别为 m n
、 ,若 0, .
0
a m l
a n
则
即:直线与平面垂直 直线的方向向量与平面的
法向量共线 直线的方向向量与平面内两条不共线
直线的方向向量都垂直。
⑶面面垂直
若平面 的法向量为u
,平面 的法向量为 v
,要
证 ,只需证u v ,即证 0u v
.
即:两平面垂直 两平面的法向量垂直。
4、利用向量求空间角
⑴求异面直线所成的角
已知 ,a b 为两异面直线,A,C 与 B,D 分别是 ,a b
上的任意两点, ,a b 所成的角为 ,
则 cos .
AC BD
AC BD
⑵求直线和平面所成的角
①定义:平面的一条斜线和它在平面上的射影所成
的锐角叫做这条斜线和这个平面所成的角
②求法:设直线l 的方向向量为 a
,平面 的法向量
为u
,直线与平面所成的角为 ,a
与u
的夹角为 ,
则 为 的余角或 的补角
的余角.即有:
coss .in
a u
a u
⑶求二面角
①定义:平面内的一条直线把平面分为两个部分,
其中的每一部分叫做半平面;从一条直线出发的两个
半平面所组成的图形叫做二面角,这条直线叫做二面
角的棱,每个半平面叫做二面角的面
二面角的平面角是指在二面角 l 的棱上
任 取 一 点 O , 分 别 在 两 个 半 平 面 内 作 射 线
lBOlAO , ,则 AOB 为二面角 l 的平
面角.
如图:
②求法:设二面角 l 的两个半平面的法向量
分 别 为 m n
、 , 再 设 m n
、 的 夹 角 为 , 二 面 角
l 的平面角为 ,则二面角 为 m n
、 的夹角
或其补角 .
根据具体图形确定 是锐角或是钝角:
◆如果 是锐角,则 cos cos
m n
m n
,
即 arccos
m n
m n
;
◆ 如果 是钝角,则 cos cos
m n
m n
,
即 arccos
m n
m n
.