【数学】2020届数学(理)一轮复习人教A版第16讲定积分与微积分基本定理作业
课时作业(十六) 第16讲 定积分与微积分基本定理
时间 / 30分钟 分值 / 80分
基础热身
1.[2018·凉山州二诊] 01 (x-ex)dx=( )
A.32-e B.12-e
C.32+e D.12+e
2.汽车以v=(3t+2) m/s的速度做变速直线运动,则从t=1 s至t=2 s经过的路程是( )
A.5 m B.112 m
C.6 m D.132 m
3.-π2π2 (sin x+|sin x|)dx=( )
A.0 B.1
C.2 D.3
4.[2018·成都七中月考] 曲线y=-x2+2x与x轴围成的封闭图形的面积为( )
A.1 B.43
C.3 D.2
5.一物体在力F(x)=4x-1(单位:N)的作用下,沿着与力F(x)相同的方向,从x=1 m处运动到x=3 m处,则力F(x)所做的功为 .
能力提升
6.[2018·北师大附中期中] 若a=12 exdx,b=12 xdx,c=12 1xdx,则a,b,c的大小关系是 ( )
A.a
1),则a的值是( )
A.2 B.3
C.4 D.6
9.[2018·马鞍山质检] 若π4a (sin x+cos x)dx=22,则a的值不可能为( )
A.13π12 B.7π4
C.29π12 D.37π12
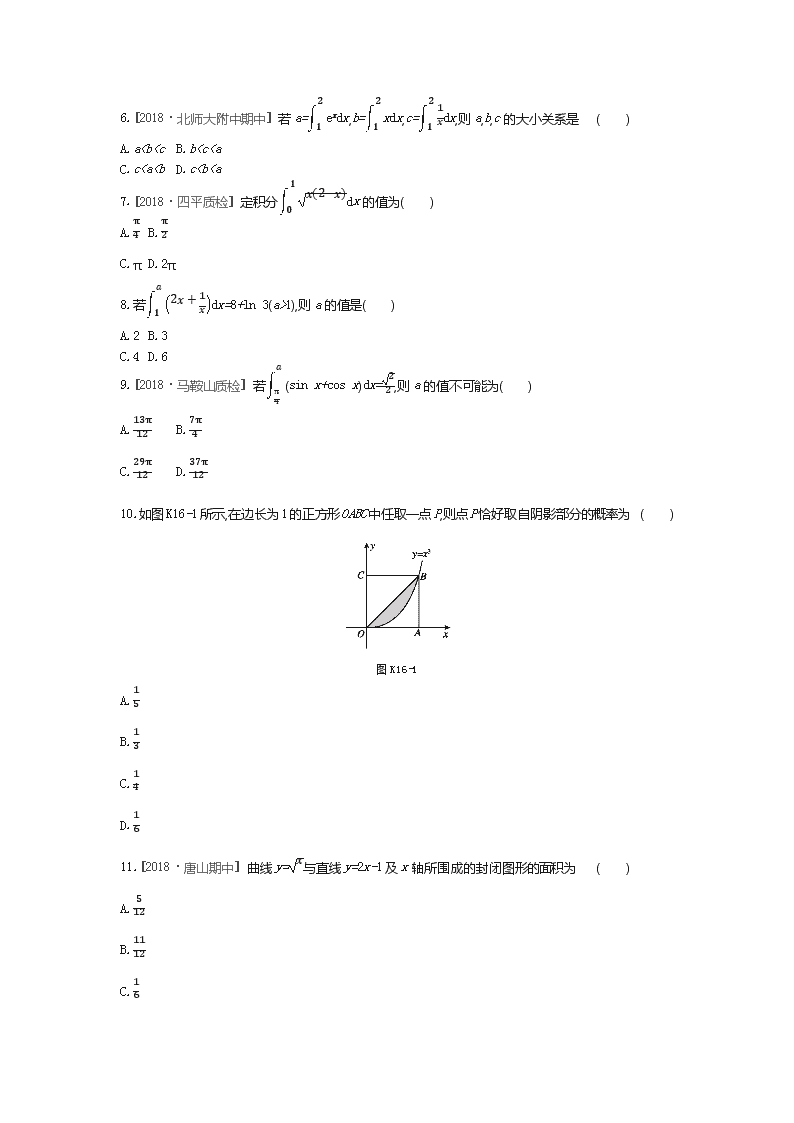
10.如图K16-1所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为 ( )
图K16-1
A.15
B.13
C.14
D.16
11.[2018·唐山期中] 曲线y=x与直线y=2x-1及x轴所围成的封闭图形的面积为 ( )
A.512
B.1112
C.16
D.12
12.[2018·衡水中学模拟] 已知定义在R上的函数f(x)与g(x),若函数f(x)为偶函数,函数g(x)为奇函数,且0a f(x)dx=6,则-aa [f(x)+2g(x)]dx的值为 .
13.[2018·成都三模] 若-11 (ax2+sin x)dx=1,则实数a的值为 .
14.[2018·济宁期末] 直线l过抛物线C:x2=4y的焦点且与y轴垂直,则l与抛物线C所围成的图形的面积为 .
难点突破
15.(5分)[2018·南昌模拟] 如图K16-2所示,在椭圆x24+y2=1内任取一个点P,则P恰好取自椭圆的两个端点连线与椭圆围成的阴影部分的概率为( )
图K16-2
A.14-12π
B.14-14π
C.18
D.18-18π
16.(5分)[2018·三明一模] 考虑函数y=ex与函数y=ln x的图像关系,计算:1e2 ln xdx= .
课时作业(十六)
1.A [解析] 01x-ex)dx=12x2-ex| 01=12-e-(-1)=32-e.
2.D [解析] 所求路程s=123t+2)dt=3t22+2t| 12=6+4-32-2=132(m).
3.C [解析] -π2π2sinx+|sinx|)dx=-π2π2sinxdx+-π2π2sinx|dx=-π2π2sinx|dx=20π2sinxdx=-2cosx| 0π2=2,故选C.
4.B [解析] 易知曲线y=-x2+2x与x轴的交点为(0,0),(2,0),则所求面积S=02x2+2x)dx=-13x3+x2| 02=43.
5.14 J [解析] 力F(x)所做的功W=134x-1)dx=(2x2-x)| 13=14(J).
6.D [解析] ∵a=12exdx=ex| 12=e2-e,b=12xdx=12x2| 12=2-12=32,c=121xdx=lnx| 12=ln2<1,∴c0),
则f'(x)=2x+1x>0,f(x)在(0,+∞)上单调递增,
又f(3)=8+ln 3,所以a=3是方程的唯一解.
9.B [解析] 由题得(-cos x+sin x) π4a=-cos a+sin a--cosπ4+sinπ4=sin a-cos a=2sina-π4=22,
所以sina-π4=12.把a=74π代入上式,得sin7π4-π4=sin3π2=-1,不符合题意,则a的值不可能为7π4,故选B.
10.C [解析] 由题意可知,正方形OABC的面积S=1,阴影部分的面积S0=01x-x3)dx=12x2-14x4| 01=14.则所求概率P=S0S=14.
11.A [解析] 作出曲线y=x及直线y=2x-1,如图所示,则封闭图形如图中阴影部分所示,易知C(1,1),A12,0,过点C向x轴作垂线,垂足为B,则B(1,0),
则所求面积S=01x12dx-12×1-12×1=23-14=512.
12.12 [解析] ∵函数f(x)为偶函数,函数g(x)为奇函数,
∴函数f(x)的图像关于y轴对称,函数g(x)的图像关于原点对称.
∴-aaf(x)dx=20af(x)dx=12,-aag(x)dx=0,∴-aaf(x)+2g(x)]dx=-aaf(x)dx+2-aag(x)dx=12.
13.32 [解析] 因为13ax3'=ax2,(-cos x)'=sin x,
所以-11ax2+sinx)dx=13ax3-cosx| -11=13a-cos1--13a-cos1=23a,所以23a=1,即a=32.
14.83 [解析] 抛物线C:x2=4y的焦点为(0,1),故直线l的方程为y=1.将y=1代入抛物线方程,得x=±2.
所以直线l与抛物线C所围成的图形的面积S=-221-x24dx=x-x312| -22=83.
15.A [解析] 先求椭圆面积的14,由x24+y2=1知y=1-x24,∴S椭圆4=021-x24dx=12024-x2dx,而024-x2dx表示圆x2+y2=4的面积的14,∴024-x2dx=π,∴S椭圆4=12024-x2dx=π2,∴S椭圆=2π,又S阴影=π2-12×2×1=π2-1,
∴所求概率P=π2-12π=14-12π.
16.e2+1 [解析] ∵函数y=ex与函数y=ln x互为反函数,
∴其图像关于直线y=x对称,
作出两函数的图像与边长为e2的正方形OABC,如图所示.记图中两部分阴影区域的面积分别为S1,S2,则由对称性可知S1=S2.易知点E的坐标为(2,e2),则1e2lnxdx=S1=S2=02e2-ex)dx=(e2x-ex)| 02=e2+1.