- 2021-05-19 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2020届一轮复习人教B版(文)第八章38直线、平面垂直的判定与性质作业
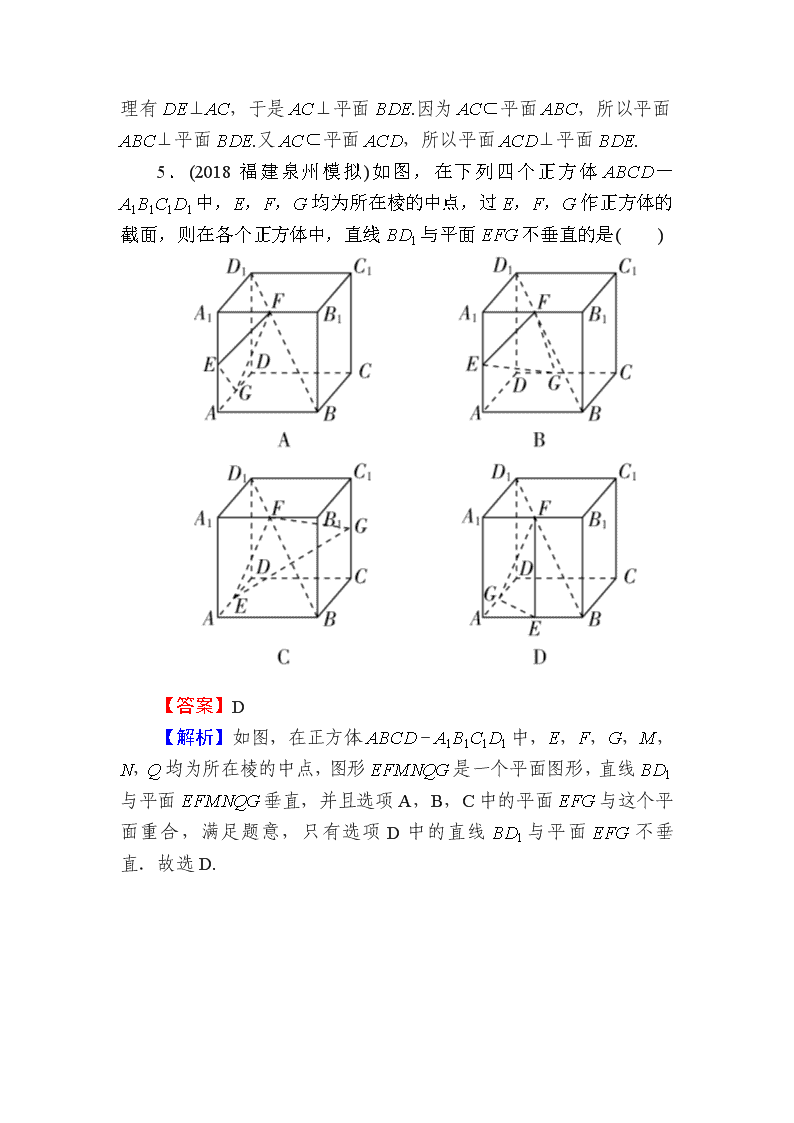
【课时训练】直线、平面垂直的判定与性质 一、选择题 1.(2018天津河西模拟)设l是直线,α,β是两个不同的平面,则下列说法正确的是( ) A.若l∥α,l∥β,则α∥β B.若l∥α,l⊥β,则α⊥β C.若α⊥β,l⊥α,则l∥β D.若α⊥β,l∥α,则l⊥β 【答案】B 【解析】A中,α∥β或α与β相交,不正确. B中,过直线l作平面γ,设α∩γ=l′,则l′∥l,由l⊥β,知l′⊥β,从而α⊥β,B正确. C中,l∥β或l⊂β,C不正确. 对于D中,l与β的位置关系不确定. 2.(2018河南师大附中期末)如图,在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论不成立的是( ) A.BC∥平面PDF B.DF⊥平面PAE C.平面PDF⊥平面PAE D.平面PDE⊥平面ABC 【答案】D 【解析】因为BC∥DF,DF⊂平面PDF,BC⊂平面PDF, 所以BC∥平面PDF,故选项A正确. 在正四面体中,AE⊥BC,PE⊥BC,DF∥BC, 所以BC⊥平面PAE,则DF⊥平面PAE,从而平面PDF⊥平面PAE.因此选项B,C均正确. 3.(2018哈尔滨联考)设m,n是两条不同的直线,α,β是两个不同的平面,则下面结论正确的是( ) A.若m⊥n,n∥α,则m⊥α B.若m∥β,β⊥α,则m⊥α C.若m⊥β,n⊥β,n⊥α,则m⊥α D.若m⊥n,n⊥β,β⊥α,则m⊥α 【答案】C 【解析】A中,由m⊥n,n∥α可得m∥α或m与α相交或m⊥α,错误; B中,由m∥β,β⊥α可得m∥α或m与α相交或m⊂α,错误; C中,由m⊥β,n⊥β可得m∥n,又n⊥α,所以m⊥α,正确; D中,由m⊥n,n⊥β,β⊥α可得m∥α或m与α相交或m⊂α,错误. 4.(2018长沙一模)如图,在三棱锥D-ABC中,若AB=CB,AD=CD,E是AC的中点,则下列命题中正确的是( ) A.平面ABC⊥平面ABD B.平面ABD⊥平面BCD C.平面ABC⊥平面BDE,且平面ACD⊥平面BDE D.平面ABC⊥平面ACD,且平面ACD⊥平面BDE 【答案】C 【解析】因为AB=CB,且E是AC的中点,所以BE⊥AC, 同理有DE⊥AC,于是AC⊥平面BDE.因为AC⊂平面ABC,所以平面ABC⊥平面BDE.又AC⊂平面ACD,所以平面ACD⊥平面BDE. 5.(2018福建泉州模拟)如图,在下列四个正方体ABCD-A1B1C1D1中,E,F,G均为所在棱的中点,过E,F,G作正方体的截面,则在各个正方体中,直线BD1与平面EFG不垂直的是( ) 【答案】D 【解析】如图,在正方体ABCD-A1B1C1D1中,E,F,G,M,N,Q均为所在棱的中点,图形EFMNQG是一个平面图形,直线BD1与平面EFMNQG垂直,并且选项A,B,C中的平面EFG与这个平面重合,满足题意,只有选项D中的直线BD1与平面EFG不垂直.故选D. 6.(2018贵州贵阳二模)如图,在正方形ABCD中,E,F分别是BC,CD的中点,沿AE,AF,EF把正方形折成一个四面体,使B,C,D三点重合,重合后的点记为P,P点在△AEF内的射影为O,则下列说法正确的是( ) A.O是△AEF的垂心 B.O是△AEF的内心 C.O是△AEF的外心 D.O是△AEF的重心 【答案】A 【解析】如图,由题意可知PA,PE,PF两两垂直, 所以PA⊥平面PEF.从而PA⊥EF,而PO⊥平面AEF,则PO⊥EF,因为PO∩PA=P,所以EF⊥平面PAO. 所以EF⊥AO.同理可知AE⊥FO,AF⊥EO, 所以O为△AEF的垂心. 二、填空题 7.(2018吉林九校联考)如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可) 【答案】DM⊥PC(或BM⊥PC等) 【解析】由定理可知BD⊥PC, ∴当DM⊥PC(或BM⊥PC)时,有PC⊥平面MBD. 又PC⊂平面PCD,∴平面MBD⊥平面PCD. 8.(2018云南检测)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=________时,CF⊥平面B1DF. 【答案】A或2a 【解析】∵B1D⊥平面A1ACC1,∴CF⊥B1D. 为了使CF⊥平面B1DF,只要使CF⊥DF(或CF⊥B1F). 设AF=x,则CD2=DF2+FC2, ∴x2-3ax+2a2=0,解得x=a或x=2a. 三、解答题 9.(2018广东七校联考)如图所示,M,N,K分别是正方体ABCD-A1B1C1D1的棱AB,CD,C1D1的中点. 求证:(1)AN∥平面A1MK; (2)平面A1B1C⊥平面A1MK. 【证明】(1)如图所示,连接NK. 在正方体ABCD-A1B1C1D1中, ∵四边形AA1D1D,DD1C1C都为正方形, ∴AA1∥DD1,AA1=DD1,C1D1∥CD,C1D1=CD. ∵N,K分别为CD,C1D1的中点, ∴DN∥D1K,DN=D1K. ∴四边形DD1KN为平行四边形. ∴KN∥DD1,KN=DD1.∴AA1∥KN,AA1=KN. ∴四边形AA1KN为平行四边形.∴AN∥A1K. ∵A1K⊂平面A1MK,AN⊄平面A1MK, ∴AN∥平面A1MK. (2)如图所示,连接BC1.在正方体ABCD-A1B1C1D1中,AB∥C1D1,AB=C1D1. ∵M,K分别为AB,C1D1的中点, ∴BM∥C1K,BM=C1K. ∴四边形BC1KM为平行四边形.∴MK∥BC1. 在正方体ABCD-A1B1C1D1中,A1B1⊥平面BB1C1C, BC1⊂平面BB1C1C,∴A1B1⊥BC1. ∵MK∥BC1,∴A1B1⊥MK. ∵四边形BB1C1C为正方形,∴BC1⊥B1C. ∴MK⊥B1C. ∵A1B1⊂平面A1B1C,B1C⊂平面A1B1C,A1B1∩B1C=B1, ∴MK⊥平面A1B1C. 又∵MK⊂平面A1MK, ∴平面A1B1C⊥平面A1MK. 10.(2018济南模拟)圆O的直径AB=4,点C,D为圆O上两点,且∠CAB=45°,F为的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图②). 图① 图② (1)求证:OF∥平面ACD; (2)在AD上是否存在点E,使得平面OCE⊥平面ACD?若存在,试指出点E的位置;若不存在,请说明理由. 【证明】(1)由∠CAB=45°,知∠COB=90°,又因为F为的中点, 所以∠FOB=45°,因此OF∥AC. 又AC⊂平面ACD,OF⊄平面ACD, 所以OF∥平面ACD. (2)存在,E为AD的中点. 因为OA=OD,所以OE⊥AD. 又OC⊥AB且两半圆所在平面互相垂直, 所以OC⊥平面OAD. 又AD⊂平面OAD,所以AD⊥OC. 由于OE,OC是平面OCE内的两条相交直线,所以AD⊥平面OCE. 又AD⊂平面ACD, 所以平面OCE⊥平面ACD. 11.(2018北京东城区模拟)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC的中点.AB=BC,AC=2,AA1=. (1)求证:B1C∥平面A1BM; (2)求证:AC1⊥平面A1BM; (3)在棱BB1上是否存在点N,使得平面AC1N⊥平面AA1C1C?如果存在,求此时的值;如果不存在,请说明理由. (1)【证明】如图1,连接AB1与A1B,两线交于点O,连接OM, 在△B1AC中,∵M,O分别为AC,AB1中点, 图1 ∴OM∥B1C. 又∵OM⊂平面A1BM,B1C⊄平面A1BM, ∴B1C∥平面A1BM. (2)【证明】∵侧棱AA1⊥底面ABC,BM⊂平面ABC,∴AA1⊥BM. 又∵M为棱AC的中点,AB=BC, ∴BM⊥AC. ∵AA1∩AC=A,∴BM⊥平面ACC1A1. ∴BM⊥AC1. ∵AC=2,∴AM=1. 又∵AA1=,∴在Rt△ACC1和Rt△A1AM中, tan∠AC1C=tan∠A1MA=. ∴∠AC1C=∠A1MA, 即∠AC1C+∠C1AC=∠A1MA+∠C1AC=90°. ∴A1M⊥AC1. ∵BM∩A1M=M,∴AC1⊥平面A1BM. (3)【解】当点N为BB1的中点,即=时,平面AC1N⊥平面AA1C1C. 证明如下:设AC1的中点为D,连接DM,DN,如图2. 图2 ∵D,M分别为AC1,AC的中点, ∴DM∥CC1,且DM=CC1. 又∵N为BB1的中点, ∴DM∥BN,且DM=BN. ∴四边形BNDM为平行四边形. ∴BM∥DN. ∵BM⊥平面ACC1A1,∴DN⊥平面ACC1A1. 又∵DN⊂平面AC1N,∴平面AC1N⊥平面AA1C1C.查看更多