【数学】2018届一轮复习苏教版第64课时直线与平面平行的判定和性质(1)学案

【数学】2018届一轮复习苏教版第64课时直线与平面平行的判定和性质(1)学案

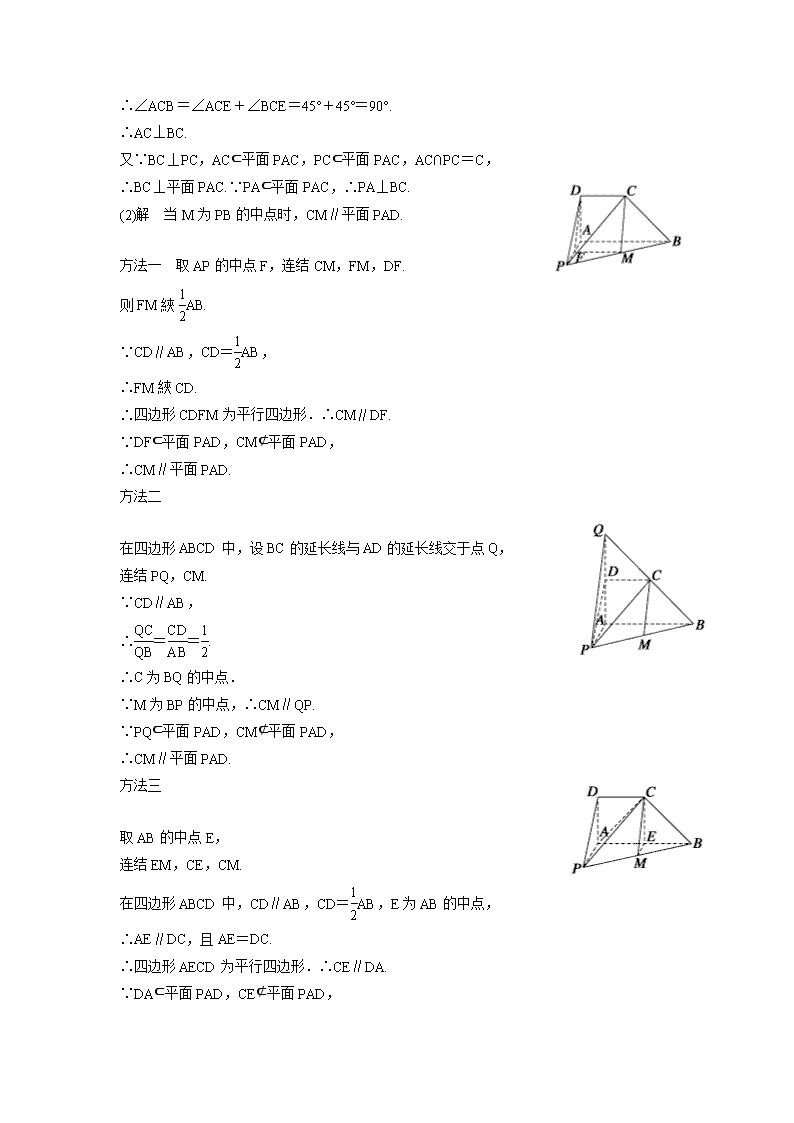
第64课时 线面、面面平行的判定与性质(1)‎ ‎【教学目标】‎ ‎1.了解空间中直线与平面、平面与平面的位置关系及分类标准；‎ ‎2.掌握直线与平面平行、平面与平面平行的判定定理及性质定理，会应用它证明有关的问题；‎ ‎【自主练习 】‎ ‎1．平面a内有不共线的三点到平面b的距离相等，则a与b的关系是 平行或相交 ‎ ‎2.给出以下六个命题：①垂直于同一直线的两个平面平行；②平行于同一直线的两个平面平行；③平行于同一平面的两个平面平行；④与同一直线成等角的两个平面平行；⑤一个平面内的两条相交直线于另一个平面内的两条相交直线平行，则这两个平面平行；⑥两个平面分别与第三个平面相交所得的两条交线平行，则这两个平面平行。其中正确的序号是__① _③__⑤__； ‎ ‎3. 夹在两个平行平面a、b之间的线段AB=8，且AB与a成45º角则a与b之间的距离为 ‎ ‎4. 、表示平面，、表示直线，则的一个充分条件是 ‎ ‎，且 ，且 ‎，且 ，且 ‎5.已知m、n是两条不重合的直线，α，β，γ是三个两两不重合的平面，给出下列命题：‎ ‎①若m∥α，n∥α，m∥β，n∥β，则α∥β；②若α⊥γ，β⊥γ，α∩β＝m，n⊂γ，则m⊥n；‎ ‎③若m⊥α，α⊥β，m∥n，则n∥β；④若n∥α，n∥β，α∩β＝m，那么m∥n.‎ 其中正确命题的序号是__②___④___．‎ ‎6.正方体中,P是面上一点若DP//平面则P的轨迹 ]‎ 是 .‎ ‎【典型例题】‎ A B C D N M A1111‎ B11‎ D11‎ C1111‎ 例1．如图，在正方体ABCD—A1B‎1C1D1中，点N在BD上，点M在B‎1C上，并且CM=DN.‎ 求证:MN∥平面AA1B1B.‎ 证明：连结BM并延长交C‎1C与点F,连结DF 又因为B1B∥C‎1C所以 所以 B‎1C=BD, CM=DN ‎ MN∥DF ‎ 又 MN面DD‎1C1C., DF DD‎1C1C.‎ ‎ MN∥面DD‎1C1C.‎ 又面AA1B1B.∥面DD‎1C1C，MN面AA1B1B.‎ 所以MN∥平面AA1B1B.‎ 例2．如图，已知是平行四边形所在平面外一点，、分别是、的中点求证：平面；‎ M A B C N P D 方法一：取PD中点E，连结NE,AE则NE平行且等于AM.，所以四边形AMNE为平行四边形，所以AD，‎ 又因为MN不在平面PAD内，AE在平面PAD内，所以平面 ‎ ‎ 方法二：取CD中点F连结NF,MF证明面MNF平行于面PAD，从而平面 例3：如图所示，在四棱锥P—ABCD中，CD∥AB，AD⊥AB，AD＝DC＝AB，BC⊥PC.‎ ‎(1)求证：PA⊥BC；‎ ‎(2)试在线段PB上找一点M，使CM∥平面PAD，并说明理由．[来源:Z|xx|k.Com]‎ ‎(1)证明　连结AC，过点C作CE⊥AB，垂足为E.‎ 在四边形ABCD中，AD⊥AB，CD∥AB，AD＝DC，‎ ‎∴四边形ADCE为正方形．‎ ‎∴∠ACD＝∠ACE＝45°.‎ ‎∵AE＝CD＝AB，∴BE＝AE＝CE.∴∠BCE＝45°.‎ ‎∴∠ACB＝∠ACE＋∠BCE＝45°＋45°＝90°.‎ ‎∴AC⊥BC.‎ 又∵BC⊥PC，AC⊂平面PAC，PC⊂平面PAC，AC∩PC＝C，‎ ‎∴BC⊥平面PAC.∵PA⊂平面PAC，∴PA⊥BC.‎ ‎(2)解　当M为PB的中点时，CM∥平面PAD.‎ 方法一　取AP的中点F，连结CM，FM，DF.‎ 则FM綊AB.‎ ‎∵CD∥AB，CD＝AB，‎ ‎∴FM綊CD.‎ ‎∴四边形CDFM为平行四边形．∴CM∥DF.‎ ‎∵DF⊂平面PAD，CM⊄平面PAD，‎ ‎∴CM∥平面PAD.‎ 方法二　‎ 在四边形ABCD中，设BC的延长线与AD的延长线交于点Q，‎ 连结PQ，CM.‎ ‎∵CD∥AB，‎ ‎∴＝＝.‎ ‎∴C为BQ的中点．‎ ‎∵M为BP的中点，∴CM∥QP.‎ ‎∵PQ⊂平面PAD，CM⊄平面PAD，‎ ‎∴CM∥平面PAD.‎ 方法三　‎ 取AB的中点E，‎ 连结EM，CE，CM.‎ 在四边形ABCD中，CD∥AB，CD＝AB，E为AB的中点，‎ ‎∴AE∥DC，且AE＝DC.‎ ‎∴四边形AECD为平行四边形．∴CE∥DA. [来源: ]‎ ‎∵DA⊂平面PAD，CE⊄平面PAD，‎ ‎∴CE∥平面PAD.‎ 同理，根据E，M分别为BA，BP的中点，得EM∥平面PAD.‎ ‎∵CE⊂平面CEM，EM⊂平面CEM，CE∩EM＝E，‎ ‎∴平面CEM∥平面PAD.‎ ‎∵CM⊂平面CEM，∴CM∥平面PAD.‎ 变式：　如图所示，在正方体ABCD—A1B‎1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，问：当点Q在什么位置时，平面D1BQ∥平面PAO?‎ 解　当Q为CC1的中点时，平面D1BQ∥平面PAO. ‎ ‎∵Q为CC1的中点，P为DD1的中点，∴QB∥PA.‎ ‎∵P、O为DD1、DB的中点，∴D1B∥PO.‎ 又PO∩PA＝P，D1B∩QB＝B，D1B∥平面PAO，QB∥平面PAO，∴平面D1BQ∥平面PAO.‎ ‎ ‎