- 2021-05-12 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版初中数学平面直角坐标系(第1课时)教案
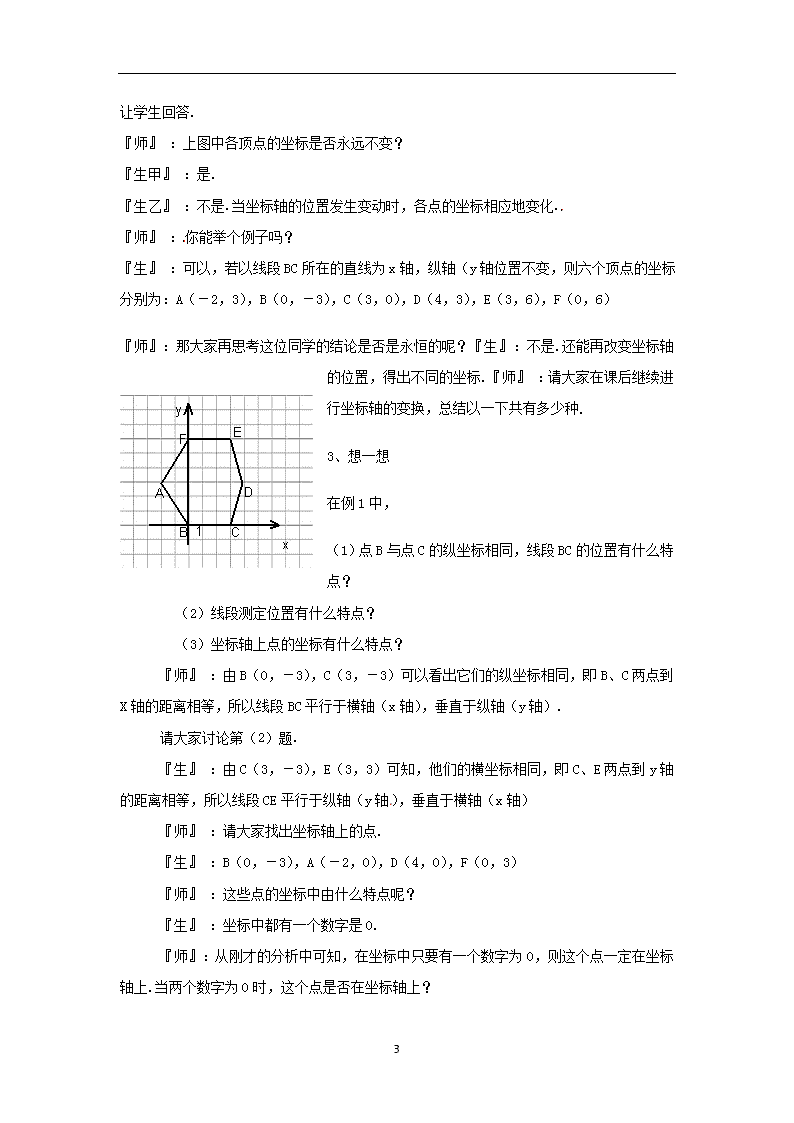
5.2平面直角坐标系(一) 教学目标: 【知识目标】1、理解平面直角坐标系以及横轴、纵轴、原点、坐标等的概念. 2、认识并能画出平面直角坐标系. 3、能在给定的直角坐标系中,由点的位置写出它的坐标. 【能力目标】1、通过画坐标系,由点找坐标等过程,发展学生的数形结合意识,合作交流意识.2、通过对一些点的坐标进行观察,探索坐标轴上点的坐标有什么特点,纵坐标或横坐标相同的点所连成的线段与两坐标轴之间的关系,培养学生的探索意识和能力. 【情感目标】由平面直角坐标系的有关内容,以及由点找坐标,反映平面直角坐标系与现实世界的密切联系,让学生认识数学与人类生活的密切联系和对人类历史发展的作用,提高学生参加数学学习活动的积极性和好奇心. 教学重点: 1、 理解平面直角坐标系的有关知识. 2、在给定的平面直角坐标系中,会根据点的位置写出它的坐标.3、由点的坐标观察,纵坐标或横坐标相同的点所连成的线段与两坐标轴之间的关系,说明坐标轴上点的坐标有什么特点. 教学难点: 1、 横(或纵)坐标相同的点的连线与坐标轴的关系的探究. 2、 坐标轴上点的坐标有什么特点的总结. 教学方法:讨论式学习法 教学过程设计: 一、导入新课 『师』 :同学们,你们喜欢旅游吗? 假如你到了某一个城市旅游,那么你应怎样确定旅游景点的位置呢?下面给出一张某市旅游景点的示意图,根据示意图,回答以下问题:(图5-6) (1) 你是怎样确定各个景点位置的? 5 (1) “大成殿”在“中心广场”南、西各多少个格?“碑林”在“中心广场”北、东各多少个格? (2) 如果以“中心广场”为原点作两条互相垂直的数轴、分别取向右、向上的方向为数轴的正方向,一个方格的边长看做一个单位长度,那么你能表示“碑林”的位置吗?“大成殿”的位置呢? 在上一节课,我们已经学习了许多确定位置的方法,主要学习用反映极坐标思想的定位方式,和用反映直角坐标思想的定位方式.在这个问题中大家看用哪种方法比较合适? 『生』 :用反映直角坐标思想的定位方式. 『师』 :在上一节课中我们已经做过这方面的练习,现在应怎样表示呢?这就是本节课的任务. 二、新课学习 1、 平面直角坐标系、横轴、纵轴、横坐标、纵坐标、原点的定义和象限的划分. 『师』 :看书,倒数第二段P130 ~P131第一段.(三分钟后)请一位同学加以叙述. 『生』 :在平面内,两条互相垂直用公共原点的数轴组成平面直角坐标系.通常,……有序实数对(a,b)叫做点P的坐标. 『师』 :在了解有关直角坐标系的知识后,我们再返回刚才讨论的问题中,请大家思考后回答. 『生』 :(2)“大成殿”在“中心广场”南两格,西两格.“碑林”在“中心广场”北一格,东三格. (3)如果以“中心广场”为原点作两条互相垂直的数轴、分别取向右、向上的方向为数轴的正方向,一个方格的边长看做一个单位长度,则 “碑林”的位置是(3,1).“大成殿”的位置是(-2,-2). 『师』 :很好,在(3)的条件下,你能把其他景点的位置表示出来吗? 『生』 :能,钟楼的位置是(-2,1),雁塔的位置是(0,3),影月湖的位置是(0,-5),科技大学的位置是(-5,-7). 2、 例题讲解 (出示投影)例1 书P131 例1 写出图中的多边形ABCDEF各各顶点的坐标. 5 让学生回答. 『师』 :上图中各顶点的坐标是否永远不变? 『生甲』 :是. 『生乙』 :不是.当坐标轴的位置发生变动时,各点的坐标相应地变化. 『师』 :你能举个例子吗? 『生』 :可以,若以线段BC所在的直线为x轴,纵轴(y轴位置不变,则六个顶点的坐标分别为:A(-2,3),B(0,-3),C(3,0),D(4,3),E(3,6),F(0,6) 『师』 :那大家再思考这位同学的结论是否是永恒的呢?『生』 :不是.还能再改变坐标轴的位置,得出不同的坐标.『师』 :请大家在课后继续进行坐标轴的变换,总结以一下共有多少种. 3、想一想 在例1中, (1)点B与点C的纵坐标相同,线段BC的位置有什么特点? (2)线段测定位置有什么特点? (3)坐标轴上点的坐标有什么特点? 『师』 :由B(0,-3),C(3,-3)可以看出它们的纵坐标相同,即B、C两点到X轴的距离相等,所以线段BC平行于横轴(x轴),垂直于纵轴(y轴). 请大家讨论第(2)题. 『生』 :由C(3,-3),E(3,3)可知,他们的横坐标相同,即C、E两点到y轴的距离相等,所以线段CE平行于纵轴(y轴),垂直于横轴(x轴) 『师』 :请大家找出坐标轴上的点. 『生』 :B(0,-3),A(-2,0),D(4,0),F(0,3) 『师』 :这些点的坐标中由什么特点呢? 『生』 :坐标中都有一个数字是0. 『师』 :从刚才的分析中可知,在坐标中只要有一个数字为0,则这个点一定在坐标轴上.当两个数字为0时,这个点是否在坐标轴上? 5 『生』 :当两个数字都为0时,就是坐标原点(0,0),原点既在x轴上,又在y轴上. 『师』 :那如何确定在哪个坐标轴上呢? 『生 』 :A(-2,0),D(4,0)在x轴上,可以看出这两个点的纵坐标为0,横坐标不为0;B(0,-3),F(0,3)在y轴上,可知它们的横坐标为0,纵坐标不为0. 『师』 :经过大家的共同探讨,我们可以总结出:坐标轴上的点的坐标中至少又一个是0;横轴上的点的纵坐标为0,纵轴上的点的横坐标为0. 『师』 :刚才已知x轴、y轴把坐标平面分成四个象限,但是坐标轴上的点不属于任何一个象限. 各个象限内的点的坐标特征是怎样的? 『生』 :第一象限(+,+), 第二象限(-,+), 第三象限(-,-), 第四象限(+,-). 4、做一做 (出示投影) 书P131 『师』 :请大家先独立思考,然后再进行交流. 『生』 :A(-3,4),B(-6,-2),C(6,-2),D(9,4) A与D两点的纵坐标,B与C两点的纵坐标相同,因为AD、BC分别平行于横轴,A与B,C与D的横坐标不同,因为AB与CD是与x轴斜交,他们向横轴作垂线,垂足不同. 三、随堂练习 补充:1、在下图中,确定A、B、C、D、E、F、G的坐标. 5 (第1题) (第2题) 2、如右图,求出A、B、C、D、E、F的坐标. 四、本课小结 1、 认识并能画出平面直角坐标系. 2、 在给定的直角坐标系中,由点的位置写出它的坐标. 3、 能适当建立直角坐标系,写出直角坐标系中有关点的坐标. 4、 横(纵)坐标相同的点的直线平行于y轴,垂直于x轴;连接纵坐标相同的点的直线平行于x轴,垂直于y轴. 5、 坐标轴上点的纵坐标为0;纵坐标轴上点的坐标为0. 6、各个象限内的点的坐标特征是:第一象限(+,+), 第二象限(-,+), 第三象限(-,-), 第四象限(+,-). 五、课后作业 5查看更多