七年级上册数学课件《实际问题与一元一次方程》 人教新课标 (5)

七年级上册数学课件《实际问题与一元一次方程》 人教新课标 (5)

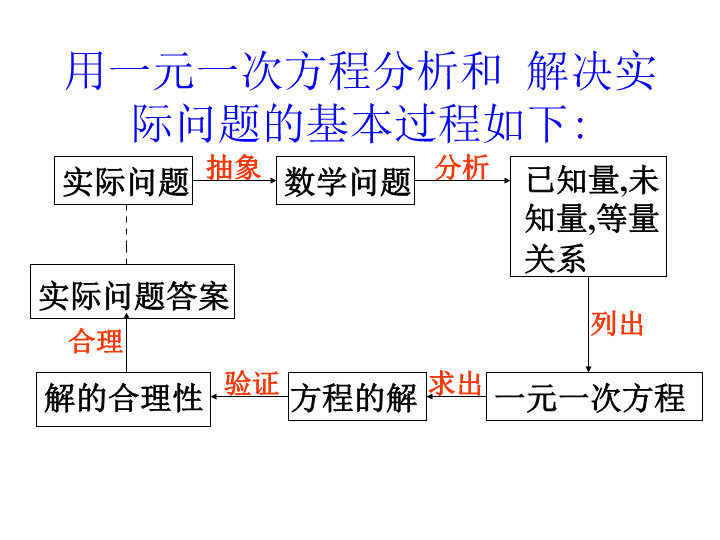
等积变形问题 运用方程解决实际问题的一般过程是什么？ 1、审题：分析题意，找出题中的数量及 其关系； 2、设元：选择一个适当的未知数用字母表 示（例如x）； 3、列方程：根据相等关系列出方程； 4、解方程：求出未知数的值； 5、检验：检查求得的值是否正确和符合 实际情形，并写出答案。 审 设 列 解 验 用一元一次方程分析和 解决实 际问题的基本过程如下: 实际问题 数学问题 已知量,未 知量,等量 关系 一元一次方程方程的解解的合理性 实际问题答案 抽象 分析 列出 求出验证 合理 • 例1、一标志性建筑的 底面是正方形，在其 四周铺上花岗石，形 成一个宽为3米的正方 形边框，已知铺上这 个边框恰好用了192块 边长为0.75米的正方形 花岗石，问标志性建 筑的底面边长是多少 米？ 3 X 分析：若用x表示标志性建筑的底 面边长，本题的等量关系是什么？ 阴影部分的面积＝ 192块边长为 0.75米的正方形花岗石的面积 3 怎样表示用x的代数式阴影部分的面积？ • 例1、一标志性建筑的 底面是正方形，在其四 周铺上花岗石，形成一 个宽为3米的正方形边 框，已知铺上这个边框 恰好用了192块边长为 0.75米的正方形花岗石， 问标志性建筑的底面边 长是多少米？ 3 X 3  24 3 3 0.75 0.75 192x     • 例1、一标志性建筑的 底面是正方形，在其四 周铺上花岗石，形成一 个宽为3米的正方形边 框，已知铺上这个边框 恰好用了192块边长为 0.75米的正方形花岗石， 问标志性建筑的底面边 长是多少米？ 3 X 3  4 3 3 0.75 0.75 192x     3 X 3 • 例1、一标志性建筑的 底面是正方形，在其四 周铺上花岗石，形成一 个宽为3米的正方形边 框，已知铺上这个边框 恰好用了192块边长为 0.75米的正方形花岗石， 问标志性建筑的底面边 长是多少米？  2 6 34 0.75 0.75 1922 x      3 X 3• 例1、一标志性建筑的 底面是正方形，在其四 周铺上花岗石，形成一 个宽为3米的正方形边 框，已知铺上这个边框 恰好用了192块边长为 0.75米的正方形花岗石， 问标志性建筑的底面边 长是多少米？  2 3 6 2 3 0.75 0.75 192x x       • 变式1、一标志性建筑的底 面是边长为6米正方形，在 其四周铺上花岗石，形成 一个宽为3米的正方形边框， 已知铺上这个边框恰好用 了192块正方形花岗石，问 每块正方形花岗石边长是 多少米？ 3 6 设每块正方形花岗石边长是x米,怎样根据等量关系列出方程？ 2 2 2192 12 6x   • 变式1、一标志性建 筑的底面是边长为6 米正方形，在其四 周铺上花岗石，形 成一个宽为3米的正 方形边框，已知铺 上这个边框恰好用 了x块边长为0.75米 的正方形花岗石， 求X是多少? 3 怎样根据等量关系列出方程？ 2 2 20.75 12 6x   小结： 1、列方程解决有关实际问题时，清楚 地分辨量之间的关系，尤其是等量关系 是建立方程的关键。解题中的检验对确 保答案的正确和合理很有帮助，但具体 过程可以不写。 2、对于等积变形问题，它的基本数量 关系是相关的面积公式，相等关系的特 征是存在不变量，也就是用不同的方法 来计算阴影部分的面积，面积不变。 例4 .学校组织植树活动,已 知在甲处植树的有23人,在 乙处植树的有17人.现调20 人去支援,使在甲处植树的 人数是乙处植树人数的2倍, 应调往甲,乙两处各多少人? 甲处 乙处 原有人数 增加人数 增加后人数 17+20-x23+x 20-xx 23 17 分析 设应调往甲处 x人,题目中所涉及 的有关数量及其关 系可以用右表表示: 甲处增加后人数=2×乙处增加后人数 想一想：如 果调往乙处 的人数为x， 方程应怎样 列? 在解决实际问题时,我们一般可以 通过分析实际问题, 抽象出数学问题, 然后运用数学思想方法解决问题.用列 表分析数量关系是常用的方法.