- 2021-05-12 发布 |
- 37.5 KB |
- 13页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级上数学课件八年级上册数学课件《角的平分线的性质》 人教新课标 (14)_人教新课标
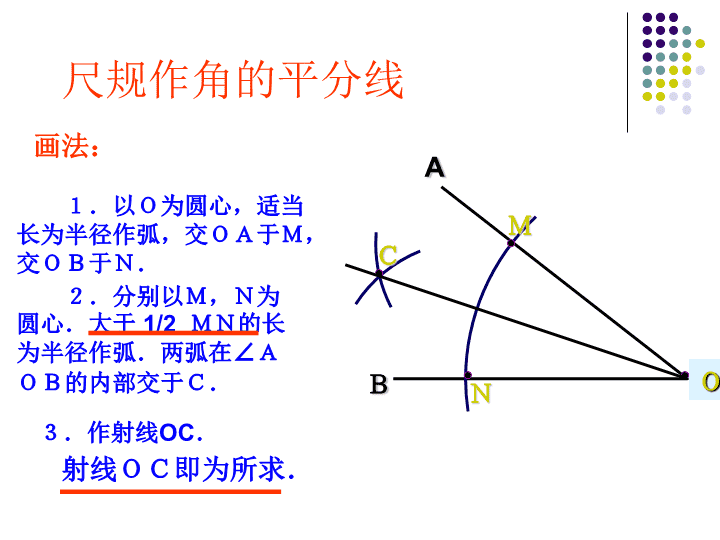
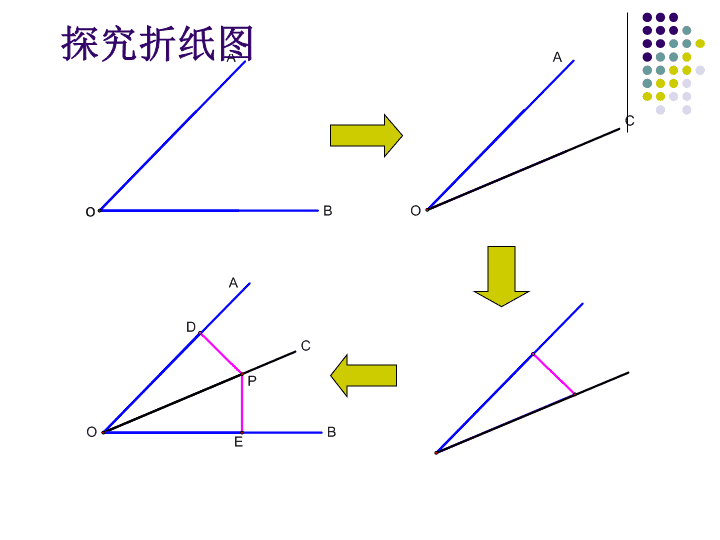
11.3角平分线的性质 尺规作角的平分线 画法: 1.以O为圆心,适当 长为半径作弧,交OA于M, 交OB于N. 2.分别以M,N为 圆心.大于 1/2 MN的长 为半径作弧.两弧在∠A OB的内部交于C. 3.作射线OC. 射线OC即为所求. A Bo A C O 探究折纸图 A C BE D O P 将AOB对折,在折出一个直角三角形(使第一条 折痕为斜边),然后展开,观察两次折叠形成的三 条折痕,你能得出什么结论? 可以看一看,第一条折痕是AOB的平分线OC,第 二次折叠形成的两条折痕PD,PE是角的平分线 上一点到AOB两边的距离,这两个距离相等. 折一折 . 角的平分线上的点到角的两边的距离相等 角的平分线的性质: O C B 1 A 2 P D E PD⊥OA,PE⊥OB ∴ PD=PE 用数学语言表述: 已知:如图,QD⊥OA,QE⊥OB, 点D、E为垂足,QD=QE. 求证:点Q在∠AOB的平分线上. 在角的内部,到角的两边的距离 相等的点在角的平分线上。 用数学语言表示为: 角的平分线上的点到角的两边的距离相等. 证明:过点P作PD 、PE、PF分别垂直于AB、 BC、CA,垂足为D、E、F ∵BM是△ABC的角平分线,点P在BM上 ∴PD=PE (在角平分线上的点到角的两边的距离相等) 同理 PE=PF. ∴ PD=PE=PF. 即点P到边AB、BC、 CA的距离相等 D E F A B C PMN 练习与思考: 1.要在S区建一个集贸市场,使它到公 路,铁路距离相等且离公路,铁路的交 叉处500米,应建在何处?(比例尺 1:20 000) S O 公路 铁路 2.如图,在△ABC中,D是BC的中点, DE⊥AB,DF⊥AC,垂足分别是E,F,且 BE=CF。 求证:AD是△ABC的角平分线。 A B C E F D 3.如图,△ABC的∠B的外角的平分线 BD与∠C的外角的平分线CE相交于点 P.求证:点P到三边AB,BC,CA 所在直线的距离相等. A B C D EPF G H B P 拓展与延伸 直线表示三条相互交叉的公路,现要建一 个货物中转站,要求它到三条公路的距离 相等,则可供选择的地址有:( ) A.一处 B. 两处 C.三处 D.四处 分析:由于没有限制在 何处选址,故要求的地 址共有四处。 1:画一个已知角的角平分线; 及画一条已知直线的垂线;2:角平分线的性质: 角的平分线上的点到角的两边的距离相 等.3:角平分线的判定结论: 到角的两边的距离相等的点在角平分线上。查看更多