八年级上数学课件八年级上册数学课件《三角形内角和定理的证明》 北师大版 (2)_北师大版

八年级上数学课件八年级上册数学课件《三角形内角和定理的证明》 北师大版 (2)_北师大版

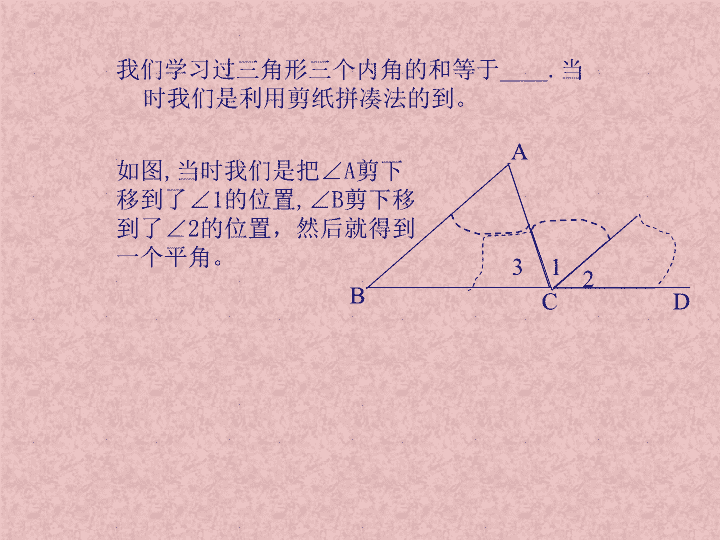
复习回顾 平行线的判定定理： ________角相等，两直线平行. ________角相等，两直线平行. ________角相等，两直线平行. 平行线的性质： 两直线平行， ________ 角相等. 两直线平行， ________ 角相等. 两直线平行， ________ 角互补. 我们学习过三角形三个内角的和等于____.当 时我们是利用剪纸拼凑法的到。 1 A B D 23 C 如图,当时我们是把∠A剪下 移到了∠1的位置,∠B剪下 移到了∠2的位置，然后就 得到一个平角。 7.5三角形内角和定理 学习目标 1、能掌握三角形内角和定理 2、会利用辅助线证题。 自学指导 利用3分钟时间学习课本178页证明过程思 考下列问题： 1.证明问题前怎样写已知求证。 2.题目中怎么作辅助线的？ 3.作辅助线需注意什么？ 4.题中主要用了哪些定理？ 检测： 在证明三角形内角和定理时,小明的想法是把三个角“凑” 到A处,他过点A作直线PQ∥BC(如图),他的想法可以吗?请 把你的证明过程写出来 证明:过点A作PQ∥BC,则 A B C ∠1=∠B(两直线平行,内错角相等), ∠2=∠C(两直线平行,内错角相等), 又∵∠1+∠2+∠3=1800 (平角的定义), ∴ ∠BAC+∠B+∠C=1800 (等量代换). 所作的辅助 线是证明的 一个重要组 成部分,要 在证明时首 先叙述出来. P Q 2 31 合作探究： 你还可以利用作平行线把三个角凑到其它 点来证明三角形内角和定理吗？以小组为 单位交流合作由C号画出你们的图形，并 由B号口述思路。 (1) A B CP Q R T S N (3) A B C PQ R M T S N (2) A B C PQ R M 三种语言表示：三角形内角和定 理 一、三角形三个内角的和等于1800. 二、△ABC中,∠A+∠B+∠C=1800. 三、几种变形: ∠A=1800 –(∠B+∠C). ∠B=1800 –(∠A+∠C). ∠C=1800 –(∠A+∠B). ∠A+∠B=1800-∠C. ∠B+∠C=1800-∠A. ∠A+∠C=1800-∠B. w这里的结论,以后可以直接运用. A B C 1.直角三角形的两锐角之和是多少度?画出图形写出已知求证 证明你的结论。C号 2.已知:如图在△ABC中，DE∥BC, ∠A=600, ∠C=700. 求证： ∠ADE=500. B号 D CB A E w结论: 直角三角形的两个锐角互余.以后可以直接 运用. 检测： 3.如图，已知△ABC中， ∠B 和 ∠C的平分线BE，CF交点O. 求证： ∠BOC=90°+ A B C E F O A 2 1 o掌握几何命题证明的方法,步骤, 格式及注意事项. o三角形内角和定理. o结论: 直角三角形的两个锐角互 余. 小结 拓展 知识的升华 独立 作业 习题7.6 1,2,3题; 祝你成功！